気柱共鳴

たとえば、試験管に口を近づけて息を吹き込むと音が出ます。
誰しも一度はやったことがある遊びではないでしょうか。
このような管を気柱とよびます。
気柱には大きく分けて 閉管 と 開管 があります。
今回はそれぞれについて詳しく解説をしていきます。
閉管
片側が閉鎖されている管です。
試験管などをイメージしてもらえばよいでしょう。
管の内部に生じる定常波ですが、
閉端は節、開端は腹になります。
以下、開端がきっちり腹とします。(一般には開口端補正として開端から腹が少し出ている・・・後述)
基本振動
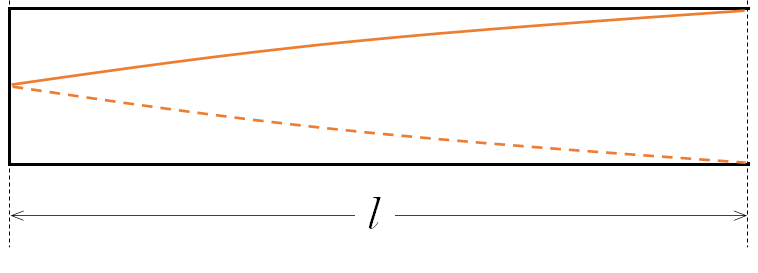
このとき、全長 $l$ のパイプとすると、波長 $\lambda$ は、 $\lambda = 4l$ になります。
なぜかというと、この定常波は、1波長のちょうど $\frac{1}{4}$ の形をしているからです(下図)。
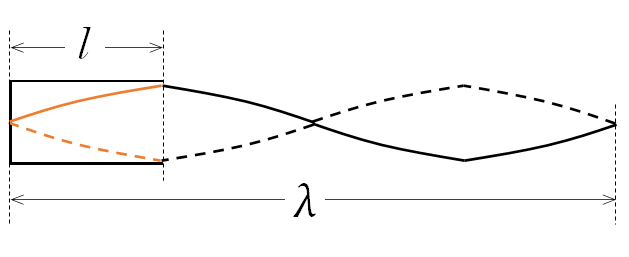
音速を $V$ 、振動数を $f_1$ とすると、
$f_1=\dfrac{V}{\lambda}=\dfrac{V}{4l}$
3倍振動
閉端が節、開端が腹となる、基本振動の次の振動は次のものしかありません。
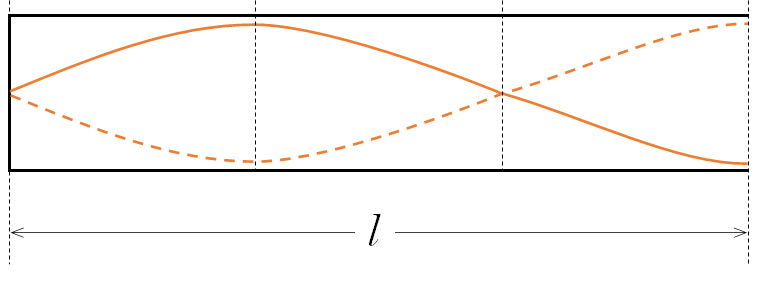
このとき、全長 $l$ のパイプとすると、波長 $\lambda$ は、 $\lambda = \dfrac{4}{3}l$ になります。
なぜかというと、この定常波は、1波長のちょうど $\frac{3}{4}$ の形をしているからです(下図)。

$l$ を3等分して4倍したら $\lambda$ になる・・・としてもよい
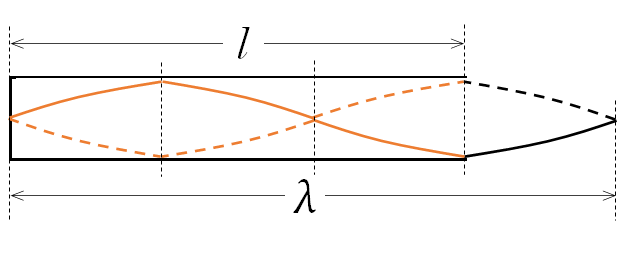
音速を $V$ 、振動数を $f_1$ とすると、 $\lambda = \dfrac{4}{3}l$ を代入して、
$f_3=\dfrac{V}{\lambda}=\dfrac{3V}{4l}$
これは、$f_1=\dfrac{V}{4l}$ を用いると、
$f_3=\dfrac{3V}{4l}=3 \times \dfrac{V}{4l}=3f_1$
この3倍の振動・・・というのが3倍振動と呼ばれるゆえんです。
5倍振動
まったく同様に考えて、次の定常波は図のようになります。
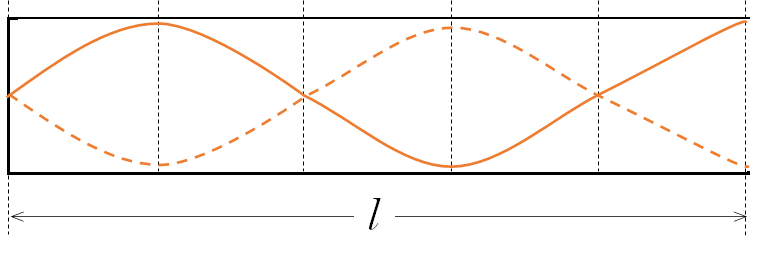
このとき、全長 $l$ のパイプとすると、波長 $\lambda$ は、 $\lambda = \dfrac{4}{5}l$ になります。
なぜかというと、この定常波の波長 $\lambda$ は、$l$ を5等分して4倍した長さだからです。下図
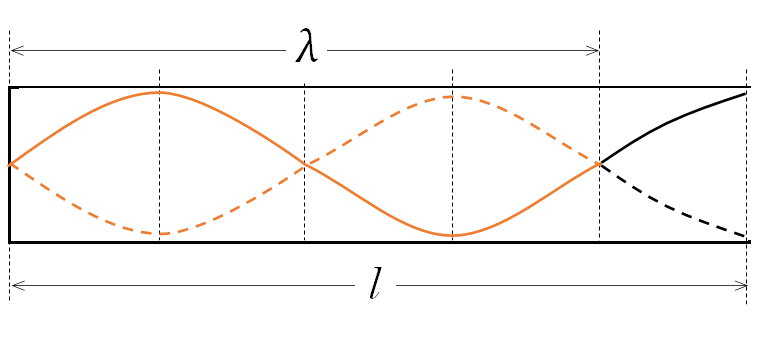
$f_5=\dfrac{V}{\lambda}=\dfrac{5V}{4l}$
これは、$f_1=\dfrac{V}{4l}$ を用いると、
$f_5=\dfrac{5V}{4l}=5 \times \dfrac{V}{4l}=5f_1$
この5倍の振動・・・というのが5倍振動と呼ばれるゆえんです。

こうしてみると閉管には偶数倍振動は存在しないことがわかりますね。
開管
両端とも開放されている管です。
開管の場合は両端がともに腹となる定常波を作ります。
基本振動
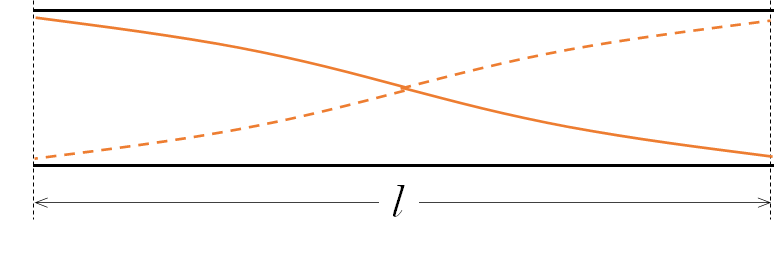
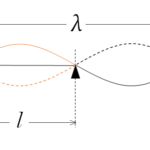
この場合、下図のように考えると
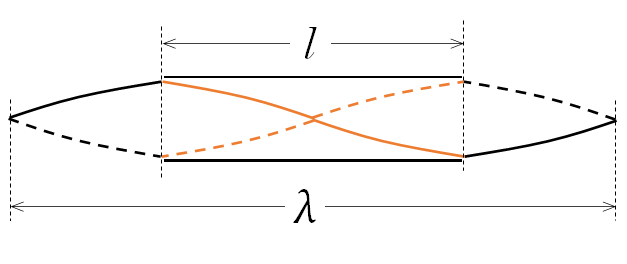
$\lambda=2l$
です。
したがって、基本振動の振動数 $f_1$ とすると、
$f_1 = \dfrac{V}{\lambda}=\dfrac{V}{2l}$
2倍振動
基本振動の次に考えられる定常波の状態は次のようになります。
必ず両端が腹になることに注意してください。
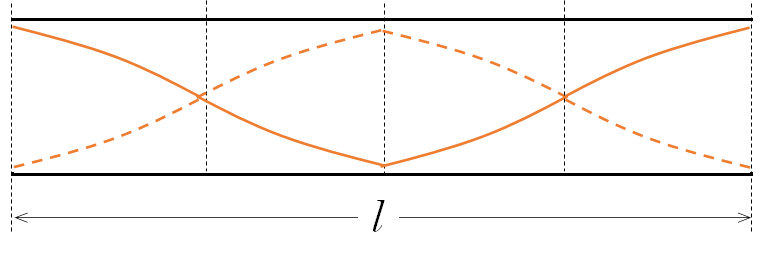
この場合、波長 $\lambda$ は、次の図から $\lambda=l$
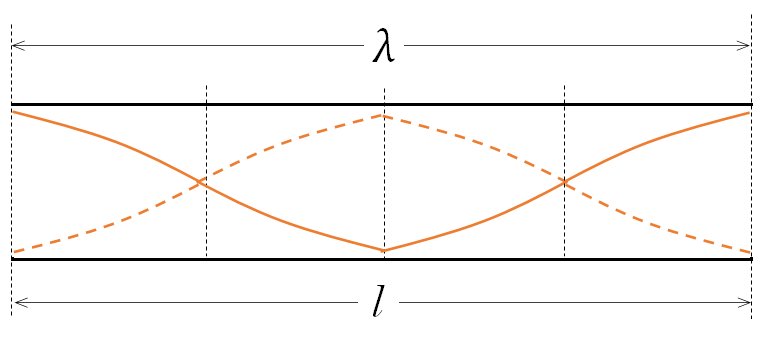
したがって、
$f_2 = \dfrac{V}{\lambda}=\dfrac{V}{l}=\dfrac{2V}{2l}$
$f_1 = \dfrac{V}{2l}$ であるから、
$f_2=\dfrac{2V}{2l}= 2 f_1$
3倍振動
さらに次の定常波は、
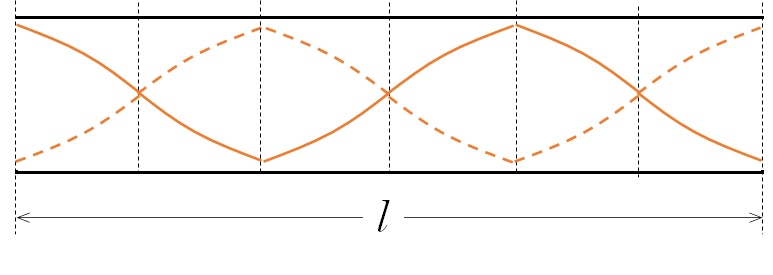
のようになります。
この場合、波長 $\lambda$ は、次の図から $\lambda=\dfrac{2}{3}l$

$\lambda$ は $l$ を 6等分して4倍した
つまり 3等分して2倍した・・・とも考えられます。
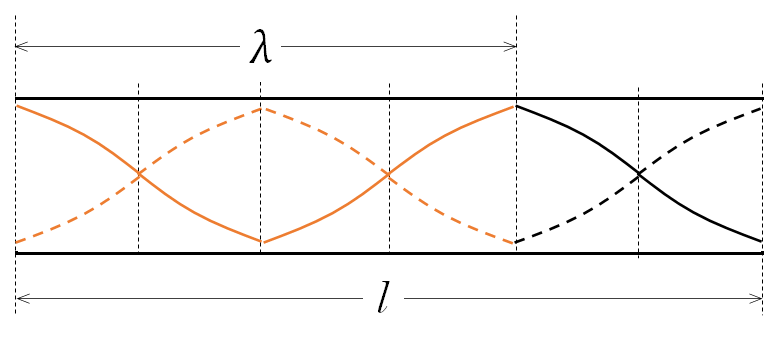
この時の振動数は
$f_3 = \dfrac{V}{\lambda}=\dfrac{3V}{2l}$
$f_1 = \dfrac{V}{2l}$ であるから、
$f_3=\dfrac{3V}{2l}= 3 f_1$
開口端補正
実際に実験をしてみると、開端から定常波の腹が少しはみ出てしまいます。
このはみ出た分を「開口端補正」といいます。
計算方法の一例
開口端補正 $d$ とすると、次の図から
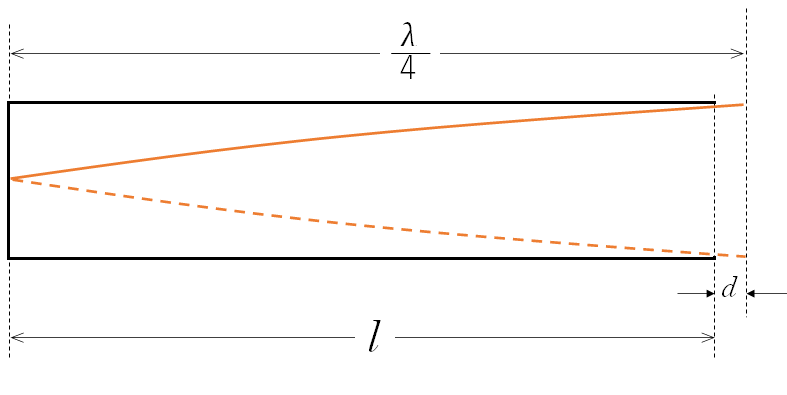
$\dfrac{\lambda}{4}=l + d$
が成り立ちます。
計算方法は状況によりいろいろですが、基本的にはこのよう考えればよいでしょう。




































コメント