この問題に関しては一度は考え方をマスターしておきましょう。
他にもいろいろ応用がきくようになります。
薄膜を含んだヤングの実験
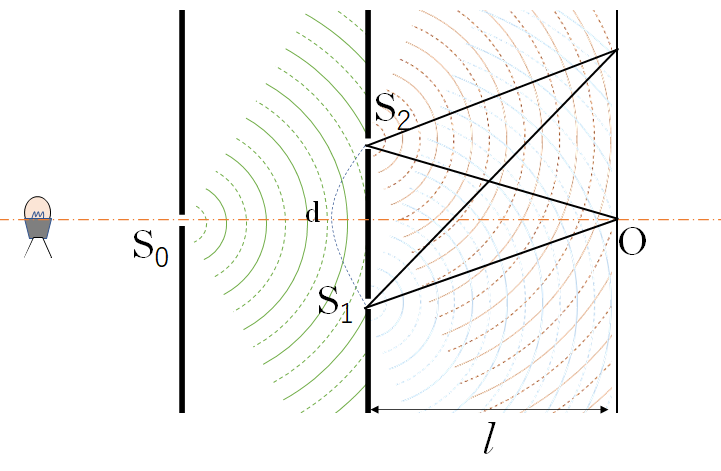
ヤングの実験
ヤングの実験とは二重スリットを通した光がスクリーン上で干渉縞を生じる現象です。
解説はこちら

今回はこのスリットの前に光を透過する薄膜(ガラスなど)を置いた場合について考えます。
スリットの前に薄膜を入れた場合
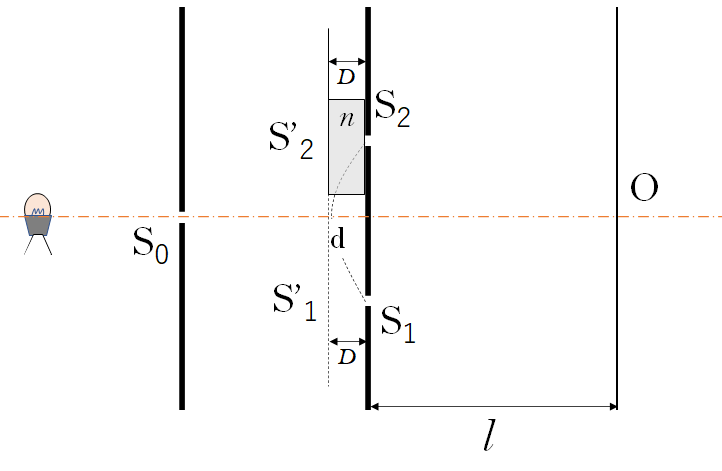
ヤングの実験において、2重スリットの片方に屈折率 $n$ で厚み $D$ の薄膜を入れます。
その場合、
- スクリーン上の中央の明線はどちらにずれるのか
- 中央の明線のずれの量 $x$ はいくらになるか
ということについて考えてみます。
解説
1. スクリーン上の明線はどちらへずれるのか
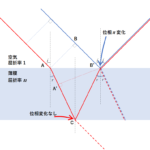
薄膜を挿入する前では、スクリーンの O が中央の明線が出るところです。
その場合、中央の O では、行路差 $\mathrm{\overline{S_1O}=\overline{S_2O}}$ となります。

そのため、各スリットを通った光はスクリーンの O 上で同位相となり強め合い明るくなるのです。
しかしここではスリットの手前に厚さ $D$ の薄膜を入れています。
そこで、起点を次の図のように薄膜の手前 $\mathrm{S’_1\:,\: S’_2}$ から考えることにします。
薄膜がない場合、それぞれの行路差 $\mathrm{\overline{S’_1S_1O}}$ と $\mathrm{\overline{S’_2S_2O}}$ の長さは同じです。
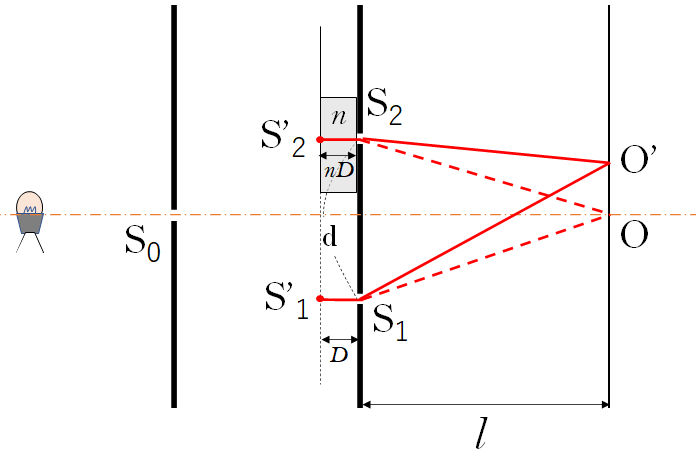
そうすると、薄膜を入れた場合、O がずれて O’ となったと考えるとき、
それぞれの光路差 $\mathrm{\overline{S’_1S_1O’}}$ と $\mathrm{\overline{S’_2S_2O’}}$ の長さは同じです。

行路差と光路差の違いは何でしょうか?
- 行路差・・・距離の差(経路差)
- 光路差・・・光学的距離を考慮に入れた差
薄膜の光学的距離を考慮に入れて光路差を考えます。
そうすると、薄膜の屈折率が $n$ のため、 $\mathrm{\overline{S’_1S_1}}=D$ および $\mathrm{\overline{S’_2S_2}}=nD$ です。
光学的距離では、
$\mathrm{\overline{S’_1S_1O’}} = \mathrm{\overline{S’_2S_2O’}}$
$\mathrm{\overline{S’_1S_1}} + \mathrm{\overline{S_1O’}} = \mathrm{\overline{S’_2S_2}} + \mathrm{\overline{S_2O’}}$
すなわち
$D+\mathrm{\overline{S_1O’}}=nD+\mathrm{\overline{S_2O’}}$
ここで、$n>1$ であるため、
$\mathrm{\overline{S_1O’}} > \mathrm{\overline{S_2O’}}$
となります。
したがって、O は図のように上にずれて O’ になります。

中央の明線のずれの量
次に、ずれの量を $x$ とします。光学的距離で考えて、
$\mathrm{\overline{S’_1S_1O’}} = \mathrm{\overline{S’_2S_2O’}}$
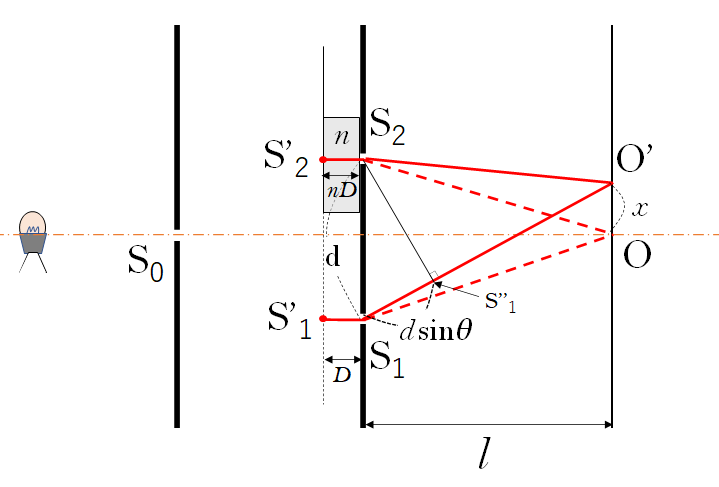
ですから、 $\mathrm{S_2}$ から $\mathrm{\overline{S_1O’}}$ におろした垂線の交点を $\mathrm{S^{\prime\prime}_1}$ とすると、ここで、角 $\theta$ が小さく、$l$ が $d$ に比べて十分大きければ、
$ \mathrm{\overline{S_2O’}}= \mathrm{\overline{S^{\prime\prime}_1O’}}$
と考えられるため、
$ \mathrm{\overline{S_2’S_2}}= \mathrm{\overline{S’_1S_1S^{\prime\prime}_1}}$
となります。
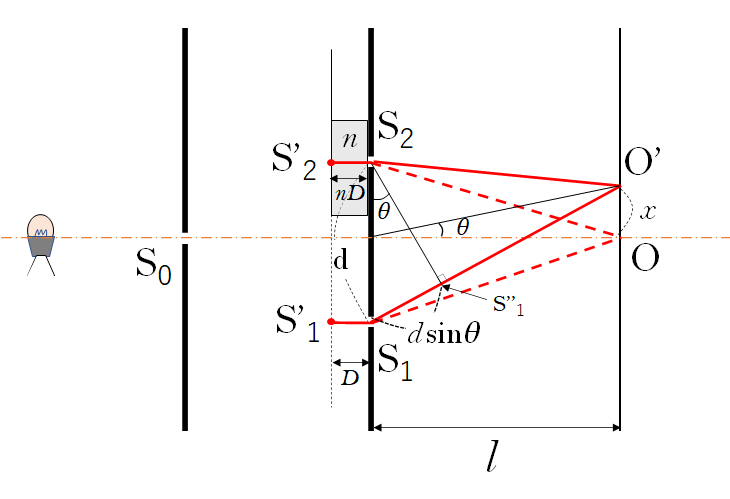
ここで図から、
$\mathrm{\overline{S_1S^{\prime\prime}_1}}=d\sin\theta$
と考えられるから、 $ \mathrm{\overline{S_2’S_2}}= \mathrm{\overline{S’_1S_1S^{\prime\prime}_1}}$ より、
$nD=D+d\sin\theta$
$\theta$ (ラジアン)が十分小さく、 $\sin\theta \fallingdotseq \tan\theta \fallingdotseq \theta$ とできるとき、
$\sin\theta \fallingdotseq \tan\theta \fallingdotseq \dfrac{x}{l}$

近似については、図から考えると次のようになります。
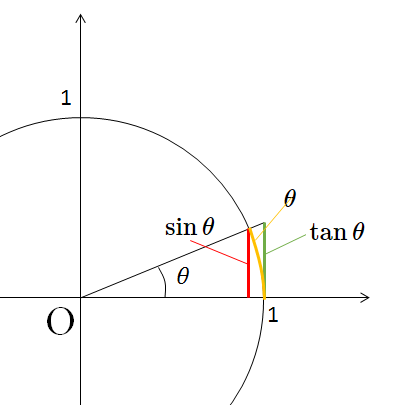
$\theta $ が十分小さいときは、
$\sin\theta \fallingdotseq \tan\theta \fallingdotseq \theta $
よって、
$nD = D+d\sin\theta = D + d\dfrac{x}{l}$
より、
$x=\dfrac{(n-1)Dl}{d}$
光学的距離
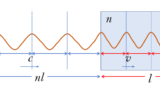
屈折率 $n$ の物質中の距離は真空中の $n$ 倍に相当します。
つまり、厚さ $D$ の薄膜(屈折率 $n$ )は真空中では $nD$ に相当します。光の場合、$n$ は必ず 1 より大きいため、$nD$ は必ず $D$ よりも大きくなります。

解説は次の記事を参考にしてください。
エッセンスの問題解説
物理のエッセンス55番に同じような問題があります。





































コメント