 物理のエッセンス
物理のエッセンス 物理のエッセンス 力学46番
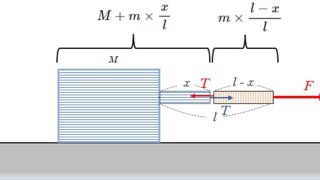
ロープの張力はどこでも同じ・・・として問題を解くことがほとんどです。でも、なぜロープ張力はどこでも同じなんでしょうか?それはロープや糸の質量を0としているからです。この問題ではロープの質量が無視できないとしています。
 物理のエッセンス
物理のエッセンス  物理のエッセンス
物理のエッセンス  力学
力学  力学
力学 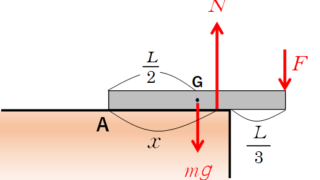 力学
力学  力学
力学 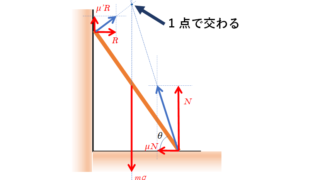 力学
力学 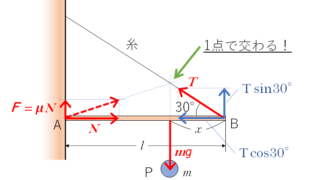 力学
力学 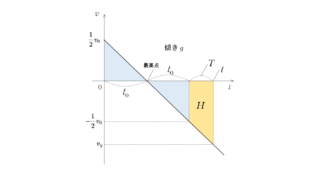 物理のエッセンス
物理のエッセンス  物理のエッセンス
物理のエッセンス  物理のエッセンス
物理のエッセンス  物理のエッセンス
物理のエッセンス  物理のエッセンス
物理のエッセンス 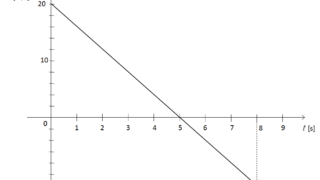 物理のエッセンス
物理のエッセンス 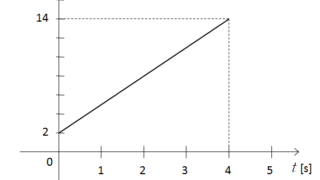 物理のエッセンス
物理のエッセンス 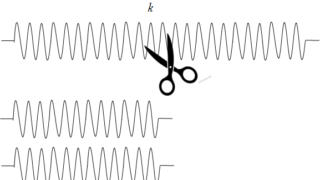 物理のエッセンス
物理のエッセンス 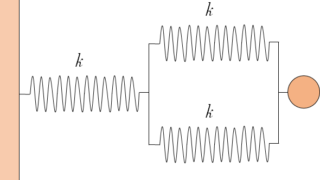 物理のエッセンス
物理のエッセンス 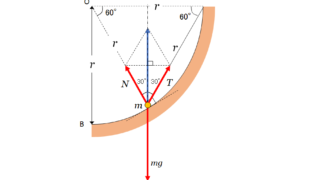 物理のエッセンス
物理のエッセンス  物理のエッセンス
物理のエッセンス  物理のエッセンス
物理のエッセンス