物理のエッセンス力学編4番
問題概要
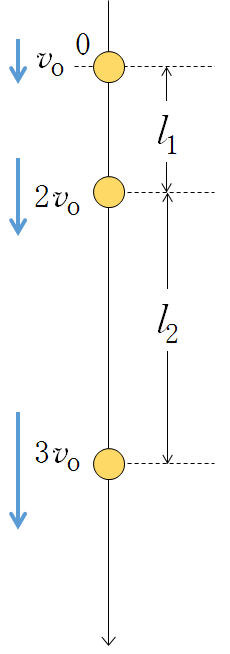 投げ下ろし運動において、
投げ下ろし運動において、
- 初速 $v_0$ が $2v_0$ になるまでの落下距離 $l_1$
- $2v_0$ から $3v_0$ になるまでの落下距離 $l_2$
として、$\dfrac{l_2}{l_1}$ を求めよ。重力加速度 $g$ とする。
式を用いるやり方は本の解答・解説にまかせて、ここでは $v-t$ グラフを用いて考えて見ましょう。
解説
$v-t$ 図を描いてみましょう。 もっと詳しく知りたい方、さらに応用したい方はこちらへ!
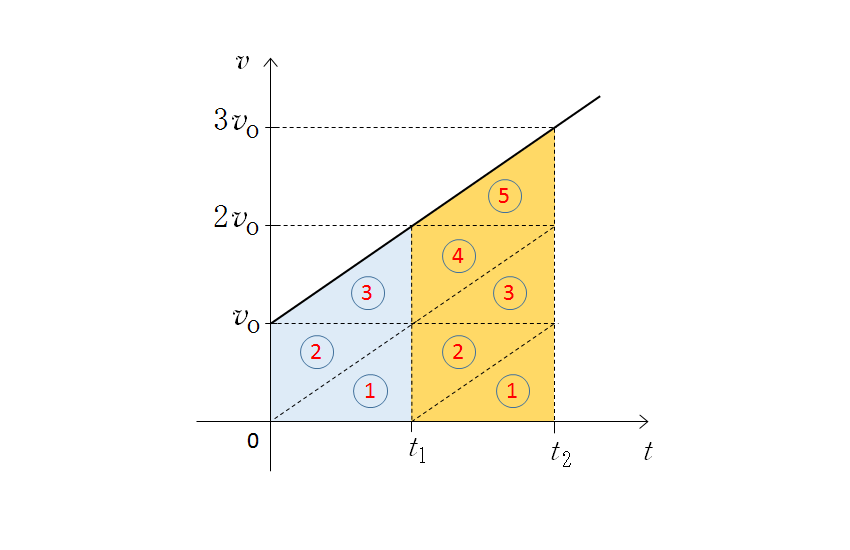
加速度は重力加速度 $g$ で一定だから、次の図のようになります。
時刻 $t_1$ と $t_2$ は適当でかまいません。
青い面積が $l_1$ 、オレンジの面積が $l_2$ を示しています。
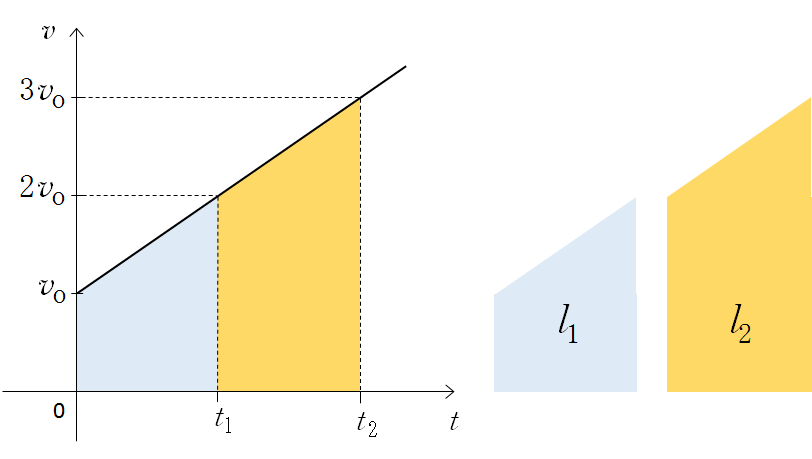

実はこれでもう解けたも同じです。
全く計算不要であることがお分かりでしょうか?
さて、次の図のように三角形で区切って見ます。
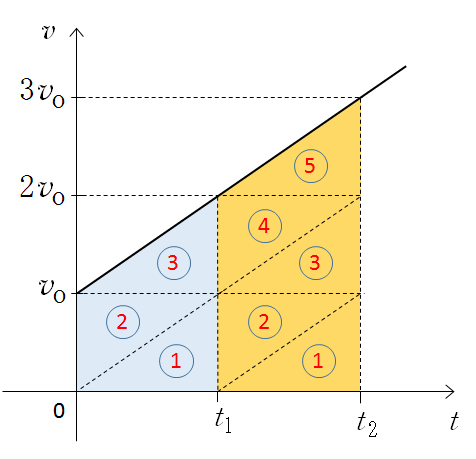
そうすると、全ての三角形は合同ですから、
当然、面積比(落下距離の比)は、
$\dfrac{l_2}{l_1}=\dfrac{5}{3}$
答え $\dfrac{l_2}{l_1}=\dfrac{5}{3}$

$v-t$ グラフは強力なツールです。
ぜひ使いこなしてください。
さらに高度な使い方はこちらへ
v-t グラフの活用 反発問題のテクニック解説
「落体の跳ね返りによる総運動時間を求める」という問題がありますが、$v-t$ グラフを使うことで簡単に解くこともできます。
ここではその方法や、$v-t$ グラフ一般について解説しています。















コメント