 電磁気
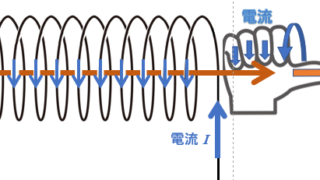
電磁気 直流電流の作る磁場
電磁気は力学とともに入試で非常に良く出る分野です。十二分に対策をしましょう。右手の法則や右ねじの法則、フレミングの左手則、レンツの規則などいろいろな法則や式が登場しますが、電磁気分野については、ある程度「公式」を覚えるという作業が必要になることは事実です。
 電磁気
電磁気 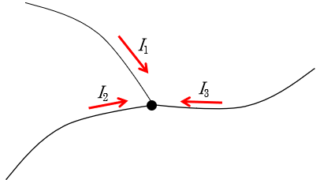 電磁気
電磁気 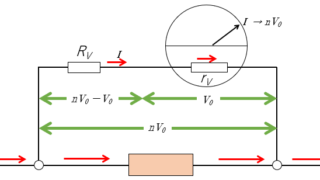 電磁気
電磁気 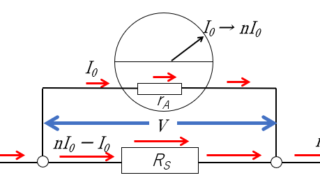 電磁気
電磁気  熱力学
熱力学 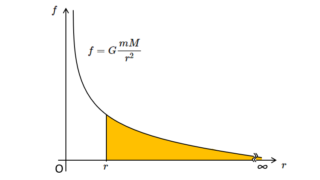 力学
力学  力学
力学 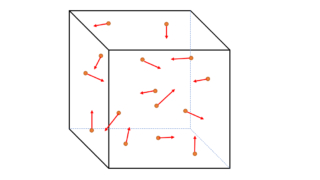 熱力学
熱力学 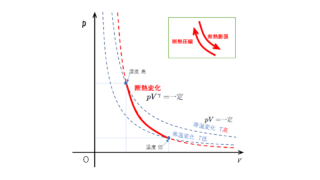 熱力学
熱力学 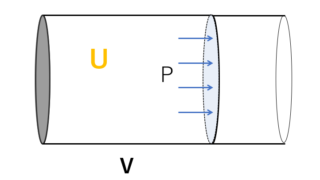 熱力学
熱力学 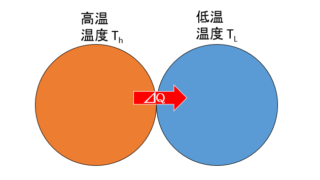 熱力学
熱力学 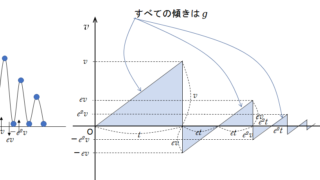 力学
力学 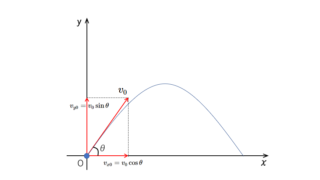 力学
力学  力学
力学 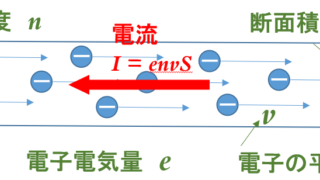 電磁気
電磁気 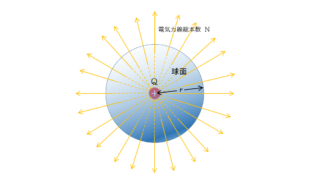 電磁気
電磁気  物理数学
物理数学  力学
力学 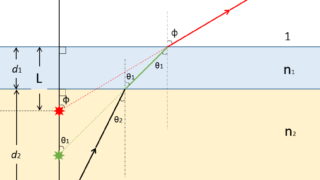 波動
波動  量子力学
量子力学