量子力学の巨人・シュレディンガーの発見した波動方程式を高校物理数学の範囲(ちょっとだけ逸脱しますが)でわかるように考えていきます。
まず1回目、方程式。
昔々習った教科書を見ながらすこしづつ思い出しつつ、なるべく高校生向けに書いていくつもりです。
ちょっと怪しいところのあるかもしれませんが、初心者に戻ってやりますので丁寧に式も書いていくつもりです。
間違っているときは、やさしくご指摘くださいませ。
高校物理でわかる量子力学 シュレディンガー方程式
力学・波動・電磁気・原子分野等の基本的な高校物理、および数学の初等的な知識を前提としています。
その都度、簡単な復習や解説をする予定ですが、踏み込んだ説明は別の記事に譲ります。
ド・ブロイ
ド・ブロイの提唱した物質波について

光子について、$c$ を光速としてエネルギーの式と、 $E=h\nu$ 運動量の式 $p=\dfrac{E}{c}$ より、運動量 $p$ は、
$p=\dfrac{E}{c}=\dfrac{h\nu}{c}$
で示される。
これに、波動の式、振動数 $\nu$ と 波長 $\lambda$ について、$c=\nu \lambda$ だから、
$p=\dfrac{h}{\lambda}$
となります。
ニュートン力学では、質量 $m$ をもつ物体が速さ $v$ で運動しているとき、その運動量は $p=mv$ で示されます。
ド・ブロイは $p=\dfrac{h}{\lambda}$ を物質である電子にも適用し、粒子の運動量 $p=mv$ を入れてみた。
すると、
$mv=\dfrac{h}{\lambda}$
$\lambda=\dfrac{h}{mv}$
となり、質量 $m$ の粒子のもつ波長 $\lambda$ が求められる。
この $\lambda$ をド・ブロイ波長といいます。
つまり、質量 $m$ 、速さ $v$ の粒子は、ド・ブロイ波長に相当する波を持っている?ということになります。
この波の正体は?・・・何だかよくわからないものは、さておき、ド・ブロイ波は、波動ですから、波動関数を考えることができるはずだ!と考えます。
追記:
ディラックの提唱した、ディラック$h$、$\hbar=\dfrac{h}{2\pi}$ を用いると、角振動数 $\omega=2\pi \nu$ 、波数 $k=\dfrac{2\pi}{\lambda}$ より、アインシュタイン=ド・ブロイの関係式が導かれます。
$E=h\nu=\hbar 2\pi \nu=\hbar \omega$
$p=\dfrac{h}{\lambda}=\dfrac{2\pi \hbar}{\lambda}=\hbar k$
この式を頭に入れておいて次にすすみましょう。
波動関数 $\Psi$
古典的な1次元の波動について、高等学校の教科書に載っている方法を考えます。
原点 $O$ が $y_0=A\sin \omega t$ で単振動しているとしましょう。
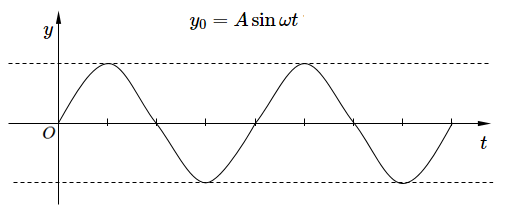
横軸 $t$ に注意してください。図は原点の振動のようすを示しています。
位置 $x$ の点の変位量 $y$ は、時間 $t’$ 前の原点振動に等しいから、
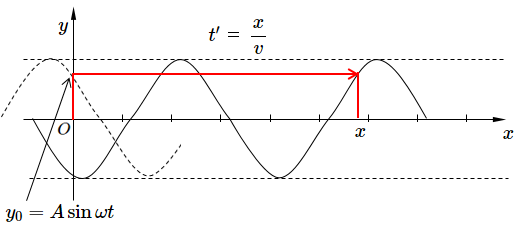
$y=A\sin\omega(t-t’)$
波の進行の速さを $v$ とすれば、 $t’=\dfrac{x}{v}$ なので、
$y=A\sin\omega(t-t’)$
$~~=A\sin\omega(t-\dfrac{x}{v})$
$~~=A\sin(\omega t -\dfrac{\omega x}{v})$
また、角振動数 $\omega=2\pi \nu$ 、波の速さ $v=\nu \lambda$ であるから、
$y=A\sin(\omega t -\dfrac{\omega x}{v})$
$~~=A\sin(\omega t -\dfrac{2\pi \nu x}{\nu \lambda})$
$~~=A\sin(\omega t -\dfrac{2\pi x}{\lambda})$
波数 $k=\dfrac{2\pi}{\lambda}$ を代入してやれば、
$~~=A\sin(\omega t -k x)$
として示されます。
このあたりのことは次の記事と動画にあります。


一般的な量子力学の解説本では
$y=A\sin(k x-\omega t )$
と $\sin$ の中身を入れ替えていることが多い。
この記事でも、以降はこちらの式を使います。
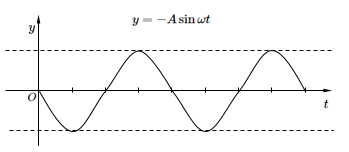
上の考え方で、はじめの原点振動を $y=-A\sin\omega t$ としてやれば同じように導けます。
$y=A\sin(\omega t -k x)=-A\sin(k x-\omega t )$ ですから、時刻 $t$ における変位量 $y$ が±違うだけですね。
波の進行方向は同じ向きです。
波は連続しているので、 $y=A\sin(k x-\omega t )$ であっても、$y=A\sin(\omega t -k x)$ であっても本質的には同じことです。
なぜ、このような形で $\sin$ の中身が違うのでしょうか?
それは、最初の導出のときの設定が違うからです。
上で説明したように、$x=0$ のときの原点振動を $y_0=f(t)=A\sin\omega t$ の形で示してやると高等学校で習う波の式が出ます。
しかし、 $t=0$ での波の形を $y_0=f(x)$ として考えてみてもかまわないわけですね。
そうすると、考える点線で示された波において、$x$ のところの変位量 $y$ は、$t$ 秒前の $y_0=f(x’)$ に等しくなります。
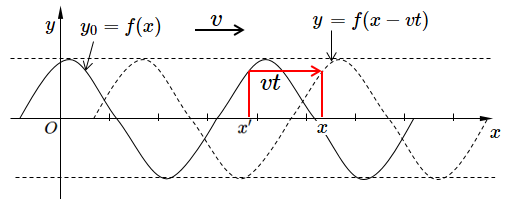
波は $t$ 秒間で $vt$ だけ進んだので、 $y=f(x’)=f(x-vt)$ として示されるものになります。
今、 $t=0$ での波の形を $y_0=A\sin 2\pi\dfrac{x}{\lambda} $ として考えてみます。(この式の $\sin$ の中身がこのようになることはいいでしょうか?)
そうすると、時刻 $t$ において、$x’$ のところの変位量 $y$ は、$t$ 秒前の $y_0$ に等しいので、 $y=f(x-vt)=A\sin 2\pi\dfrac{x-vt}{\lambda} $ として示されるものになります。(補足)
ここで、波数 $k=\dfrac{2\pi}{\lambda}$ 、 $v=\nu\lambda$ より、
$y=A\sin (2\pi\dfrac{x}{\lambda}-\dfrac{2\pi v}{\lambda}t)$
$~~=A\sin (kx-\dfrac{2\pi \nu \lambda}{\lambda}t)$
$~~=A\sin (kx-2\pi\nu t)$
ここで、 $\omega=2\pi\nu$ だから、
$y=A\sin (kx-\omega t)$
として一般的な波の式が得られます。
ここでオイラーの公式から(解説はこちらから)

$e^{ix}=\cos x+ i\sin x$
なので、
波動関数 $\Psi$ は便宜上、
$\Psi=Ae^{i(kx-\omega t)}$
$~~~=A\cos (kx-\omega t)+iA\sin(kx-\omega t)$
として、波動方程式は古典的にはこの実部や虚部をとるとすればよいですね。
三角関数の計算は面倒なことが多いので、交流などでは $e$ を使って計算し、最後にその実部や虚部を取ったりします。
$e^x$ の掛け算や微積などは三角関数の場合より比較的簡単です。
シュレディンガー方程式
古典的には、波動関数 $\Psi=Ae^{i(kx-\omega t)}$ の実部や虚部をとるというのは計算の便宜上のことにすぎないのです。
虚数の波などというのはちょっと想像できないですね。
しかし、量子力学で波動関数に虚数を含むことは本質的なことであると考えられています。
なぜか?については、後で考えることにして、とりあえず先にすすみましょう。
ここではまず1次元の波動方程式を考えます。
では、波動関数は虚数を含む
$\Psi=A\cos (kx-\omega t)+iA\sin(kx-\omega t)$
$~~~=Ae^{i(kx-\omega t)}$
としてやると、$\Psi$ を何度微分しても波動関数 $\Psi$ は形を変えずに残ります。
そして、微分することで指数部分の係数を自由に関数の外に出すことができるので、計算上非常に好都合です。
運動量
まず、量子的な運動量について考えます。
$p=\dfrac{h}{\lambda}=\hbar k$
$E=h\nu=\hbar \omega$
でした。
波動関数を $x$ で偏微分(補足参照)してみます。
この場合、たとえば $e^{ax}$ の微分を行うと $ae^{ax}$ と $x$ の係数が前に出てきます。
そこで、運動量 $p$ に関する式を得るため、 $Ae^{i(kx-\omega t)}$ を次のように書き換えてやります。ただし、 $k=\dfrac{p}{\hbar}$
$Ae^{i(kx-\omega t)}=Ae^{i(\frac{p}{\hbar}x-\omega t)}$
これを $x$ で偏微分すると、 $i\frac{p}{\hbar}$ が前に出てくることになります。
そして、 $Ae^{i(\frac{p}{\hbar}x-\omega t)}$ の部分に変化はありません。
こうしてやると、波動関数から運動量 $p$ に関する式を導くことができるのです。
やってみましょう。
$\Psi=Ae^{i(\frac{p}{\hbar}x-\omega t)}$
$\dfrac{\partial \Psi}{\partial x}=\dfrac{\partial }{\partial x}\{Ae^{i(\frac{p}{\hbar}x-\omega t)}\}$
$~~~~~~~=i\dfrac{p}{\hbar} \times A e^{i(\frac{p}{\hbar}x-\omega t)}$
$~~~~~~~=i\dfrac{p}{\hbar}\Psi$
より、
$\dfrac{\hbar}{i} \dfrac{\partial}{\partial x} \Psi=p\Psi$
この式の意味するところは、波動関数 $\Psi$ に $\dfrac{\hbar}{i} \dfrac{\partial}{\partial x} $ という演算を仕掛けると、右辺にあるように、運動量を波動関数にかけたものが出てくるということになります。
この $\hat{p} \rightarrow \dfrac{\hbar}{i} \dfrac{\partial}{\partial x}$ 、$\hat{p}$ を運動量演算子とよびます。
$\hat{p}$ の意味は、偏微分を仕掛ける演算子という意味です。普通の掛け算と混同しないようにしてください。
普通の $p$ と紛らわしいので、^ をつけて区別しています。
運動エネルギー
次は運動エネルギーについてです。$p=\dfrac{h}{\lambda}=\hbar k$ でした。
運動エネルギーは、質量 $m$、速さ $v$ としたときに、 $T=\dfrac{1}{2}mv^2$ と示されます。
これは、 $p=mv$ という関係を使うと $T=\dfrac{p^2}{2m}$ となります。
より、$p^2=2mT$
先程の式、 $\dfrac{\hbar}{i} \dfrac{\partial}{\partial x} \Psi=p\Psi$ を、もう一度 $\dfrac{\partial }{\partial x}$ してみます。
そうすると、もう一度 $p$ が出てくるため、$p^2$ という係数が出ることになります。
したがって、運動エネルギー $T=\dfrac{p^2}{2m}$ に関する式を出すことができるのです。
早速やってみましょう。
$\dfrac{\partial}{\partial x}\left(\dfrac{\hbar}{i} \dfrac{\partial}{\partial x} \Psi\right)=\dfrac{\partial}{\partial x}\left(p\Psi\right)$
$\dfrac{\hbar}{i}\dfrac{{\partial}^2}{{\partial x}^2}\Psi=p\dfrac{\partial}{\partial x} \Psi$
ここで、 $\dfrac{\hbar}{i} \dfrac{\partial}{\partial x} \Psi=p\Psi$ より、 $\dfrac{\partial}{\partial x} \Psi=i\dfrac{p}{\hbar}\Psi$ だから、
$\dfrac{\hbar}{i}\dfrac{{\partial}^2}{{\partial x}^2}\Psi=i\dfrac{p^2}{\hbar}\Psi$
ここで、 $p^2=2mT$ であるから、
$\dfrac{\hbar}{i}\dfrac{{\partial}^2}{{\partial x}^2}\Psi=i\dfrac{2mT}{\hbar}\Psi$
ゆえに、
$-\dfrac{\hbar^2}{2m}\dfrac{{\partial}^2}{{\partial x}^2}\Psi=T\Psi$
これは、波動関数 $\Psi$ に $-\dfrac{{\hbar}^2}{2m}\dfrac{{\partial}^2}{{\partial x}^2}$ を仕掛けると、$T\Psi$ すなわち、運動エネルギー×波動関数 になることを意味しています。
エネルギー
次はエネルギーに関する関係を考えます。
$\Psi=Ae^{i(kx-\omega t)}$ を $E=\hbar \omega$ で変形します。
$\omega=\dfrac{E}{\hbar}$ だから、
$\Psi=Ae^{i(kx-\omega t)}=Ae^{i(kx-\frac{E}{\hbar} t)}$
となります。
時間で偏微分 $\dfrac{\partial}{\partial t}$ しましょう。
そうすると今度はすぐに $E$ が出てきます。
$\dfrac{\partial}{\partial t}\Psi=\dfrac{\partial}{\partial t}\{Ae^{i(kx-\frac{E}{\hbar} t)}\}$
$\dfrac{\partial}{\partial t}\Psi=-i\dfrac{E}{\hbar}Ae^{i(kx-\frac{E}{\hbar} t)}$
ここで、 $\Psi=Ae^{i(kx-\frac{E}{\hbar} t)}$ だから、
$\dfrac{\partial}{\partial t}\Psi=-i\dfrac{E}{\hbar} \Psi$
より、
$i\hbar\dfrac{\partial}{\partial t}\Psi=E\Psi$
シュレディンガー方程式

さて、エネルギー $E$ は $E=運動エネルギー + 位置エネルギー=T+V$ ですね。
運動エネルギーに関しては、上にあげたように $-\dfrac{{\hbar}^2}{2m}\dfrac{{\partial}^2}{{\partial x}^2}\Psi=T\Psi$ で示されます。
また、 $i\hbar\dfrac{\partial}{\partial t}\Psi=E\Psi$ ですから、
$T+V=E$
$T\Psi+V\Psi=E\Psi$
$-\dfrac{{\hbar}^2}{2m}\dfrac{{\partial}^2}{{\partial x}^2}\Psi+V\Psi=i\hbar\dfrac{\partial}{\partial t}\Psi$
$\left(-\dfrac{{\hbar}^2}{2m}\dfrac{{\partial}^2}{{\partial x}^2}+V\right)\Psi=i\hbar\dfrac{\partial}{\partial t}\Psi$
これをシュレディンガー方程式と呼びます。
この演算子、 $\left(-\dfrac{{\hbar}^2}{2m}\dfrac{{\partial}^2}{{\partial x}^2}+V\right)$ を $\hat{H}$ とし、ハミルトニアンと呼びます。
おさらいです
波動関数 $\Psi$ に $\dfrac{\hbar}{i} \dfrac{\partial}{\partial x} $ という演算を仕掛けると、運動量を波動関数にかけたものが出てくる。
運動量演算子
$\dfrac{\hbar}{i} \dfrac{\partial}{\partial x} \Psi=p\Psi$
波動関数 $\Psi$ に $-\dfrac{{\hbar}^2}{2m}\dfrac{{\partial}^2}{{\partial x}^2}$ を仕掛けると、 $T\Psi$ すなわち、 運動エネルギー×波動関数 になる。
$-\dfrac{{\hbar}^2}{2m}\dfrac{{\partial}^2}{{\partial x}^2}\Psi=T\Psi$
また、波動関数 $\Psi$ を時間で偏微分 $\dfrac{\partial}{\partial t } \Psi$ すると、
$i\hbar\dfrac{\partial}{\partial t}\Psi=E\Psi$
以上より、
$\left(-\dfrac{{\hbar}^2}{2m}\dfrac{{\partial}^2}{{\partial x}^2}+V\right)\Psi=i\hbar\dfrac{\partial}{\partial t}\Psi$
ハミルトニアン $\hat{H} \equiv -\dfrac{{\hbar}^2}{2m}\dfrac{{\partial}^2}{{\partial x}^2}+V$
補足
$t=0$ において、波は図のように $\sin$ 関数とすると、原点の振動は時間に対して $-\sin$ の形の関数になるのがわかると思います。
波のグラフ $t=0$
$y=A\sin kx$
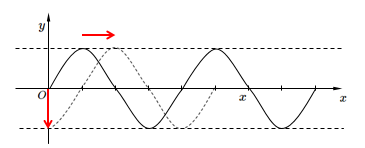
原点の振動 $x=0$ (横軸は $t$ )
$y=-A\sin \omega t$
偏微分

ここで、偏微分について簡単に解説します。
いずれ別記事で詳しく解説するつもりです。
例えば、$f(x,y)$ で示される2変数関数を、$y$ を定数とみなして $x$ で微分することを $f(x,y)$ を$x$ で偏微分するといいます。
記号は、 $\dfrac{\partial f(x,y)}{\partial x}$ と書きます。
例題をやってみましょう。
$f(x,y)=3x^2+4xy+y^2$
を $x$ で偏微分します。
$\dfrac{\partial f(x,y)}{\partial x}=6x+4y$
ですね。つまり、 $y$ を定数と考えて $x$ で微分するだけです。
偏微分の意味ですが、 $z=f(x,y)$ してグラフを考えてみます。
その場合に $x$ で偏微分するとは、平面の $x$ 軸方向の傾きを考えるということになります。
また、$y$ で偏微分すると、平面の $y$ 軸方向の傾きを考えるということになります。
複素数の計算 指数の掛け算は三角関数の足し算
複素平面
$z=a+ib$
$r=|z|=|a+ib|=\sqrt{(a^2+b^2)}$
複素平面(図)の原点からの距離 $r$ は、 $(a+ib)(a-ib)$ で示される。
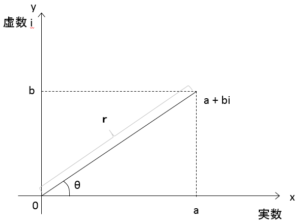
$a+ib$ の複素共役は $a-ib$
$(a+ib)(a-ib)=a^2-i^2b^2=a^2+b^2$
$r=\sqrt{(a^2+b^2)}$
複素数と指数の関係
$e^{i\alpha}=\cos \alpha +i \sin \alpha$
$e^{i\beta}=\cos \beta +i \sin \beta$
$e^{i\alpha}e^{i\beta}=e^{i(\alpha + \beta)}=\cos(\alpha + \beta)+i\sin(\alpha + \beta)$
$e^{ix}$ の掛け算は三角関数では足し算に変換される
このことについては次の記事参照












コメント