極形式の計算とオイラーの公式の関係

極形式の計算とオイラーの公式の関係

極形式の計算とオイラーの公式の関係

オイラーの公式

$e^{i\theta}=\cos\theta+i\sin\theta$

をつかって極形式の計算をしてみます。

これが使えると三角関数の面倒くさい計算をしなくても済みます。

高校数学でわかる！オイラーの公式を導こう

オイラーの公式人類の至宝とも呼ばれるオイラーの等式今回は「オイラーの公式」を導いた上で、「オイラーの等式」を確かめてみましょう。

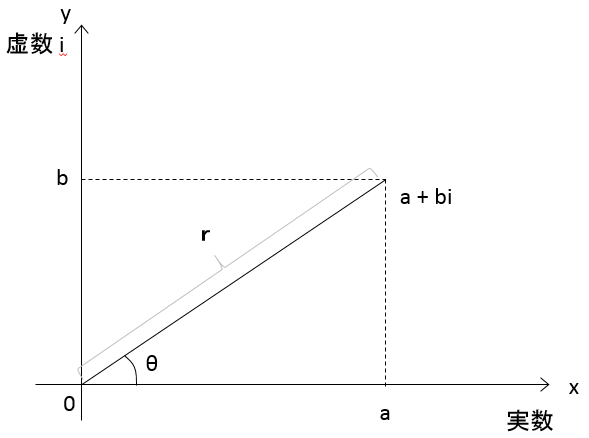
極形式とは

極形式とは、

$a+bi=r(\cos\theta+i\sin\theta)$

の形式で示すことです。($r>0$)

この $\theta$ を $\theta=\arg z$ とし、偏角といいます。

例題

例題1

次の複素数を極形式で示せ

$\alpha=1+i$　、　$\beta=1+\sqrt{3}i$

答え

複素数平面を描いてみましょう。

そうすると、図のようになります。

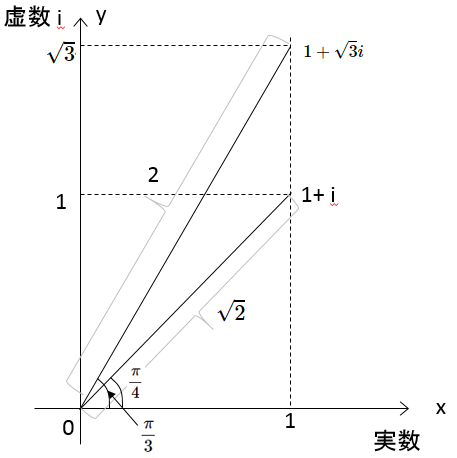
$\arg \alpha=\dfrac{\pi}{4}$ 、$r=\sqrt{2}$ だから、

$\alpha=1+i=\sqrt{2}(\cos\dfrac{\pi}{4}+i\sin\dfrac{\pi}{4})$

$\arg \beta=\dfrac{\pi}{3}$ 、$r=2$ だから、

$\beta=1+\sqrt{3}i=2(\cos\dfrac{\pi}{3}+i\sin\dfrac{\pi}{3})$

例題2

例題1の $\alpha \beta$ と、$\dfrac{\alpha}{\beta}$ について極形式で示せ。

答え

\begin{eqnarray}
\alpha \beta&=&\sqrt{2}\left(\cos\dfrac{\pi}{4}+i\sin\dfrac{\pi}{4}\right)\times 2\left(\cos\dfrac{\pi}{3}+i\sin\dfrac{\pi}{3}\right)\\\\
&=&2\sqrt{2}\left(\cos\dfrac{\pi}{4}\cos\dfrac{\pi}{3}+i\sin\dfrac{\pi}{4}\cos\dfrac{\pi}{3}+i\sin\dfrac{\pi}{3}\cos\dfrac{\pi}{4}-\sin\dfrac{\pi}{4}\sin\dfrac{\pi}{3}\right)\\\\
&=&2\sqrt{2}\left\{\left(\cos\dfrac{\pi}{4}\cos\dfrac{\pi}{3}-\sin\dfrac{\pi}{4}\sin\dfrac{\pi}{3}\right)+i\left(\sin\dfrac{\pi}{4}\cos\dfrac{\pi}{3}+\sin\dfrac{\pi}{3}\cos\dfrac{\pi}{4}\right)\right\}\\\\
&=&2\sqrt{2}\left\{\cos(\dfrac{\pi}{4}+\dfrac{\pi}{3})+i(\sin(\dfrac{\pi}{4}+\dfrac{\pi}{3}))\right\}\\\\
&=&2\sqrt{2}\left(\cos\dfrac{7\pi}{12}+i\sin\dfrac{7\pi}{12}\right)
\end{eqnarray}

ちょっと面倒ですね。

これをオイラーの式を使って書き直しましょう。

$\alpha=1+i=\sqrt{2}(\cos\dfrac{\pi}{4}+i\sin\dfrac{\pi}{4})=\sqrt{2}e^{i\frac{\pi}{4}}$

$\beta=1+\sqrt{3}i=2(\cos\dfrac{\pi}{3}+i\sin\dfrac{\pi}{3})=2e^{i\frac{\pi}{3}}$

したがって、

\begin{eqnarray}
\alpha\beta&=&\sqrt{2}e^{i\frac{\pi}{4}}\cdot 2e^{i\frac{\pi}{3}}\\\\
&=&2\sqrt{2}e^{i(\frac{\pi}{4}+\frac{\pi}{3})}\\\\
&=&2\sqrt{2}e^{i\frac{7\pi}{12}}\\\\
&=&2\sqrt{2}\left(\cos\dfrac{7\pi}{12}+i\sin\dfrac{7\pi}{12}\right)
\end{eqnarray}

どうです？簡単ですね。
$\dfrac{\alpha}{\beta}$ も同じようにやってみると、

\begin{eqnarray}
\dfrac{\alpha}{\beta}&=&\dfrac{\sqrt{2}e^{i\frac{\pi}{4}}}{2e^{i\frac{\pi}{3}}}\\\\
&=&\dfrac{\sqrt{2}}{2}e^{i(\frac{\pi}{4}-\frac{\pi}{3})}\\\\
&=&\dfrac{\sqrt{2}}{2}e^{-i\frac{\pi}{12}}\\\\
&=&\dfrac{\sqrt{2}}{2}\left(\cos\dfrac{-1}{12}\pi+i\sin\dfrac{-1}{12}\pi\right)
\end{eqnarray}