16世紀、ポーランドのコペルニクス(1473 – 1543)は、当時主流であった天動説に対し、地動説を唱えた。
その後、デンマークのティコ・ブラーエ(1546 – 1601)の助手(研究仲間?)になった、ドイツのヨハネス・ケプラー(1571 – 1630)はティコ・ブラーエの残した膨大な観測資料をもとに、ケプラーの法則を発見した。
ケプラーの法則
- 第1法則 楕円軌道の法則 惑星は太陽を一つの焦点とする楕円軌道上を運動する
- 第2法則 面積速度一定の法則 太陽と惑星を結ぶ線分が一定時間に通過する面積は一定
- 第3法則 公転周期の法則 惑星の公転周期 $T$ の $2$ 乗と楕円の長半径 $a$ の $3$ 乗の比は一定 $\frac{T^2}{a^3}=一定$
ケプラーの第1法則
楕円は、2つの点(楕円の焦点)からの距離の和が一定であるような曲線です。
簡単な描き方は、例えば決まった点にピンを立てて糸を結びます。
そして、鉛筆で、糸をたるまないようにしながら引っ張って曲線をかけば出来上がりです。
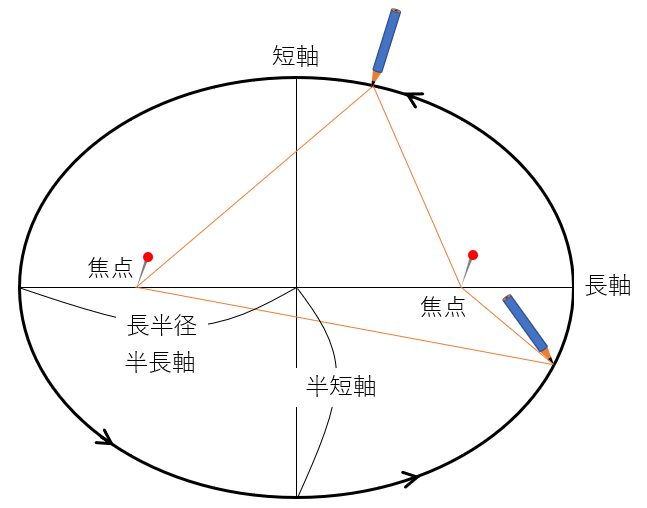
このとき、ケプラーの第 3 法則で使われる「長半径」とは、楕円を縦横にスパッと切った時の図の横方向(半長軸)の長さを言います。
ケプラーの第1法則によれば、惑星はこの焦点の一つを中心として、楕円軌道上を運動しています。
この惑星の回転スピードは一定ではなく、その速さは次の第 2 法則「面積速度一定の法則」に従います。
ケプラーの第2法則
ニュートンはその著書「プリンキピア」の中で、運動の第2法則と幾何学的方法を用いて、ケプラーの第2法則「面積速度一定の法則」を説明しています。詳しくはリンクをご覧ください。
そこから導かれる、角運動量保存則を考えれば、なぜフィギュアスケートのスピンが速くなるのか?の答えがわかります。
面積速度一定の法則では、図にあるように一定時間に太陽(焦点)と惑星を結ぶ線(動径)が単位時間に通過する面積 $\Delta S$ が等しくなります。
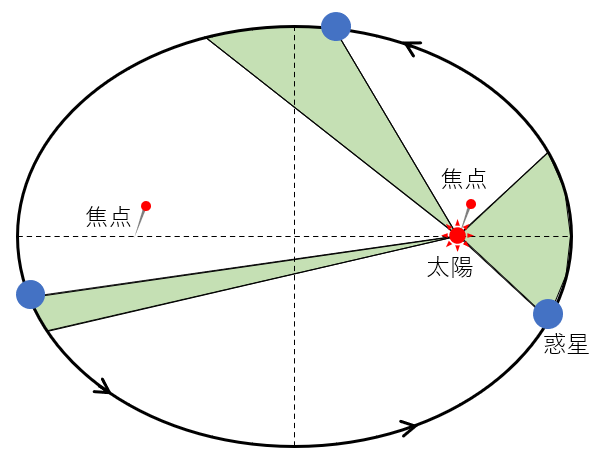
$\dfrac{\Delta S}{\Delta t}=一定$ です。
ケプラーの第3法則
惑星の公転周期 $T$ の 2 乗と楕円の長半径 $a$ の 3 乗は次の式を満たします。
$\dfrac{T^2}{a^3}=k \:\:\:\:\:\:一定$
地球と太陽だけでなく、太陽を焦点としているすべての惑星について $k$ は同じ値をとり、一定です。
これは、太陽質量を $M$ 、惑星質量を $m$、簡単のため軌道を円軌道と仮定し、回転半径を $r$ とします。 $G$ : 万有引力定数、$\omega$ : 各速度、$T$ : 周期
慣性力である遠心力と万有引力のつり合いの式を立ててみると、
$mr\omega^2=mr\left( \dfrac{2 \pi}{T}\right)=G\dfrac{mM}{r^2}$
とすれば、これを変形して、
$\dfrac{T^2}{r^3}=\dfrac{4\pi^2}{GM}$
としたとき、左辺はケプラーの第 3 法則を示しています。
右辺の $\dfrac{4\pi^2}{GM}$ の値は、太陽の質量 $M$ に関係し、惑星の質量 $m$ や種類には無関係に一定であることがわかります。
ハレー彗星

ハレー彗星は太陽を一つの焦点とする大きな楕円軌道上を運動します。
この楕円軌道の長半径 $a$ を 18 天文単位(注)とすると、ハレー彗星の公転周期を求めることができます。(注:1天文単位は地球-太陽 間の平均距離とします)
地球と太陽の距離を 1.0 天文単位、地球の公転周期を 1.0 年とします。
そうすると、$\dfrac{T^2}{a^3}=k \:\:\:\:\:\:一定$ より
- 地球 : $\dfrac{1.0^2}{1.0^3}=k$
- ハレー彗星 : $\dfrac{T^2}{18^3}=k$
どちらも太陽を公転の中心としていますから、$k$ の値は同じです。
したがって、 $\dfrac{1.0^2}{1.0^3}=\dfrac{T^2}{18^3}$ より、
$T=\sqrt{18^3}=18\sqrt{18}=18\times 3 \sqrt{2}\fallingdotseq 76\:\:\:\:\:年$
となります。
もう少し精密な計算によると、ハレー彗星の公転周期は約 75.3 年です。
そして、前回のハレー彗星は1986年2月に観測されており、次回は2061年夏頃に出現すると考えられています。
エドモンド・ハレー(イギリス 1656 – 1742)は、このハレー彗星の周期性に気がつき、計算により次の出現時期を予想したのですが、みずから予想したすい星(1759年出現)を見る前に没しています。

ハレー本人もさぞかし見たかったでしょうね。
ハレーは当時としては比較的長命ですが、
生きていれば、1759年には103歳になりますね。

Thomas Murray – uploaded from http://www.phys.uu.nl/~vgent/astrology/newton.htmoriginally uploaded on en.wikipedia by Lumos3 (トーク · 投稿記録) at 2005年12月19日, 13:46. Filename was Edmund Halley.gif., パブリック・ドメイン, https://commons.wikimedia.org/w/index.php?curid=3504947による




































コメント
とても参考になりました。ありがとうございます。しかし一つ指摘させていただくなら、ハレー彗星は太陽に近づくにつれその氷の昇華により核から宇宙ゴミを噴出する力が働いてしまうため厳密にはケプラーの第三法則に従わないようです。
コメントありがとうございます。
なるほど、ですね。