 電磁気
電磁気 電磁誘導
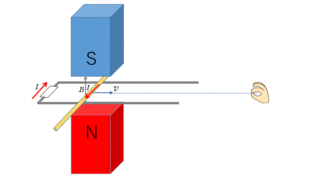
コイルに対して磁石を動かす、磁石に対してコイルを動かす・・・・こういう場合にコイルには起電力が生じ、回路を作ってやると誘導電流が流れます。または磁場中で導体棒を動かすときも誘導起電力が生じます。今回は、電磁誘導について解説します。
 電磁気
電磁気 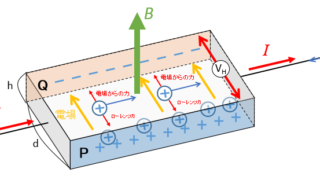 電磁気
電磁気  電磁気
電磁気 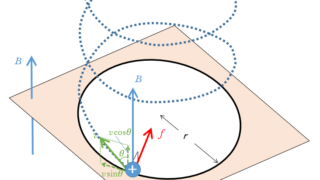 電磁気
電磁気 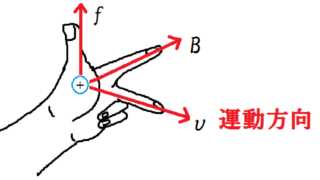 電磁気
電磁気 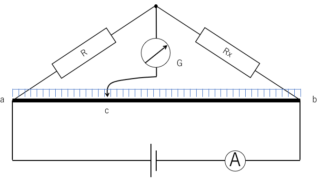 電磁気
電磁気 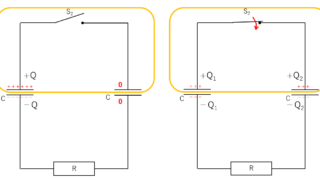 電磁気
電磁気 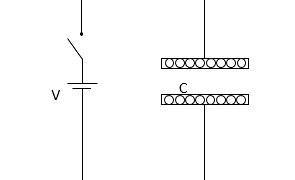 電磁気
電磁気 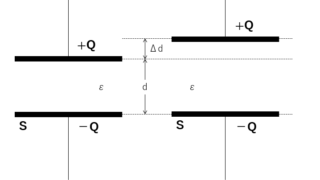 電磁気
電磁気 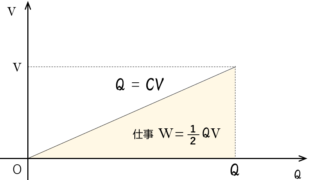 電磁気
電磁気  電磁気
電磁気 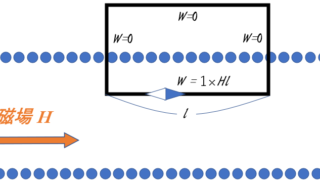 電磁気
電磁気 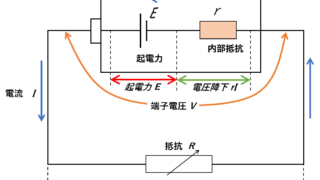 電磁気
電磁気 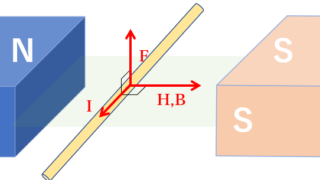 電磁気
電磁気 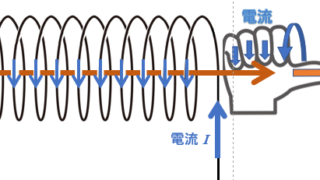 電磁気
電磁気 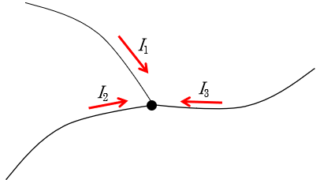 電磁気
電磁気 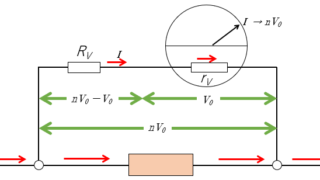 電磁気
電磁気 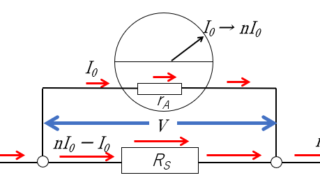 電磁気
電磁気 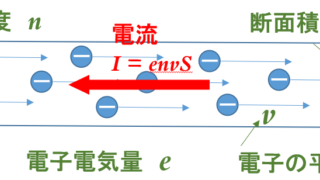 電磁気
電磁気 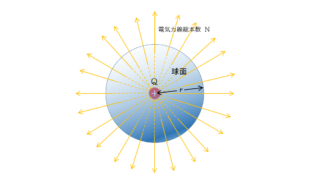 電磁気
電磁気