物理のエッセンス原子分野 37番
静止している Ra の原子核が崩壊して、Rn 原子核と α 粒子になった。
Ra の質量を $M_0$ 、Rn の質量を $M_1$ 、 α 粒子の質量を $m_1$ とする。
- 発生するエネルギー $Q$
- α 粒子の運動エネルギー
を求めましょう。
1 発生するエネルギー $Q$
質量欠損を求めて $E=\Delta mc^2$ で計算すればいいだけです。

この場合の質量欠損分は $\Delta m= M_0-(M_1+m_1)$ なので、
$Q=\Delta mc^2$
$~~=\left( M_0-M_1-m_1 \right ) c^2$
となります。
2 α 粒子の運動エネルギー
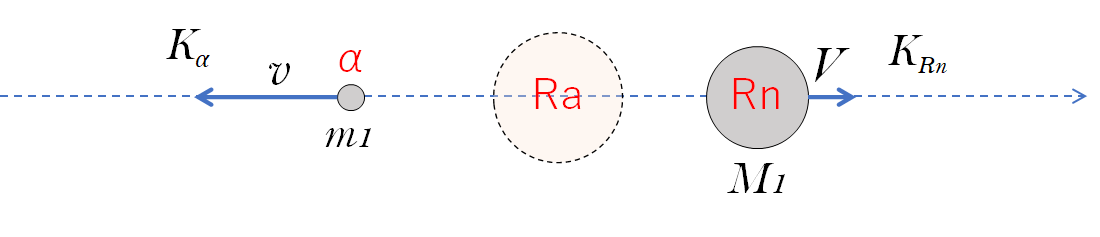
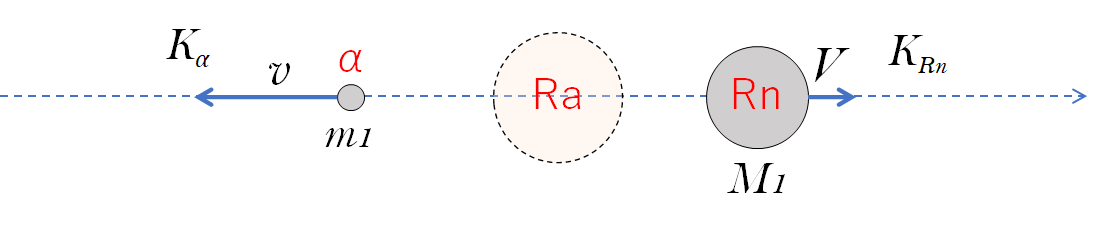
運動量保存則から考えて、発生した α 粒子と Rn は一直線上反対向きに飛んでいきます。

そのとき、α 粒子 ( 質量 $m_1$ ) の速さを $v$ 、Rn ( 質量 $M_1$ ) の速さを $V$ とします。
最初は静止していたので、図において右向きを正とすると、運動量保存則から
$0=M_1V-m_1v$
これより、
$v:V=M_1:m_1$ これより、$v=\dfrac{M_1}{m_1}V$
α 粒子の運動エネルギー $K_{\alpha}$ Rn の運動エネルギー $K_{Rn}$ とすると、
$K_{\alpha} : K_{Rn}=\dfrac{1}{2}m_1v^2 : \dfrac{1}{2}M_1V^2$
これに先ほどの $v=\dfrac{M_1}{m_1}V$ を入れて整理します。
$K_{\alpha} : K_{Rn} = m_1v^2 : M_1V^2$ $v=\dfrac{M_1}{m_1}V$
$~\quad\quad\quad \quad = m_1\left (\dfrac{M_1}{m_1}V \right)^2 : M_1V^2$
$~\quad\quad\quad \quad = m_1 \dfrac{M^2_1}{m^2_1}V ^2 : M_1V^2$
$~\quad\quad\quad \quad = \dfrac{M_1}{m_1}V ^2 : V^2$
以上より、
$K_{\alpha} : K_{Rn} = M_1: m_1$
また、 $K_{\alpha}+K_{Rn}=Q$ であるので、
$K_{\alpha} = \dfrac{M_1}{m_1+M_1}Q$
となります。このようなとき、運動エネルギーはそれぞれの質量の逆比になります。




















コメント