2023年共通テスト 物理基礎
中学レベル?の問題も結構ありました。
時間が短く、また1問の配点が相対的に高いので、焦ることなく粛々と解いていってほしいですね。
解いた感想は…例年よりちょっとだけ難化したのかも・・・です。
第1問
問1
箱Bが「受ける力」の$f_1$ と $f_2$ の大きさの関係について考えます。
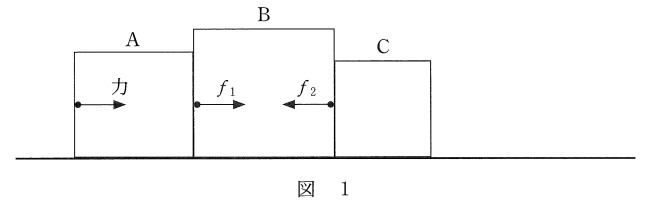
ここでBはニュートンの運動方程式を満たします。
図の右側方向に加速運動しているため、ニュートンの運動方程式は、
$ma=F$
です。この力 $F$ はBに働く力の合力だから、図の右向きを正として
$F=+f_1+(-f_2)=f_1-f_2$
となります。
ここで「加速運動を続けた」とあるので $a>0$ です。
したがって、
$ma=F=f_1-f_2>0$
より、 $f_1>f_2$ となります。
よって
1:答え ② 難易度 易

よくある勘違いとして $f_1=f_2$ とする人が見えますが、
その場合はBは等速運動し、加速しません。
問2
注意!2つのばねは、ばね定数が異なります。
そこでAのばねのばね定数を $k_\mathrm{A}$、Bのばねのばね定数を $k_\mathrm{B}$ とします。
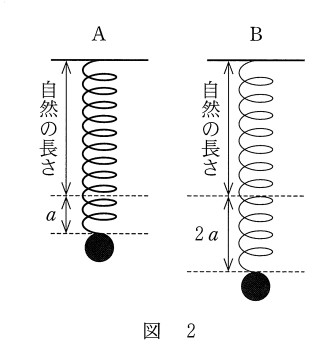
つり合いの関係から、
A:$mg=k_\mathrm{A}a$
B:$mg=k_\mathrm{B}(2a)$
より、$k_\mathrm{A}=2k_\mathrm{B}$ となります。
また、エネルギーを考え、
$\dfrac{\mathrm{ばねBの弾性力による位置エネルギー}}{\mathrm{ばねAの弾性力による位置エネルギー}}$
$\hspace{10pt}=\dfrac{\frac{1}{2}k_\mathrm{B}(2a)^2}{\frac{1}{2}k_\mathrm{A}a^2}$
$\hspace{10pt}=\dfrac{4k_\mathrm{B}}{k_\mathrm{A}}=\dfrac{4k_\mathrm{B}}{2k_\mathrm{B}}=2$
となります。よって
2:答え ⑤ 難易度 普通

早とちりして、ばね定数が同じとしてしまうと間違います。
問3
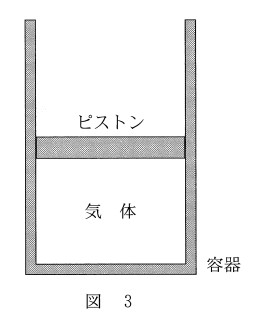
熱力学第1法則より、
$Q=\Delta U + W^{\prime}$
ここで、ピストン内に閉じ込められた気体の温度が上がるため、 $\Delta U > 0$ となります。
また、気体は外部に仕事をするため $W^{\prime}>0$ は明らかです。
したがって
$Q=\Delta U(>0) + W^{\prime}(>0)$
より、
$Q > W^{\prime}$
3:答え ③ $Q > W^{\prime}$ 増加 難易度 易
問4
ギターの基本振動が $110$ Hz であるため、きちんと調整すると4倍振動では、$4\times 110=440$ Hz を発することになります。
ここで「ギターの音の高さが低かった」ということですから、今、だいたいで調整したギターの4倍振動の音は $440$ Hz より少し小さい状態です。
「うなりが1秒当たり2回聞こえた」と、おんさの振動数 $440$ Hz より、
$2=440-f_{\mathrm{ギター}}$
よって、$f_{\mathrm{ギター}}=440-2=438$ Hz となります。……ウ

うなりは一般に $n=|f_1 – f_2|$ で示されます。
$f_1$、$f_2$は振動数
次に、ギター弦の調整ですが、波の式 $v=f\lambda$ より、 $f=\dfrac{v}{\lambda}$ です。
したがって、$\lambda$ が一定の時は、$v$ を大きくしていけば音 $f$ が高くなります。
問題文から、「弦の張力の大きさが大きいほど、弦を伝わる波の速さは大きくなる…」とありますから、低い音のギターの音を高く調整するためには、張力の大きさを少しずつ大きくしていけばよいことになります。
4:答え ④ 438 大きく 難易度 易

ギターを弾いたことがある人ならめっちゃ容易ですね。
第2問
問1
横の目盛間隔は一目盛りが 0.1 m ですから、左から4つ目の●の横の長さを図から読みます。
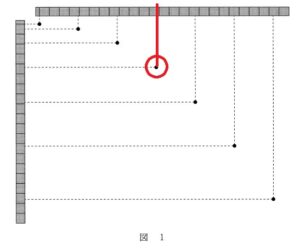
したがって、
5:答え ④ 難易度 易
問2
鉛直方向だけを考えます。
小球の鉛直下向きの速さ $v$ と時間 $t$ の関係は、$g$ を重力加速度として、
$v=gt$
ですから、縦軸を $v$ 、横軸が $t$ のグラフの場合、原点を通る直線になります。
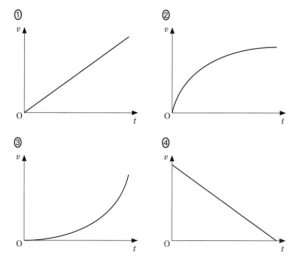
したがって
6:答え ① 難易度 易
問3
実験ア:水平投射
実験イ:水平投射の初速度の大きさを大きくした
実験ウ:水平投射の初速度の大きさを小さくした
アイウの実験を同じ高さから同時に行った場合、どの実験も鉛直方向には自由落下であるため、すべて床に同時に落ちます。
したがって、
7:答え ④ 難易度 易
床に到達した時の速さについて
力学的エネルギー保存法則によると、
位置エネルギー + 運動エネルギー =一定
です。
ここで出発時の位置エネルギーについては実験アイウすべてにおいて同じです。
しかし、出発時の運動エネルギーは、水平方向の速さの順番になるため、
実験イ > 実験ア > 実験ウ
となります。したがって、力学的エネルギーも
実験イ > 実験ア > 実験ウ
です。
この力学的エネルギーはそれぞれ保存されますから、床に到達時には実験イの力学的エネルギーが一番大きくなります。
また、床ではアイウすべてで位置エネルギーは同じです。
そのため、床での運動エネルギーは
実験イ > 実験ア > 実験ウ
となります。よって、
8:答え ② 難易度 易
問4

小球AおよびBが床に到達するまでの時間を $t$ とすると、
・小球Aについて、自由落下であることから
$h=\dfrac{1}{2}gt^2$
より、
$t=\sqrt{\dfrac{2h}{g}}\:\:\:\cdots(1)$
・小球Bについて、投げ上げの式から
$0=V_0t-\dfrac{1}{2}gt^2$
$(V_0-\dfrac{1}{2}gt)t=0$
$t=\dfrac{2V_0}{g}\:\:\:\cdots(2)$
よって、(1)(2)より、
$\sqrt{\dfrac{2h}{g}}=\dfrac{2V_0}{g}$
$V_0=\sqrt{\dfrac{gh}{2}}$
9:答え ⑥ 難易度 普通
問5
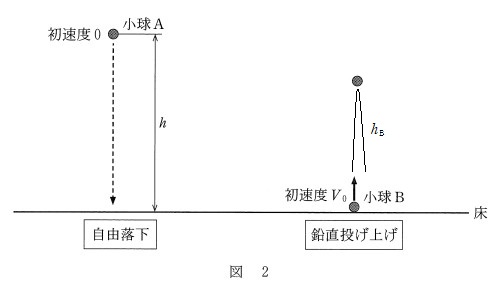
自由落下での $h$ と、鉛直投げ上げにおける最高点の高さ $h_{\mathrm{B}}$ を比較するのですが、わかりやすいようにグラフを描いてみました。
自由落下:鉛直下向きを正としています。
鉛直投げ上げ:こちらは鉛直上向きを正としています。
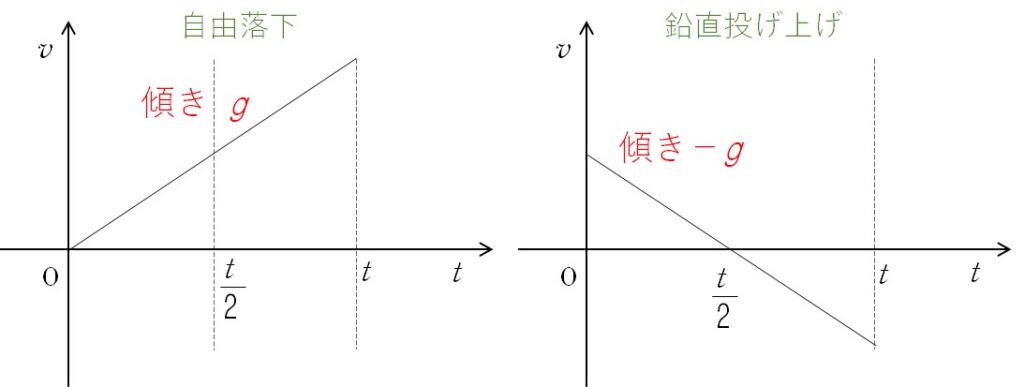

重要なのは、
どちらのグラフの傾きの大きさも、等しく $g$ であることです。
時間は等しく $t$ かかるわけですから、$h$ と $h_\mathrm{B}$ は下図のようになり、 $h>h_\mathrm{B}$ は明らかであることがわかります。


$v-t$ グラフで $t$ 軸とグラフの囲む面積が変位(距離)を表す…でした!
ちなみに、グラフから $h=4\times h_\mathrm{B}$ であることがわかります。
なぜって?
グラフから $h$ の三角形には $h_\mathrm{B}$ が4つ入りますね。
次に運動エネルギーですが、自由落下は高さ $h$ からの初速度 0 での落下です。
鉛直投げ上げの場合、打ち上げた小球が再び返ってきて床と衝突するときの運動エネルギーは、 床からの高さ $h_\mathrm{B}$ からの自由落下した時の床で持つ運動エネルギーと同じ値になります。

$h>h_\mathrm{B}$ でしたから、
$K_{h{\mathrm{A}}}> K_{h{\mathrm{B}}}$
も明らかです。よって、
10:答え ⑦ 難易度 普通
第3問
問1
選択肢から適するものを選びます。
風力発電は空気の「力学的エネルギー」を利用して‥‥太陽光発電を用いて「光」エネルギーを直接‥‥
したがって、
11:答え ① 難易度 易
12:答え ④ 難易度 易
問2
日本の一般家庭の1日の消費電力量はおよそ 18 kWh である。常に 10 m/s ~ 15 m/s の風が吹き続けていると仮定‣・・・・

グラフから、 10 m/s ~ 15 m/s の風が吹いているときの風力発電機の出力は、だいたい 20 kW であることがわかります。

ちょっと違うって?? 19くらい?
いいんです。 選択肢から選ぶんだから。
1日中、風が吹き続けていたとすると、風力発電機の出力した総電力量は、
$20 \mathrm{kW} \times 24 \mathrm{h(時間)}$
となります。したがって、
$20 \:\mathrm{kW} \times 24 \:\mathrm{h(時間)} \div 18 \simeq 24$
よって答えは、
13:答え ⑥ 難易度 易
問3
送電線の抵抗 $r$ によって生じる電力損失は次の式で計算できます。
$P=I^2r$
これより $I$ を$10^{-3}$ 倍にすれば、2乗で効いてくるため電力損失は $10^{-6}$ 倍になります。
14:答え ② 難易度 易
発電所から出力された電圧と電流の関係は
$P=IV$
の関係があるため、電流を $I$ を$10^{-3}$ 倍にしたときには、電圧 $V$ を$10^{3}$ 倍にすればよいことになります。
15:答え ③ 難易度 易

どうもしっくりこない人へ
これは当ブログで詳しく解説してます。こちらをご覧ください。

問4
変圧器の物理です。電磁誘導ですね。

この場合、次の関係式があります。
$N_1:N_2=V_1:V_2$
より、
$V_2=\dfrac{N_2}{N_1}V_1$
16:答え ⑥ 難易度 易







































コメント