概観
文章量が多く、読解力が要求される。
思いのほか時間がかかったのではないでしょうか?公式暗記組は苦戦したと思います。
物理得意組も、時間配分を間違えれば危うい展開もあったかも。
私自身が解いてみた感想では、点数的にはともかく内容的には昨年より難化?
(昨年が簡単すぎた?…でも平均点は今年の方が昨年より高いみたいです??)
2023年 共通テスト 物理 解説
(昨年が簡単すぎた?…でも平均点は今年の方が昨年より高いみたいです??)
問題はこちらから
第1問
問1
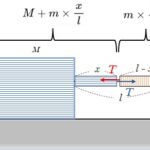
モーメントの問題です。
問題の状況を簡単に図示してみます(下図)。
体重計で測ると、60 kg と言っているので、重量が60 kgf としています。

図より、 図の $W$ の作用点周りのモーメントとして $F_a\times 2 = F_b \times 1$ また、 $F_a+F_b=60$ であるから、
$F_a=20$ kgf $F_b=40$ kgf
を得ます。 答え ③ 易
というか暗算で、$F_a:F_b=1:2$ だな…としてOKです。
問2
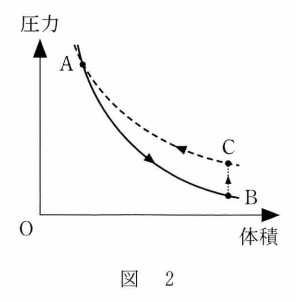
問題から、A→B:断熱膨張 B→C:定積変化 C→A:等温変化
- 2
気体の内部エネルギーの変化分 $\Delta U$ は絶対温度に比例し、
$\Delta U=k\Delta T$ $k$:比例定数 $T$:絶対温度
です。

ここではどのような気体か不明のため、
比例定数 $k$ として
絶対温度に比例するとしました。
内部エネルギーは温度変化に伴って変化はしますが、サイクルを1周すると温度が元に戻りますから $\Delta T=0$ 、したがって $\Delta U=0$ です。
答え ③ 難易度 易
- 3
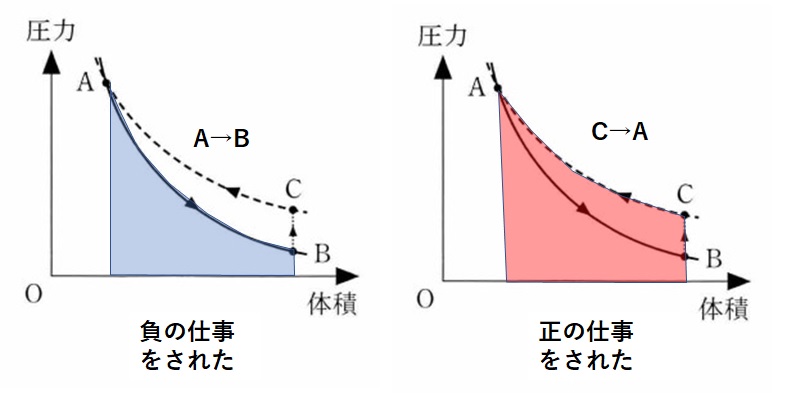
このサイクルを1周する間にされた仕事の総和は、図の線で囲まれた内部の面積で示されますが、「気体のされた仕事」はA→Bで負、B→Cは仕事0、C→Aは正になります(図)。

ここで問題は、
「気体のした仕事」ではなく、「気体のされた仕事」
であることに注意してください。
これで間違えた人も多いかもしれませんね。
それぞれの仕事を示す面積を比較すると、「負の仕事の大きさ」<「正の仕事の大きさ」ですから、全体としての「気体のされた仕事」は「正」になります。
よって、1サイクルでは「気体のされた仕事」 $W>0$ です。
ア:正
1サイクル(A→B→C→A)で考えるとき、 $Q=\Delta U\: -\: W$ ($W$ は気体のされた仕事)において、温度 $T$ は元に戻るため $\Delta U =0 $ です。
したがって、気体が吸収した熱量 $Q$ は熱力学第1法則(ただし $W$ はされた仕事)、 $Q=0-W$ より、$Q<0$ … イ:負
答え:③ 難易度 普通
問3
力学的エネルギーとは、「位置エネルギー + 運動エネルギー」です。
摩擦などの非保存力がはたらかないときに保存されます。
運動量保存則は、系に対して外力が働かないときに成立します。
力学的エネルギーについて
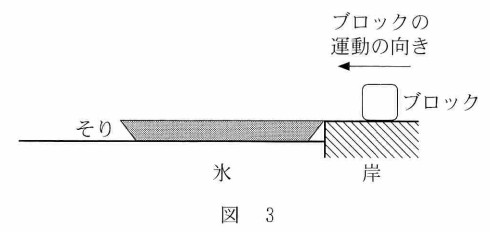
この問題では、
・「そりが岸に固定されていて動けない場合」
・「そりが固定されておらず、氷の上を左に動くことができる場合」
のいずれにおいても、そりとブロックの間の摩擦は無視できないため、力学的エネルギーは保存されません。
運動量保存について
- 「そりが岸に固定されていて動けない場合」
そりは氷の上を滑らないため外力を受けており、水平方向の運動量はそりとブロックの間では保存されません。 - 「そりが固定されておらず、氷の上を左に動くことができる場合」
そりとブロックの間には摩擦がありますが、内力であるため、そりとブロックを系とした場合、水平方向の運動量は保存されます。(そりと氷の間には摩擦がない)
以上より
4 答え ④ 難易度 易
5 答え ② 難易度 易
問4
フレミング左手測から、正の荷電粒子が回る方向は「反時計回り」です。また、負の荷電粒子の回る方向は「時計回り」になります。これで答えは ② か ④ に絞られます。
また、回転半径を $r$ 、荷電粒子の質量を $m$ 、荷電粒子の速さを $v$ 、荷電粒子の電荷 $q$ 、磁束密度 $B$ とした場合、
向心力=ローレンツ力
であるから、
$m\dfrac{v^2}{r}=qvB$
よって、荷電粒子が等速円運動する際の回転半径 $r$ は、
$r=\dfrac{mv}{qB}$
となります。ここで $q$、$B$、$v$ は共通なので、粒子の質量 $m$ の大きい方が回転半径 $r$ は大きくなります。「正の荷電粒子の質量」>「負の荷電粒子の質量」であるから
答え ④ 難易度 普通
問5
光電効果の問題です。
光電効果の式
$h\nu=K_0+W$
です。グラフから、 $\nu_0$ のとき、 $K_0=0$ ですから、
$h\nu_0=W$

したがって、
$h=\dfrac{W}{\nu_0}$
答え ⑤ 難易度 易
第2問
問1
- 空気の抵抗力 $R=kv$ $k$:比例定数
- 運動方程式、$ma=mg-R$
とするなら、ア:逆 イ:増加 ウ:減少 となります。
答え ⑥ 難易度 易

$R=kv^2$ $k$:比例定数
だったとしても答えは変わりません。
問2
表1を見ると、$n=3$ のとき、20 ㎝ を通過するのに要する時間は落下後少しすると、0.13 s で安定していることがわかります。
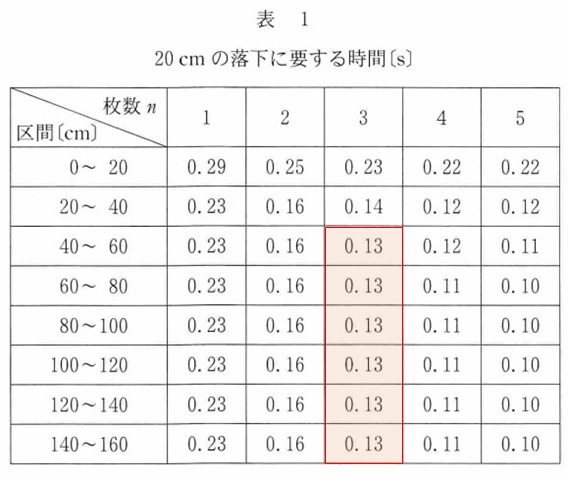
したがって、落下距離が 40 cm 以降は終端速度に達して等速運動しているとみなせますから、
$v=\dfrac{\Delta x}{\Delta t}=\dfrac{20\times 10^{-2}}{0.13} \fallingdotseq 1.53\times 10^{0}$
9・10・11 の答え $1.5\times 10^{0}$ 難易度 易
問3
予想の $v_f=\dfrac{mg}{k}$ は アルミホイルの1枚の質量を $m_1$ とすると、
$v_f=n \times \dfrac{m_1g}{k}$
と示すことができます。ここで、 $\dfrac{m_1g}{k}=K$ とおくと、
$v_f=Kn$ $K$:定数
ですから、$v_f-n$ グラフにおいては、原点を通る直線となります($y=Kx$ グラフと同様)。
しかし、実験によるグラフは下図のようになっているため、無理に直線を引くと、その直線は原点を外れてしまいます。
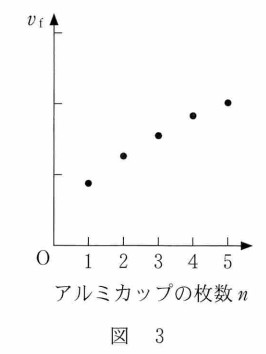
したがって、答え ② 難易度 易
問4
ここでは、空気の抵抗力を
$R=k^{\prime}v^2$
とし、
$v_f=\sqrt{\dfrac{mg}{k^{\prime}}}$
としています。問3と同じように、アルミホイルの1枚の質量を $m_1$ とすると、
$v_f=\sqrt{\dfrac{mg}{k^{\prime}}}$
$\:\:\:\:\:\:\:\:\:=\sqrt{n \times \dfrac{m_1g}{k^{\prime}}}$
ここで、 $\sqrt{\dfrac{m_1g}{k^{\prime}}}=K^{\prime}$ としてやると、
$v_f=K^{\prime}\sqrt{n}$
となり、$v_f-\sqrt{n}$ のグラフでは原点を通る直線となります。
あるいは、 両辺を2乗して、
$v^2_f=(K^{\prime})^2 n$
ここで、 $(K^{\prime})^2=K^{\prime\prime}$ として
$v^2_f=K^{\prime\prime}n$
としてやると、$v^2_f-n$ のグラフで原点を通る直線となります。
したがって、答え ④ と ⑧ 難易度 普通
問5
- エ
(a):加速度は $v-t$ グラフから一定値ではないことがわかります。×
(b):終端速度に到達すると加速度は 0 になります。×
(c):加速度は $a=\frac{\Delta v}{\Delta t}$ で示されます。〇 - オ
運動方程式 $ma=mg-R$ より、 $R=m(g-a)$ と示されます。(c)
したがって、答え ⑨ 難易度 易
第3問
よく見る典型的な問題ですが、多少ひねりがきいています。
問1
向心力は $m\dfrac{v^2}{r}$ で示されます。
また、この問題では、向心力は運動方向に対して常に垂直のため、音源に対して仕事をしません。よって、0です。
答え ⑤ 難易度 易
問2
音源と観測者が相対的に近づくときは音(振動数)は高く聞こえ、離れるときは音(振動数)は低く聞こえます。
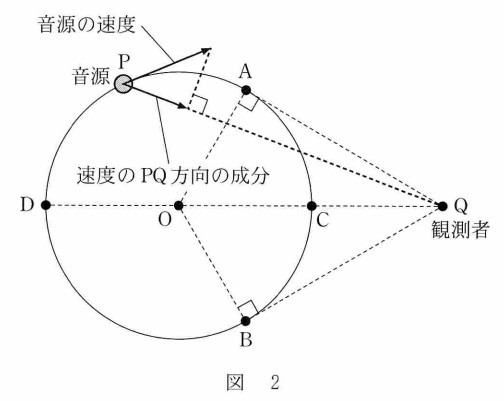
図のように円運動している状態では、C点とD点においてのみQの方向に音源の速度成分が0になります。
したがって、 答え ⑥ 難易度 易
問3
A点:音源のAQ方向の速さは $v$ で接近しています。観測者へ向かうの音源の速さが最大となるため、観測者は最も高い音を聞きます。
B点:音源のBQ方向の速さは $v$ で遠ざかっています。観測者から遠ざかる音源の速さが最大となるため、観測者は最も低い音を聞きます。

ドップラー効果の式
$f=\dfrac{V-v_o}{V-v_s}f_0$
から、
$f_A=\dfrac{V}{V-v}f_0\:\:\cdots(1)$
です。よって答えは、⑤か⑥です。
同様に
$f_B=\dfrac{V}{V-(-v)}f_0$
$\:\:\:\:\:\:\:\:=\dfrac{V}{V+v}f_0\:\:\cdots(2)$
$\frac{(1)}{(2)}$ とすると、
$\dfrac{(1)}{(2)}=\dfrac{f_A}{f_B}=\dfrac{\dfrac{V}{V-v}f_0}{\dfrac{V}{V+v}f_0}$
$\dfrac{f_A}{f_B}=\dfrac{V+v}{V-v}$
これより変形して次式を得ます。
$v=\dfrac{f_A-f_B}{f_A+f_B}V$
よって、答え ⑥ 難易度 普通
問4
今度は、音源と観測者を入れ替えます。
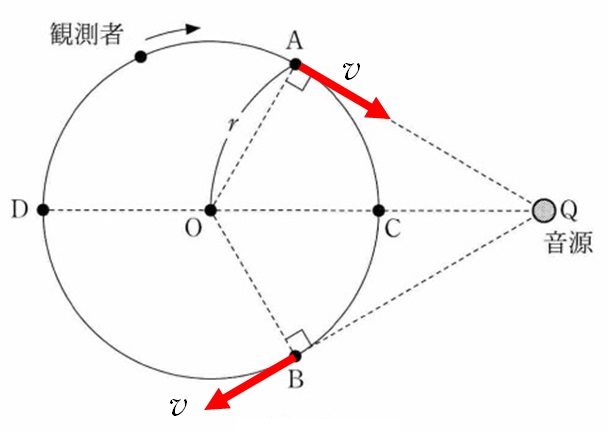
その場合の、等速円運動をする観測者が測定する音の振動数について考えます。
A点:観測者のAQ方向の速さは $v$ で接近しています。音源へ向かうの観測者の速さが最大となるため、観測者は最も高い音を聞きます。
B点:観測者のBQ方向の速さは $v$ で遠ざかっています。音源から遠ざかる観測者の速さが最大となるため、観測者は最も低い音を聞きます。
- ① 〇
- ② B点は遠ざかり、A点は近づくため逆です。
- ③ 点Cと点Dではドップラー効果は生じません。
- ④ 点Cと点Dではドップラー効果は生じません。
- ⑤ 音源と観測者が相対的に運動している場合にドップラー効果が観測されます。
答え ① 難易度 易
問5
正しいものの組み合わせを2つ選ぶことに注意しましょう。


図1は音源が等速円運動し、図3では観測者が等速円運動しています。
- (a) 音源の速さによって、音源から伝わる音の速さは変化しません。×
- (b) 原点Oに観測者がいると仮定してみましょう。
Oから見て等速円運動する音源の速度は常にOと音源を結ぶ動径に対して垂直です。
したがって、Oが聞く音の波長は、音源の等速円運動によって変化しません。〇 - (c) 音源は静止しているので,音源から見た音の速さは変化しません。〇
- (d) 音源が静止しているため、すべての場所で波長は同じです。×
答え ④ 難易度 普通
第4問
コンデンサーの電場・電位などの出題。
問1
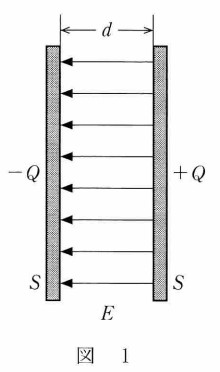
ア: $E=\dfrac{V}{d}$
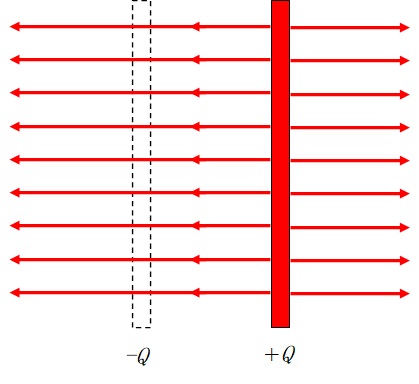
問題に書いてあるように二つの極板に挟まれたところには $4\pi k_0 Q$ 本の電気力線があります。

ここで、$2\times 4\pi k_0 Q$ 本では? と思った人はいませんか?
次の図のように考えてみます。
まず、次の図に示された赤の電気力線の総本数は $4\pi k_0 Q$ 本ですね。
したがって、図の左に向かって伸びている電気力線の数は $2\pi k_0 Q$ 本です。
同様に、次の図に示した青の電気力線も $4\pi k_0 Q$ 本です。
したがって、図の左から右に向かって伸びている電気力線の数は $2\pi k_0 Q$ 本です。

これらの電気力線(赤と青の→)はコンデンサーの外側では打ち消しあっています(下図)。
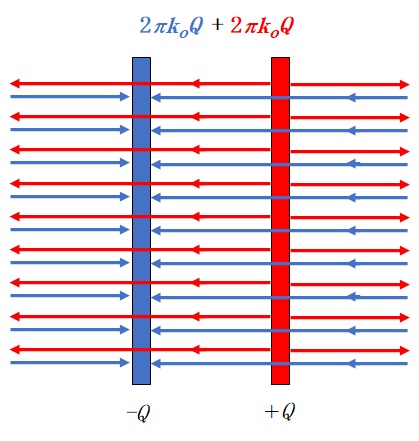
コンデンサーの極板の内部では $2\pi k_0 Q$ ずつあるため、コンデンサー内部の電気力線総本数は、
$2\pi k_0 Q +2\pi k_0 Q$ 本
となり、よってコンデンサー内部の電気力線本数は $4\pi k_0 Q$ 本となります。
電場の大きさは、単位面積当たりを垂直に貫く電気力線本数で示されます(というか、これが電気力線の定義)。よって、極版面積が $S$ であることから、
$E=\dfrac{V}{d}=\dfrac{4\pi k_0 Q}{S}$
これを変形して、
$Q=\dfrac{S}{4\pi k_0 d}\cdot V$
これと、 $Q=CV$ とを比較して
$C=\dfrac{S}{4\pi k_0 d}$
を得ます。
答え ⑧ 難易度 普通
問2

スイッチを開く直前の電圧計は 5.0 V を示していました。
よって充電されたコンデンサーの極版間電圧は 5.0 V です。
問題では下図より、この実験で用いた抵抗の大きさを求めます。
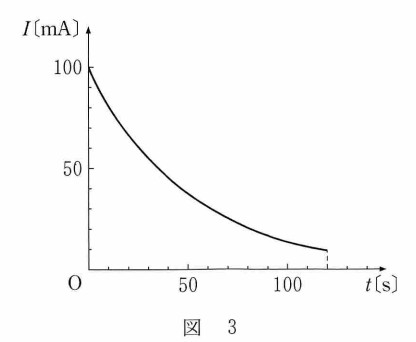
ここでは、時間 $t=0$ の時を考えます。図より、$I=100$ mA です。
コンデンサの極版間の電圧は 5.0 V でした。
抵抗と電源とは並列接続ですから、スイッチを開く前に抵抗に 5.0 V かかっており、電流は 100 mA です。(あるいは、$t=0$ ではスイッチを開いた直後と考えて、コンデンサはその瞬間だけ、 5.0 V の電源とみなす、としてもかまいません。)
したがって、オームの法則より
$R=\dfrac{V}{I}=\dfrac{5.0}{100\times 10^{-3}}=50$ Ω
が得られます。
答え ⑦ 難易度 普通
問3
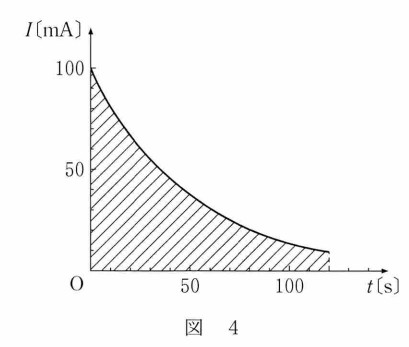
- 23
横軸の 1 ㎝ を 10 s 、縦軸の 1 ㎝ を 10 mA としていることから、1 ㎝$^2$ の面積の示す電気量 $Q$ は
$Q=It=10 \:\mathrm{mA} \times 10 \:\mathrm{s}=100 \:\mathrm{mC} =0.1 \:\mathrm{C}$
となります。答え ③ 難易度 普通

ここでは $Q=It$ を使いました。
- 24
グラフの面積を数えると 45 cm$^2$ でしたから、コンデンサーに蓄えられていた電気量 $Q$ は、
$Q=0.1\times 45 =4.5$ C
となります。コンデンサーの電圧は 5.0 V でしたから、 $Q=CV$ より、
$C=\dfrac{Q}{V}=\dfrac{4.5}{5.0}=0.90$ F
したがって、答え ⑧ 難易度 普通
問4

半減期 35 s のモデルとして考えてみます。$t$ 秒後について、
$\dfrac{N}{N_0}=\left ( \dfrac{1}{2}\right)^{\dfrac{t}{35}}$
が成り立ちます。$\frac{1}{1000}$ になるわけですから、
$\dfrac{1}{1000}=\left ( \dfrac{1}{2}\right)^{\dfrac{t}{35}}$
より、
$t=\dfrac{3\times 35}{\log_{10}2} \fallingdotseq 350$
( ただし、 $\log_{10}2 \fallingdotseq 0.30 $ )
対数の値がわからない場合、要は選択肢から選べばいいんですから、
$\left ( \dfrac{1}{2} \right ) ^{10}=\dfrac{1}{1024}\fallingdotseq \dfrac{1}{1000}$ となることから、
$35 \times 10 =350 $ としましょう。
答え ④ 難易度 普通
問5
Aさんの言葉の中にヒントがあります。
「コンデンサーに蓄えられていた電荷が抵抗を流れるときの電流はコンデンサーの電圧に比例します。」
グラフから $t=35$ s の時の電流値を読み取ります。$I_0=100$ mA ですから、$I=50$ mA 。
抵抗は 5.0 Ω ですから、そのときの電圧 $V$ はオームの法則から$V=RI=5.0 \times 50 \times 10^{-3}=2.5$ V $\cdots\:(1)$

「コンデンサーに残っている電気量もコンデンサーの電圧に比例します。」
$t=35$ s の時にコンデンサーに残っている電気量 $Q^{\prime}$ は、$Q=CV$ と、上記から $V=2.5$ V であることから、
$Q^{\prime}=CV=C\times 2.5$
コンデンサーが最初に持っていた電気量 $Q_0$ は、
$Q_0=CV=C\times 5.0 \: \cdots\:(2)$
したがって、$t=35$ までにコンデンサーから放出された電気量 $Q_1$は、
$Q_1=Q_0 – Q^{\prime}=C\times 5.0-C\times 2.5=C\times 2.5 \: \cdots\:(3)$
$(2)$、$(3)$ 式より、 $Q_0=2\times Q_1$ となります。
ウ 答え $2Q_1$

問題文には明記されておりませんが、
ここでは、抵抗 $R$ は、非線形抵抗ではなく、
オームの法則に従うとしています。
また、最初の方法では、面積を小さく見積もっているため、正しい電気量よりも小さい値になっています。
つまり、 $Q=CV$ の式で、 $Q$ を小さく見積もってしまったため、
$C=\dfrac{Q}{V}$
の式より最初の方法で見積もられた $C$ は「小さかった」ということになります。
エ 答え 小さかった
答え ⑤ 難易度 やや難






































コメント