2022年 共通テスト 物理基礎 解説

2022年度の物理基礎は例年よりかなり難化したのではないでしょうか。
（まあ、例年が簡単すぎたかも）

今年の専門物理はけっこう簡単な問題が多いように思いましたが・・・。
（気のせい？）

2022年 共通テスト 物理基礎 解説

第1問

問1

A→Bの相対速度の大きさと、通過時間を問われています。

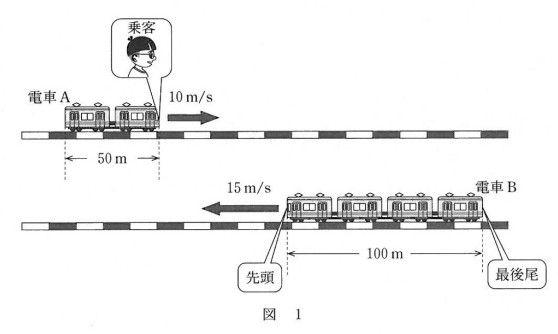
• ア　　相対速度ですが、Aに対するBの相対速度 $v_{AB}$ は

$v_{AB}=v_B-v_A$

で示されました。

よって、この場合図の右向きを正とすると、

$v_{AB}=v_B-v_A=-15-10=-25$ m/s

で、大きさは 25 m/s です。

• イ　　

AからBを見ると、大きさ 25 m/s で、向かってくるように見えます。

相対速度は自分を静止しているとして考えられますから、Aが静止してBが 25 m/s で接近してくるとしてOKです。

そうすると、長さ100 m の列車が 25 m/s の速さで静止しているAの横をすり抜けていくとして計算すればよいことになります。

したがって、

$t=\dfrac{x}{v}=\dfrac{100}{25}=4.0$ 秒

ア　25　　イ　4.0　だから　

答えは⑦　　難易度　易

 

問2

はじめは静止。続いて上向きに力を加えて、最後に最初と同じだけの力をかけます。

そのときの運動の様子を問われています。

最初は静止しているため、小球にはたらく力は重力 $mg$ と同じ大きさです。

 

次に上向きに力を増したので、運動の法則 $ma=F$ にしたがって加速運動します。

その後、力を $mg$ にもどしたので、先ほど加速した最後の速度を保って等速直線運動を続けます。

したがって、

• 区間1・・・静止している 　　a
• 区間2・・・一定の加速度で速さが増加しながら鉛直方向に上昇している　　c
• 区間3・・・一定の速さで鉛直方向に上昇している　　b

よって　答えは　④　　難易度　易

問3

図のように小球を打ち上げるときのy座標と運動エネルギー・位置エネルギーの関係を選ぶ問題です。

位置エネルギーの基準は $y=0$ です。グラフは以下から選びます。

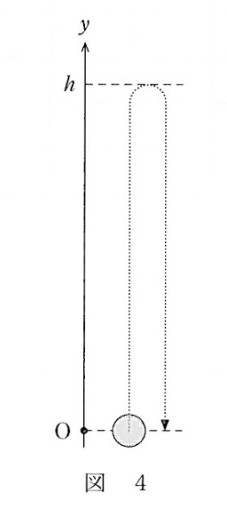
力学的エネルギー保存則から式をたててみましょう。
小球の質量 $m$ 、初速度の大きさ $ⅴ_0$、 途中の高さ $y$ 、そのときの速さ $v$ 、重力加速殿大きさ $g$ とします。 

$\dfrac{1}{2}mv_0^2=\dfrac{1}{2}mv^2+mgy=mgh=C$ (一定)

ここで、グラフの縦軸は（運動・位置）エネルギー　横軸は　$y$　であることに注意します。

 

運動エネルギーを考えるので　$\dfrac{1}{2}mv^2=K$　としてみます。

そうすると、

$K+mgy=C$

という式になりますから、 式を変形して　$K=-mgy+C$　です。

この式を　$K\rightarrow y $    $y\rightarrow x$　 $mg \rightarrow a$ 　として書き換えてみると

$K=-mgy+C$　　⇒　　$y=-ax+C$

これはなじみのある式ですね。運動エネルギーを示すもので、この式にあうものは (c) ですね。　

横軸が時間軸ではなく $y$ ですから上昇中も下降中もグラフの形は同じです。
よって上昇・下降のどちらも (c) となります。

また、力学的エネルギー（運動エネルギー＋位置エネルギー）は保存され、位置エネルギー  $U=mgy$ も(c)のようになります。

答えは　⑨　　普通

 

問4

図の波の速さと状態を答えます。

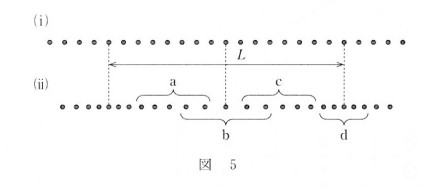
• ウ

図から波の速さを計算します。
これは縦波ですから、横波に直したものを次に示します。
注意：見やすいように赤の横波の振幅を拡大しています。

これよりこの波の波長は $L$ だとわかります。

また、再びこの形になるまで $T$ だけ時間がかかったのであるから、この波動の周期は $T$ だとわかります。

したがって、 $v=\dfrac{\lambda}{T}$　より、

$v=\dfrac{\lambda}{T}=\dfrac{L}{T}$

 

• エ　　

図の (ii) のa,b,c,d のうちで媒質の変位が全て左向きのものを探します。
再び、先ほどの図を示します。

下図に示したように、横波表示にした場合に下向き変位のものは縦波では左向きです。

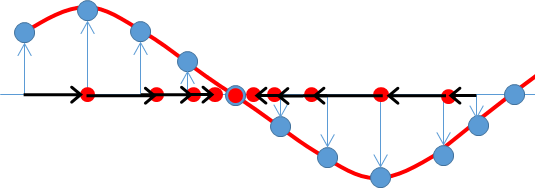
ということは、媒質の変位が、全て左向きのものは a の部分だとわかりますね。

 

よって　答えは　⑤　　難易度　普通

 

第2問

この問題は今回の問題の中では、難しい部類に入ると思います。
というか、勘違いしやすいかも。

問1

図のようにして通電したところ、電熱線Aを入れた水のほうの温度が高かった。
というものです。

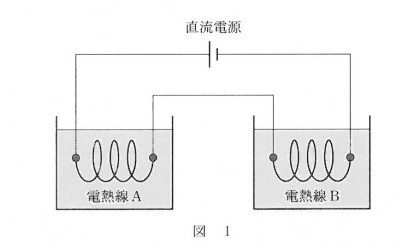
ここで、電熱線Aによるほうの温度が高い　⇒　電熱線Aの抵抗が大きいか小さいか？

を考えてみます。

答えは「電熱線Aのほうの抵抗が大きい」です。間違える人が多いかも。

 

これは　$P=IV=I^2R=\dfrac{V^2}{R}$　から考えましょう。

この回路は直列ですので、電熱線Aと電熱線Bを流れる電流は同じです。
したがって、先ほどの式から　$P=I^2R$　で比較するとラクできそうですね。

となると $P$ が大きくなるのは $R$ の大きいほうだとわかります。
したがって、より発熱した電熱線Aの抵抗が大きいのです。

また、オームの法則　$V=RI$　から、電流 $I$ が同じなので $R$ が大きいほうの電熱線の $V$ が大きくなります。 

したがって、答えを選択肢から探すと　ウ　となります。

答え　③　難易度　普通

 

問2

次に、並列にしたものを考えます。
下図では電熱線Cを入れた水のほうが温度が高くなりました。

ここで、電熱線Cによるほうの温度が高い　⇒　電熱線Cの抵抗が大きいか小さいか？

かを考えましょう。

答えは「電熱線Cのほうの抵抗が小さい」です。これも、間違える人が多いのでは？

 

$P=IV=I^2R=\dfrac{V^2}{R}$　から考えましょう。

この回路は並列ですので、電熱線Cと電熱線Dにかかる電流は異なりますが、電圧は同じになります。

よって、先ほどの $P$ の式から　$P=\dfrac{V^2}{R}$　で考えます。

そうするとより $P$ が大きくなるのは $R$ の小さいほうです。
したがって、電熱線Cのほうが抵抗が小さいのです。

次に、それぞれを流れる電流の大きさを考えましょう。
オームの法則　$I=\dfrac{V}{R}$　より、$V$ が同じだから $R$ の小さいほうに多くの電流が流れます。したがって、電熱線Cには電熱線Dよりも多くの電流が流れます。

ということで　選択肢から合うものを探すと　ア　イ　です。

答え　④　　難易度　普通

 

問3

ドライヤーの問題です。

ドライヤー全体で消費されている電力 $P$ 、電熱線で消費されている電力 $P_h$ 、モーターで消費されている電力 $P_m$ についての関係式を考えます。

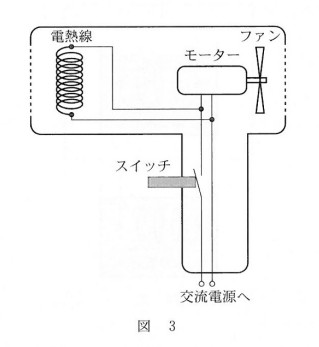
$P$ は単位時間当たりのエネルギー量を示しています。

したがって、エネルギー保存則から　$P=P_h+P_m$　が成り立ちます。

答え　④　　難易度　易

 

問4

電熱線の抵抗値が 10 Ω であるときの2分間の、電熱線で消費される電力を求めます。
交流電源は 100 V としています。(ジュール熱 Q　電力 P　時間 t) 

$Q=Pt$　　$P=IV=I^2R=\dfrac{V^2}{R}$　　

から考えます。2分間は　$2\times 60 $ 秒ですから、　

$Q=Pt=\dfrac{V^2}{R}t$

$~~~=\dfrac{100^2}{10}(2\times 60)$

$~~~=1.2\times 10^5$ J

 

答えは　8　①　　難易度　易

　　　　9　②　　難易度　易

 

第3問

アルキメデスのお話から着想を得ているのでしょう。
しかし、中身は浮力のお話だけではなくいろいろ出てきます。

問１

王女と細工師はまず、スプーンの比熱を測定します。

比熱(比熱容量）とは、物質の温度 1 g を 1K 高めるために必要な熱量です。

スプーンAとスプーンBは同じ質量です。温度をともに 60.0 ℃ にして、20.0℃の水200.0 g にいれて熱平衡にします。

結果

• スプーンAを水に入れた場合の水の温度：20.6℃
• スプーンBを水に入れた場合の水の温度：20.7℃

スプーンBを入れた水の温度のほうが高くなりましたから、スプーンBの持っていた熱量のほうがスプーンAの持っていた熱量よりも大きかったことを示しています。

スプーンAとスプーンBは同じ質量ですから、もしスプーンを同じ温度から60.0℃まで暖めるとした場合、より多くの熱が必要だったのはスプーンBです。したがって、（１０）スプーンBのほうが比熱が「①大きい」ことがわかります。

ただし、2つの温度差は 0.1℃という小さいものだったので、（１１）水の量を「②半分」にしていれば、あるいは（１２）水に入れる前のスプーンと水の温度差を「①大きく」していれば結果の違いはもう少し大きく出たと考えられます。

スプーンの持つ熱量を水に与えるわけですから、もらう側の水の量を半分にすれば、水の温度上昇は大きくなります。
また、水の温度差を大きくしておくことで移動する熱量が大きくなります。

 

答え　10　①　　難易度　易

　　　11　②　　難易度　易

　　　12　①　　難易度　易

 

問２

密度を比較します。アルキメデスの実験ですね。

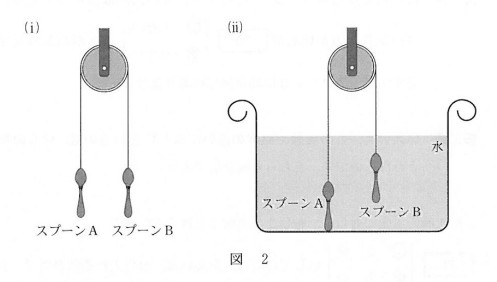
浮力は物体の体積だけで決まります。
式で示せば　浮力 $F$ 、　まわりの水の密度 $\rho$ 、　重力加速度 $g$ 、　体積 $V$ とすると、

$F=\rho gV$　

スプーンAとスプーンBの質量は同じです（図(i)）。
したがって（１３）スプーンBとスプーンAにはたらく重力の大きさは「③同じ」

 

図(ii)からスプーンAが下がりましたから、（１４）スプーンBの浮力の大きさは、スプーンAにはたらく浮力の大きさ「①よりも大きい」

 

先ほど述べたように、浮力はその物体の体積だけで決まりますから、

（１５）スプーン Bの体積はスプーンAの体積よりも「①大きい」ことがわかります。

 

答え　13　　③　　難易度　易

　　　14　　①　　難易度　易

　　　15　　①　　難易度　易

 

問３

次は電気抵抗ですね。

スプーンから長さ 1.0 m 、断面積 $2.0\times 10^{-8}\:\mathrm{[m^2]}$ に精密に加工できるなんて・・・・時代はいつなんだろう？？？　　スプーンこわしちゃってよかったのでしょうか？？

では考えていきましょう。電流ー電圧 グラフです。

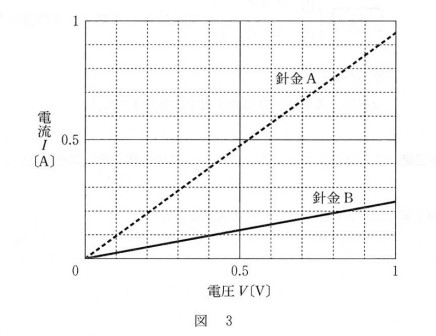
• 16

図のグラフは直線ですから、電気抵抗は、単純にオームの法則を適用すればOKです。

グラフから $V$ と $I$ の大体の数値を読みます（読みやすいところどこでも可）。
ここでは 0.4 V   0.1 A　ぐらいを目安にします（選択肢から選ぶので大体でいいでしょう）

したがって針金B（スプーンB）の電気抵抗 $R$ は

$R=\dfrac{V}{I}=\dfrac{0.4}{0.1}=4$ Ω

選択肢で近いのは　③ の 4.1 Ω

16 　答え　③　　難易度　易

 

• 17

抵抗率 $\rho$ 、針金の断面積 $S$ 、針金の長さ $l$ とすると

$R=\rho \dfrac{l}{S}$

より

$\rho=R\dfrac{S}{l}$

だから　17の答え　④　　難易度　易　

 

細工師は逃げ出した

アルキメデスのときは、不正がばれた細工師は王様に首をはねられたのように聞いたことがあります・・・。