概観
一見難しそうに感じても問題文中にヒントがちりばめられており,よく理解できていないものでもそのヒント通りに考えていけば解答できる問題が多くあります。また,「公式」を暗記していればソッコーで解答できる問題も。
その一方で新しい視点からの問題もあって,玉石混交の感がありました。
総合して難易度は例年並みでしょうか?
2025年 共通テスト 物理 解説
問題はこちらから
https://www.toshin.com/kyotsutest/data/3073/butsuri.pdf
第1問
問1
山頂(圧力 $P_0$ 体積 $V$ 絶対温度 $T_0$)とふもと(圧力 $P_1$ 体積 $V-\Delta V$ 絶対温度 $T_1$)から,山頂での大気圧 $P_0$ を求めます。
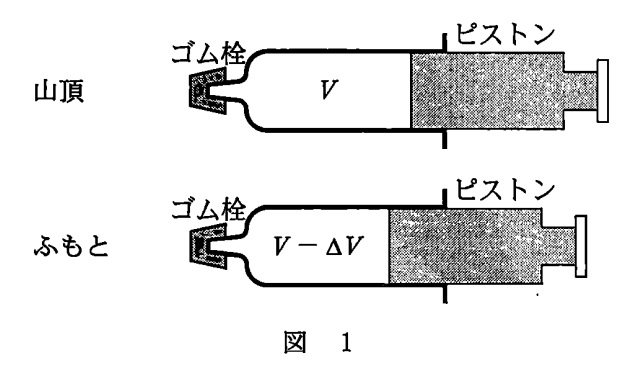
注射器のピストンは滑らかに動く ⇒ 注射器の内部の圧力=外気圧 であることに注意します。
したがって,山頂での注射器の内部圧力は $P_0$で温度は $T_0$,ふもとでは $P_1$で $T_1$ です。
これは普通にボイルシャルルを適用すればよいので,
$ \dfrac{P_0 V}{T_0}=\dfrac{P_1 (V – \Delta V)}{T_1}$
より,
$ P_0 = \dfrac{P_1 (V – \Delta V)T_0}{VT_1}$
答えは 4 難易度 易

これは落とせない。
問2
重力と万有引力の関係から,地球質量を求めます。
問題文「$mg$ となる。この力は。地球の全質量 $M$ が地球の重心に集まった時の万有引力に等しい」より,
$ mg = G\dfrac{mM}{R^2}$
これより,
$ M = \dfrac{gR^2}{G}= \dfrac{9.8 \times (6.4 \times 10^6)^2}{6.7 \times 10^{-11}}$
ですが,選択肢から答えを選ぶだけなので,計算は概算でよくて,
$ \dfrac{10 \times (6 \times 10^6)^2}{6 \times 10^{-11}}= 6.0 \times 10^{24}$ Kg
とすればよいでしょう。地球質量が $ 6.0 \times 10^{24}$ kg だと知っていればそれでもOKです。
したがって
答えは 9 難易度 易

地球の質量(kg)ってアボガドロ数$ 6.0 \times 10^{23}$の約10倍,とすれば覚えやすいですね。
ちなみに,太陽の質量は,約 $2.0 \times 10^{30} $ kg です。
問3
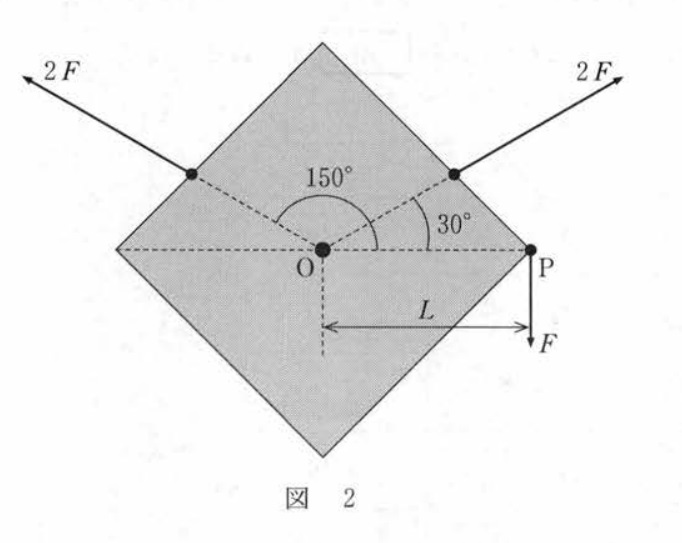
剛体の合力の問題です。図の3力を合成したものを選択肢から選びます。
剛体においては,剛体が変形しない理想的な物体のため作用線上で力を移動しても構いません。
まず上向きの $2F$ の2力をその作用線上で点Oまで移動させてから合成します。
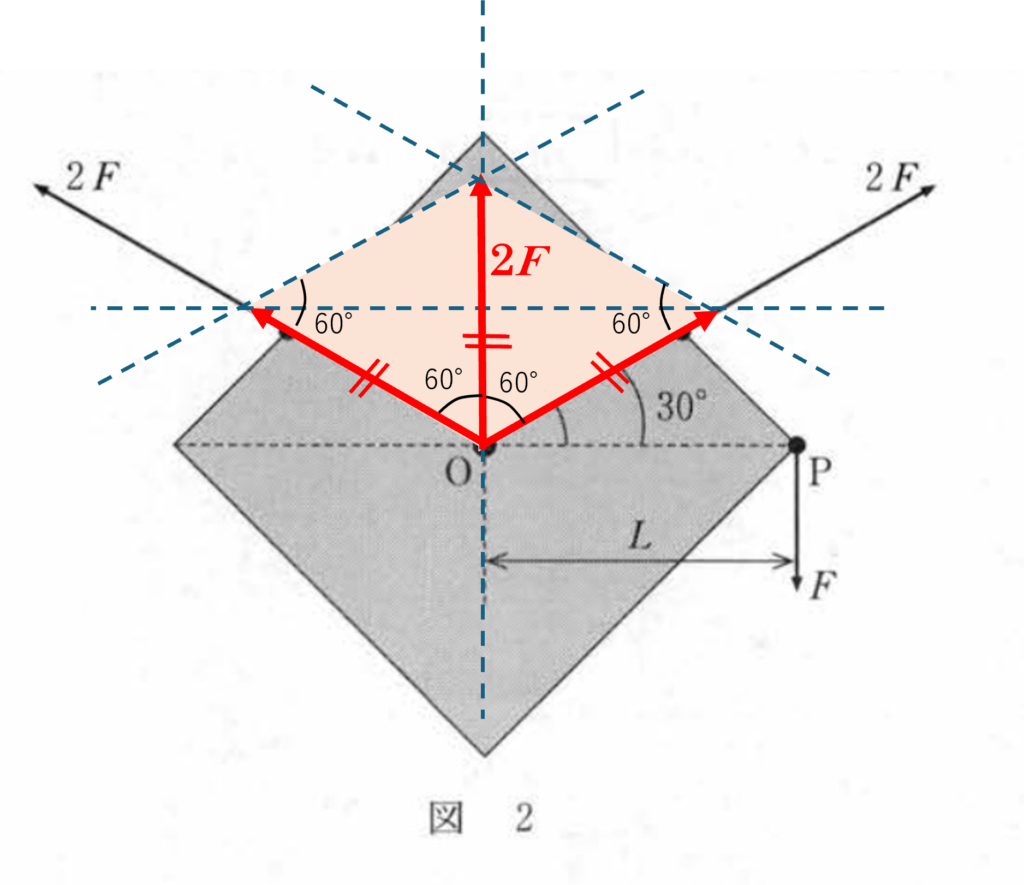
そうすると,都合の良いことに正三角形ができるので,これら2力の合力は大きさ $2F$ で,向きは図の向きです。
次に,この合力 $2F$ と $F$ を合成します。図の正方形の物体は考える必要はないので,次のように考えます。
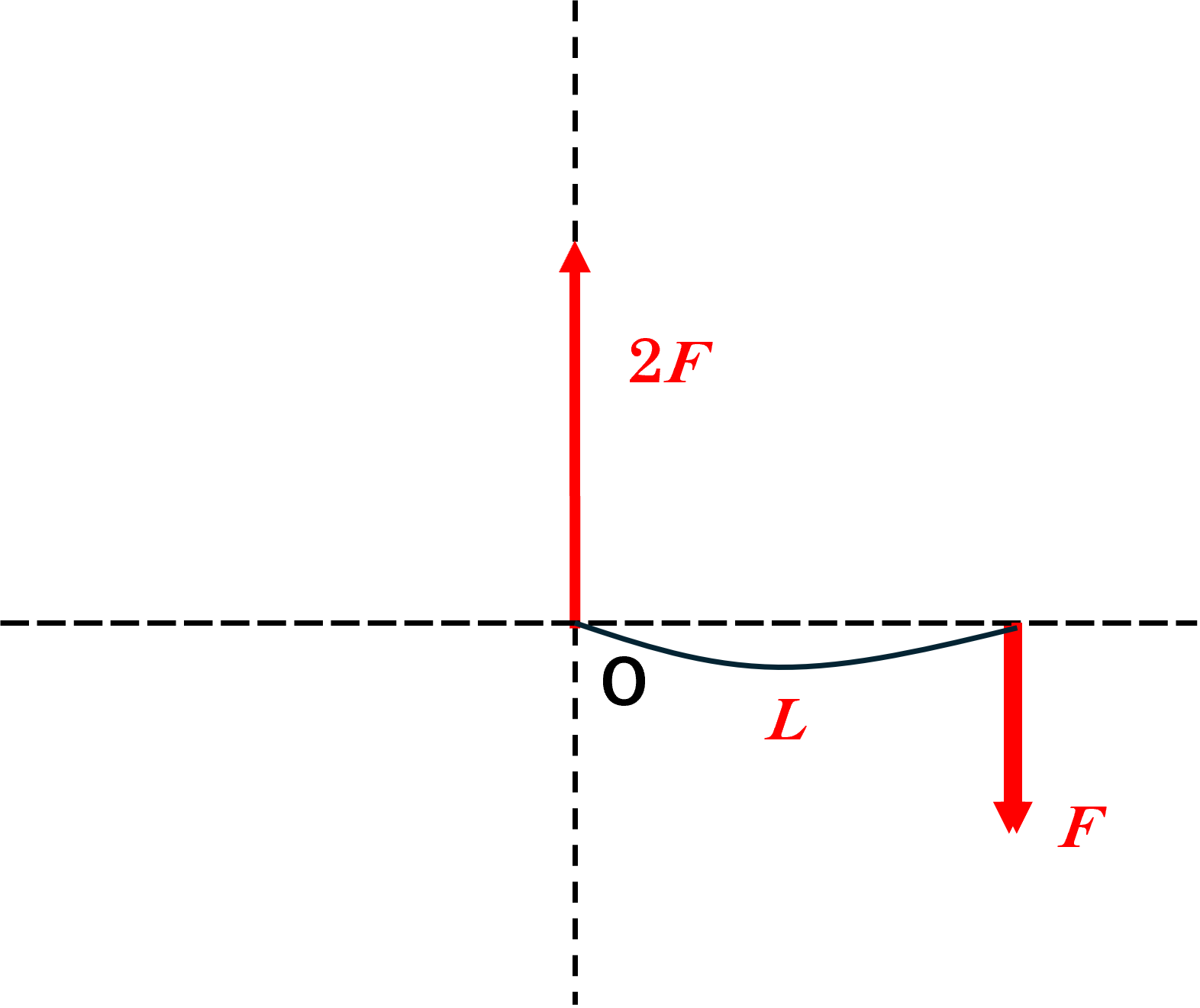
ここで考え方ですが,これらの力とつり合う力を考えると,次の図のように下向き O から左へ距離 $x$ のところに 大きさ $F$ の力( $2F-F=F$ )としてみます。そうして,O周りモーメントを求めます。
これらの力はつり合っているはずだから, $Fx-FL=0$ なので, $x=L$ になります。(そんなくどいこと考えなくても,ここでは見た目で $L$ ですが……考え方として)
$2F$ と $F$ の合力はこの力とつり合いますから,それは反対(上)向に大きさ $F$ であるはずです。
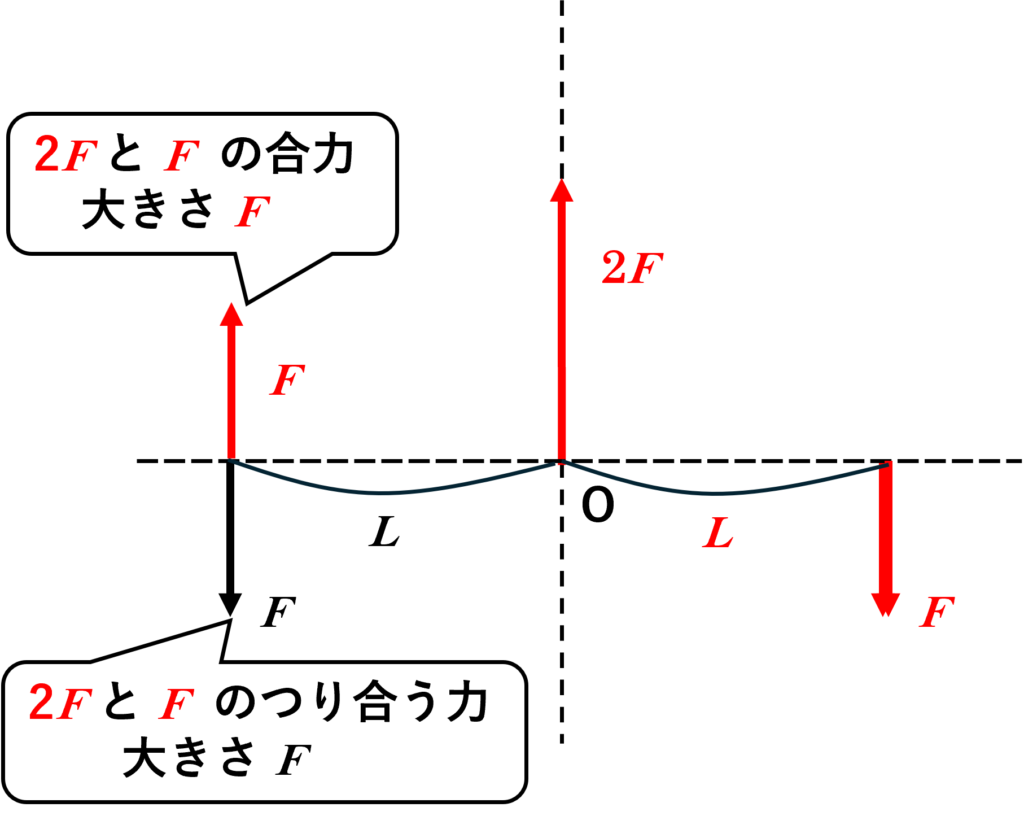
したがって,答えは 4 難易度 易
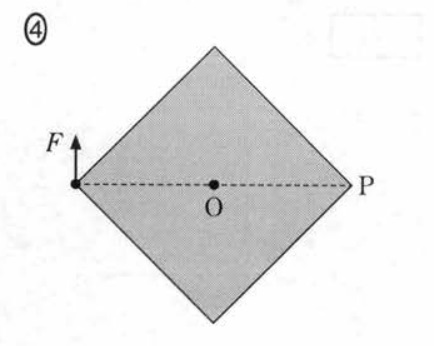

ちなみに,平行な力の合成についてはここで述べたような考え方がシンプルでおススメです。
問4
磁場のみ,磁場と電場の両方,電場のみ,がかかっている場合に,そこを通り抜けた荷電粒子の速さの大小を考えます。
図で 磁場のみ$v_3$,電場と磁場の両方 $v_1$,電場のみ $v_2$ とします。
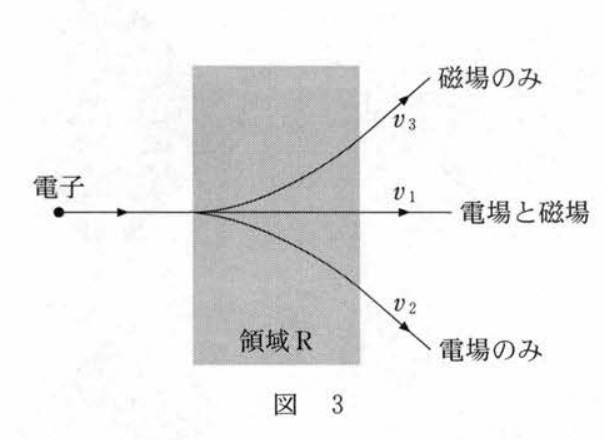
磁場のみの場合
「磁場は荷電粒子に仕事をしない」
なぜなら,運動する荷電粒子の進行方向に対して垂直に磁場からの力(ローレンツ力)がはたらくからです。($W=Fx$ で $x=0$ ということですね)
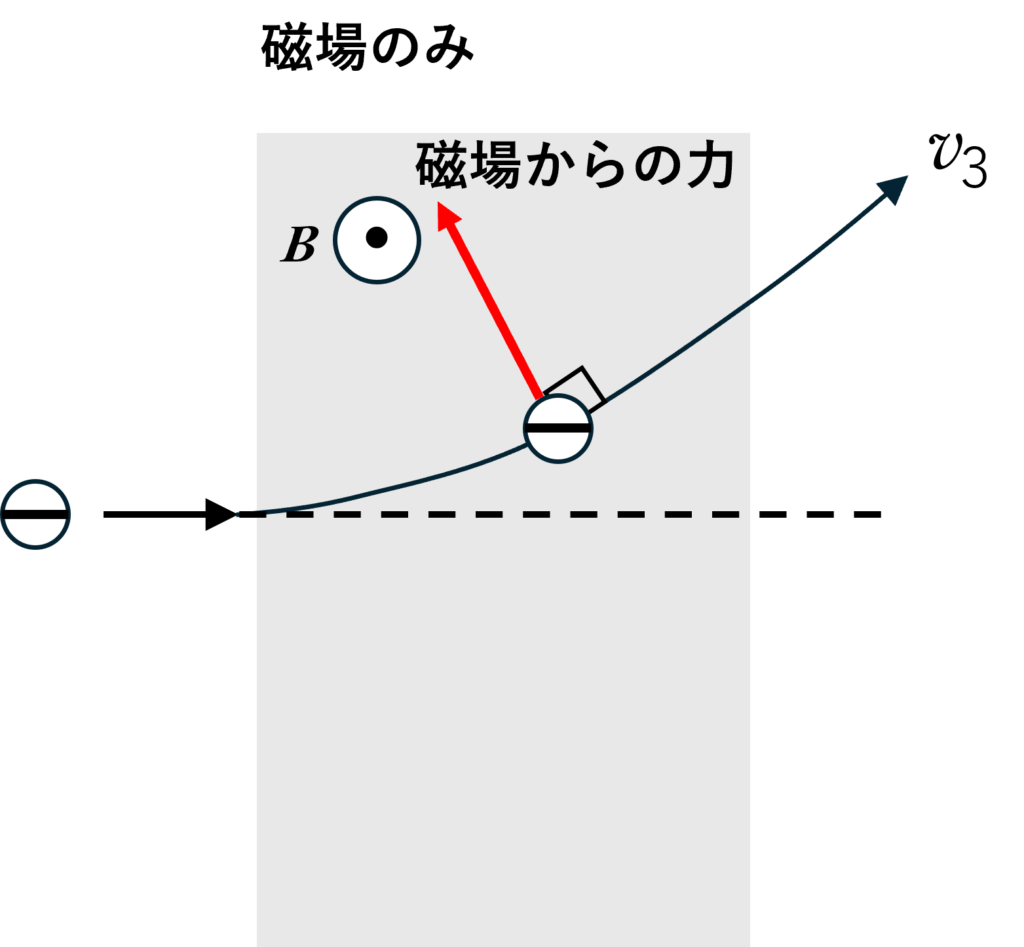
したがって,荷電粒子に磁場のみが働く場合には,荷電粒子は仕事を受けず,運動エネルギーは変化しません。よって速さ $v_3$ は電子の最初の入射の速さに等しくなります。
電場と磁場の両方が働く場合
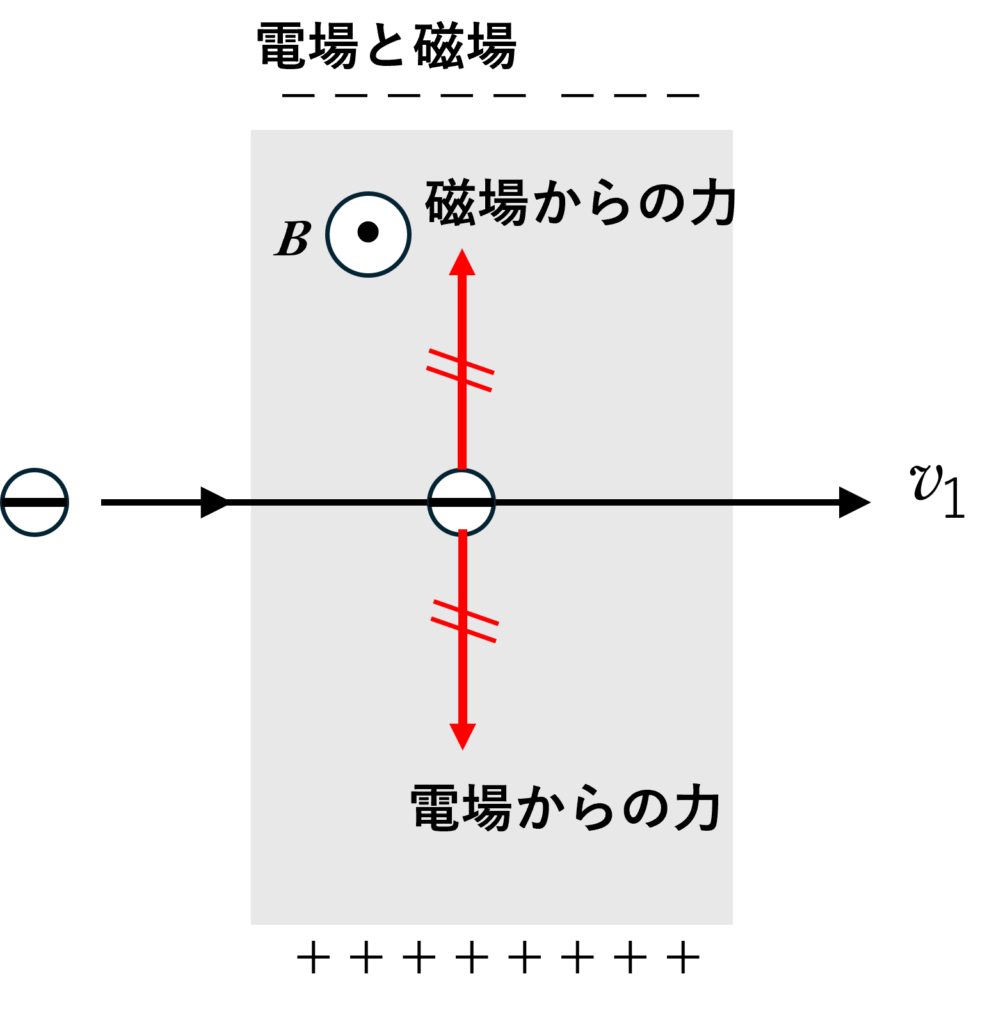
図より荷電粒子は直進しているため,荷電粒子にはたらく力は上図のようにつり合っていると考えられます。
したがって,荷電粒子の運動エネルギーは変化せず,速さ $v_1$ は電子の最初の入射の速さに等しくなります。
電場のみの場合
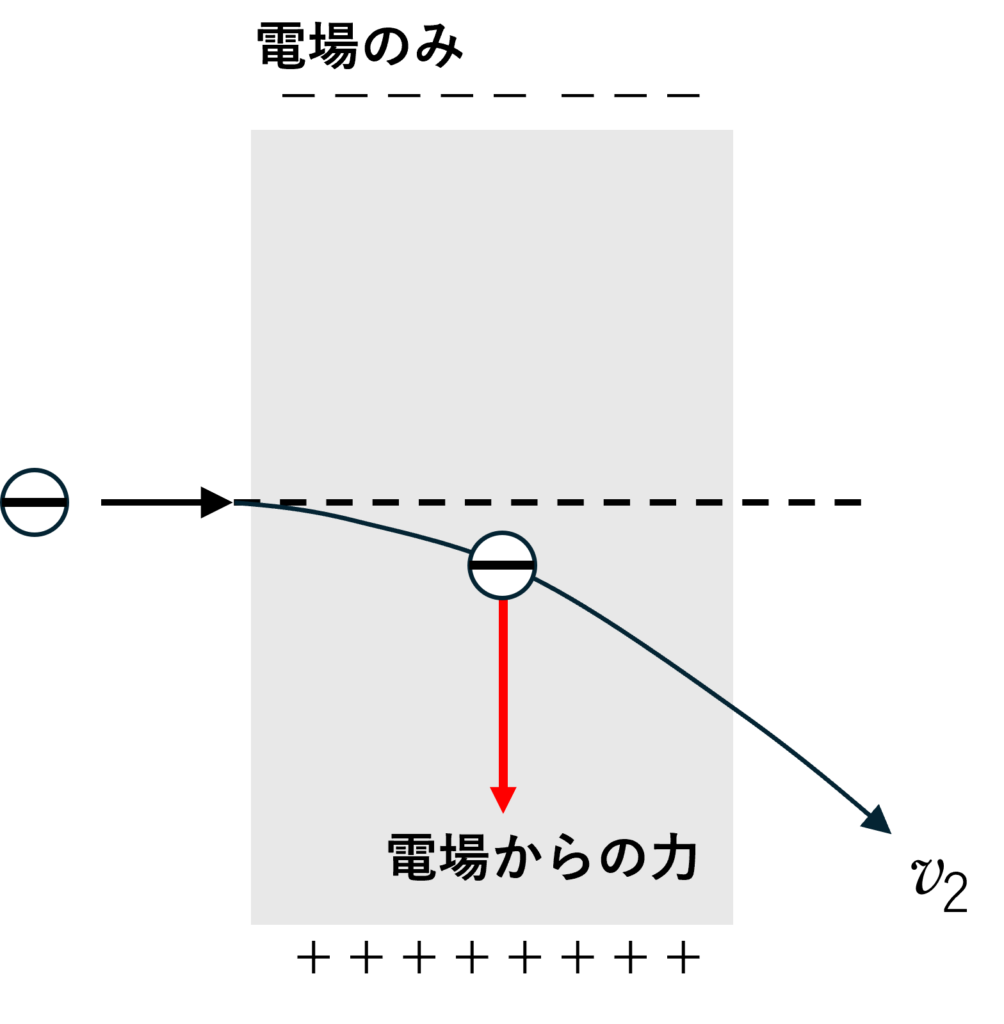
電場のみの場合,電場からの力は図のように常に図の上から下向きにはたらきます。この場合,荷電粒子の運動方向に対して垂直ではないため,荷電粒子は電場から仕事を受けて運動エネルギーが増加し,速さ $v_2$ は電子の入射の速さに比べると大きくなります。
以上より,
$v_2>v_3=v_1$
となります。
答え 2 難易度 易
問5
ド・ブロイの式とブラッグの反射条件を考えます。
ド・ブロイ波長 $\lambda$ は,質量 $m$ の電子(物質)が速さ $v$ で運動している場合に伴う波の波長です。光子のエネルギー $E$ ,光速 $c$ ,プランク定数 $h$ ,振動数 $\nu$ ,波長 $\lambda$ としたとき,光子の運動量 $p_c$ は,
$ p_c=\dfrac{E}{c}=\dfrac{h\nu}{c}=\dfrac{h}{\lambda}$
で示されます。
ここで,波動と考えられていた光子に運動量があるのなら,物体と考えられていた電子にも波動性があるとして,電子の運動量 $p_m=mv$ が次の式を満たすと考えます。
$p_m=mv=\dfrac{h}{\lambda}$
これより,$\lambda=\dfrac{h}{mv}$
となります。
次にブラッグの条件式ですが
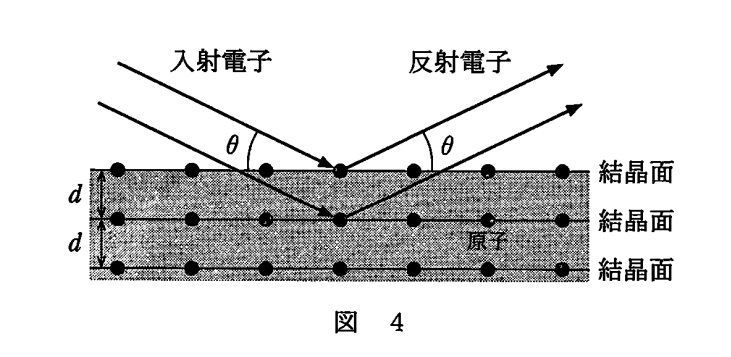
$2d \sin \theta =n\lambda$ $n=1,2,3 \cdots $
です。よって,最小角 $\theta_0$ のとき $n=1$ として
$2d \sin \theta_0 =\lambda$
より,ド・ブロイ波長 $\lambda=\dfrac{h}{mv}$ を代入して
$d=\dfrac{\lambda}{2 \sin \theta_0}=\dfrac{h}{2 mv\sin \theta_0}$
となります。
答え 5 難易度 易

この問題はド・ブロイの式を知っていれば簡単です。
知らなければ厳しいでしょう。
2つ目の問題はそれを代入するだけです。
個人的にはこのような問題はあまり良いとは思いません。
第2問
問1
単振り子の問題です。
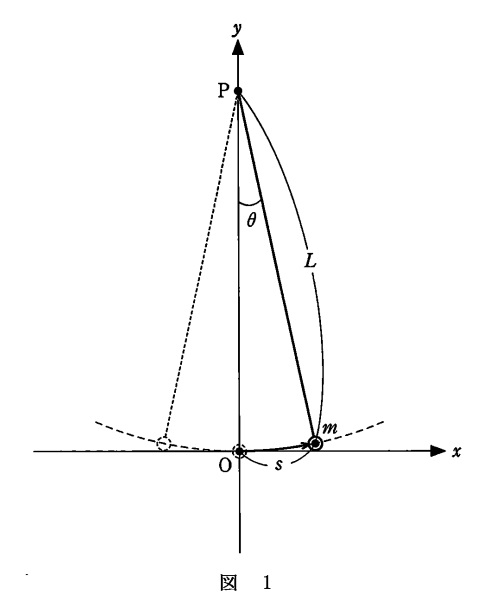
小球にはたらく運動方向の力 $F$ を求めます。
これは次の図(大げさに描いています)のように力を分解して考えればよいでしょう。
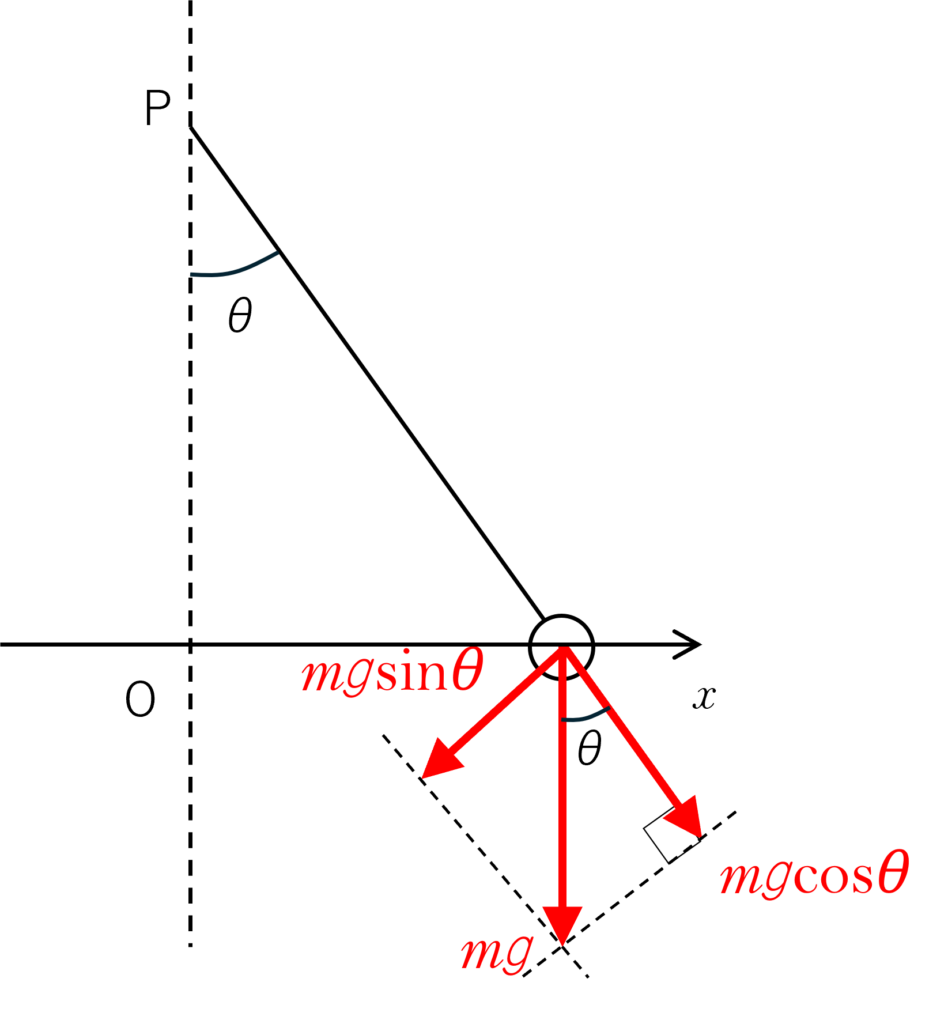
そうすると,方向を考えて $-mg\sin\theta$ ということになりますが,問題文より $\sin \theta \risingdotseq \theta$ より,
$-mg\sin\theta \risingdotseq -mg\theta $
答え 2 難易度 易

教科書的な問題ですね。
問2
単振り子の式について考えます。
小球の運動は点 O を中心とする振幅 $L\theta_0$ の単振動とみなすことから
単振動の式 $x=A\sin\omega t$ を考えます。
ここで,$s \rightarrow x$,$A \rightarrow L\theta_0$ であるから,
$s=L\theta_0 \times \sin \omega t$
また,
$\omega=\dfrac{2\pi}{T}$ $T=2\pi\sqrt{\dfrac{L}{g}}$
だから,
$\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{2\pi\sqrt{\dfrac{L}{g}}}=\sqrt{\dfrac{g}{L}}$
答え 1 難易度:易

なんだか,式を代入するだけ?
もうちょっとひねりが欲しいかも。
問3
単振り子での誤差について考えます。
実験で求めた周期が,$T_N=\dfrac{t_N}{N}$ で,$t_N$ 時間の正確な値より,$\Delta t \; (>0)$ だけ長いから,正しい時間を $t_0$ とすると,
$t_N=t_0 + \Delta t$
となります。周期の正しい値を $T_0$ とすると,
$T_0=\dfrac{t_0}{N}$
だから,$t_0=NT_0$ として,
$T_N=\dfrac{1}{T}(t_0 + \Delta t)$
$~~~~=\dfrac{1}{T}(NT_0 + \Delta t)$
$~~~~=T_0 + \dfrac{\Delta t}{N}$
$\Delta t > 0$ だから,$T_N>T_0$
よって,$T_N$ は周期の正しい値よりも,$\dfrac{\Delta t}{N}$ だけ大きいと見積もられる。
答え 5 難易度:易

文章を読んで式をたてみましょう。
問4
図のような装置で,振り子の周期を求める問題です。
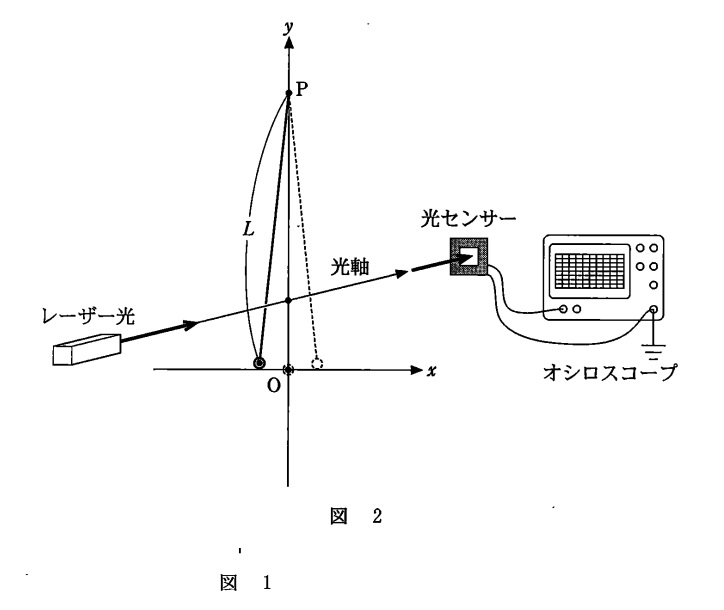
実験結果は次の図ようになりました。
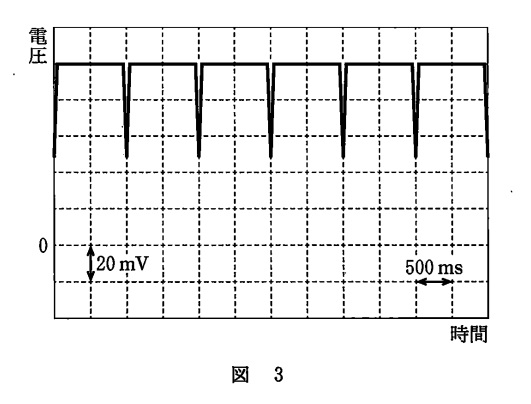
電圧が低くなる時は振り子の糸がレーザー光を遮るときだから,
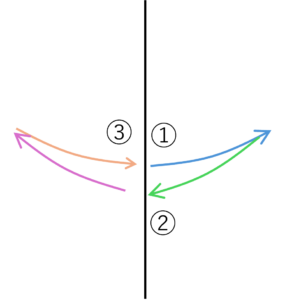
図の①~③で1周期と考えられます。したがって,次の図が正解となります。
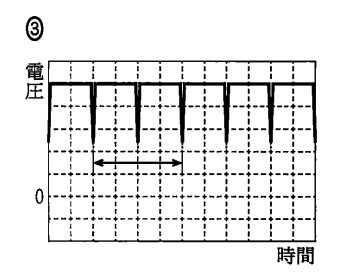
答え 3 難易度:易

これは簡単ですね。
勘違いしてミスしないように気を付けましょう。
問5
地球の自転が重力加速度に及ぼす影響について考えます。
極では遠心力の影響を受けないので,地球での重力加速度を $g$ とすると,
$mg_p=mg$
となります。
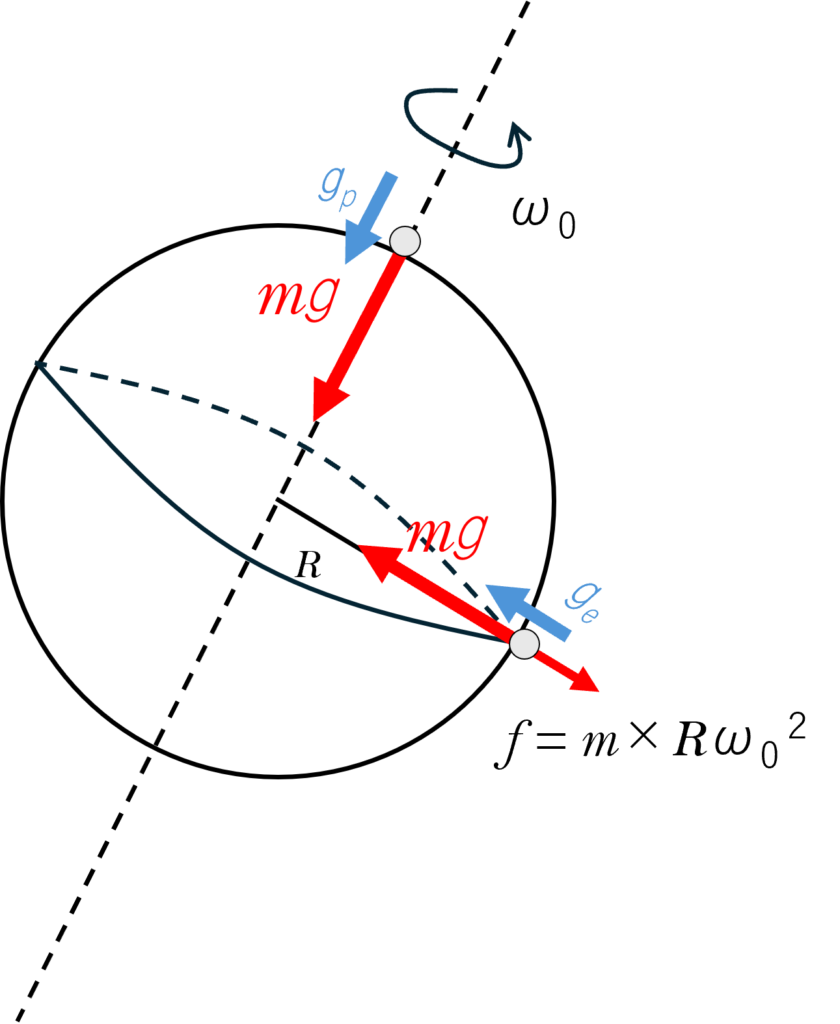
しかし,極以外では遠心力の影響を受けることに注意すると,赤道では最大の遠心力を受けることになります。
その大きさは,$f=mr\omega^2$ の式から
$f=m \times R\omega_0^2$
となります。したがって,図から赤道上での見かけの重力 $mg_e$ は遠心力の分だけマイナスして,
$mg_e=mg-f$
ここで,$mg=mg_p$ だから,
$mg_e=mg_p-f$
となります。ゆえに,
$g_e=g_p-\dfrac{1}{mf}$
答え 1 難易度 易

第2問は,どれもなんだか拍子抜けするような問題です。
共通テストのコンセプトはどこへ?
第3問
A
問1
図の A→B が定積変化 B→C が定圧変化 状態Aの温度が $T_\rm{A}$ 物質量 $n$ ,気体定数 $R$
A→B→C の変化において気体が外部にした仕事を求める,という問題です。
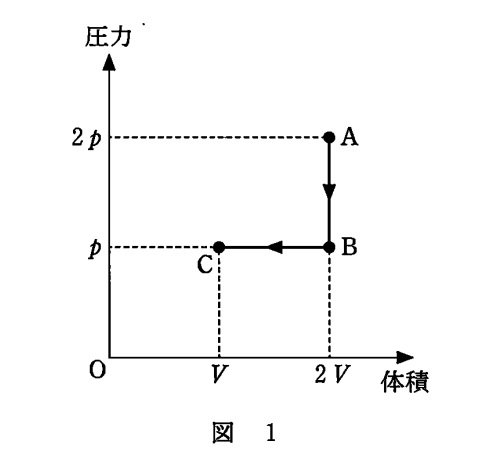
$W=p\Delta V$ だから,A→B→C の変化において,
A→B では $W_{\rm{AB}}=0$
B→C では $W_{\rm{BC}}=-p(V-2V)=-pV$
したがって,
$W=W_{\rm{AB}}+W_{\rm{BC}}=-pV$
また,$pV=nRT$ より状態 A においては,
$(2p)(2V)=nRT_\rm{A}$
$pV=\dfrac{1}{4}nRT_\rm{A}$
これらより
$W=-pV=-\dfrac{1}{4}nRT_\rm{A}$
答え ⑧ 難易度 易

基本的な問題ですね。
問2
A→B→C において,気体の温度を縦軸,体積を横軸として作成したグラフはどれか?という問題。

ここで,おさらいですが,図のように $p-V$ グラフでは斜め右上に行くほど温度が上がります。
なぜなら,$pV=nRT=kT$ ($k=nR$)より,$pV$ の値が大きいほど $T$ が大きくなるからですね。
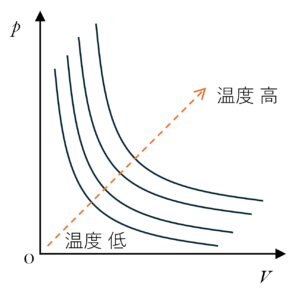
よって,次の図のように A→B→C と行くにつれて温度が低下するはずです。
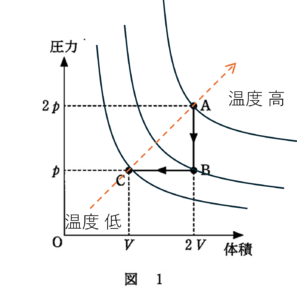
したがって,答えは②か④に絞られます。
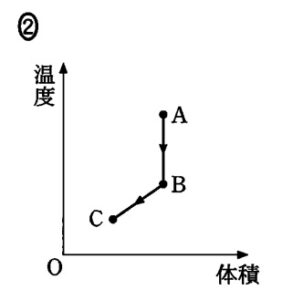
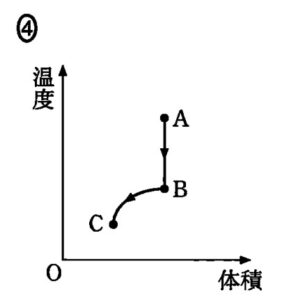
これらの図で異なるのは,B→C 過程です。ところで,B→Cは定圧変化ですから,$p$=一定 です。
$pV=nRT$ より,$T=\dfrac{pV}{nR}=kV \:\:\;\;\;\; (k=\dfrac{p}{nR}) $ ですから直線として変化し,原点に向かうことがわかります。
よって正解は②となります。
答え ② 難易度 普通

BC過程での $T-V$ グラフが原点を通るということは押さえておきましょう。
問3
逆に 過程I:C→B→A と変化させます。さらに図のような 過程II:C→A を考えます。
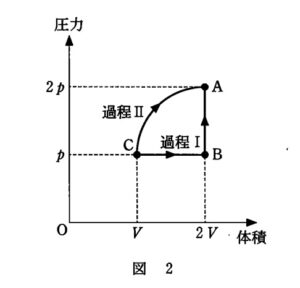
過程I,過程IIで
- 気体が外部にした仕事 $W_\rm{I}$ , $W_{\rm{II}}$
- 内部エネルギー変化 $\Delta U_\rm{I}$ , $\Delta U_{\rm{II}}$
とします。
1 仕事について

$pV$ 図において,pVグラフと横軸で囲む面積は仕事に等しくなります(図)。

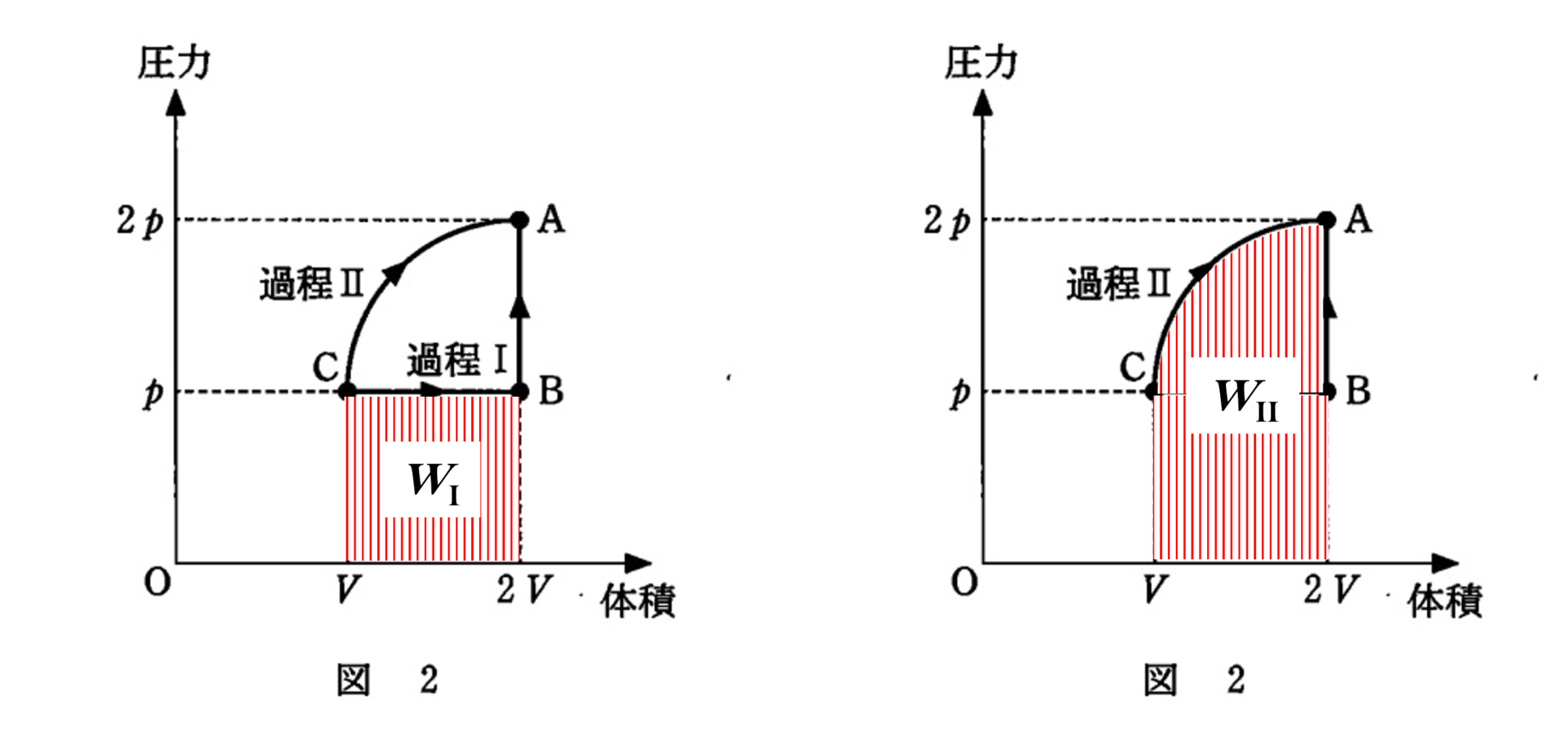
したがってこの場合は,$W_\rm{I} < W_{\rm{II}}$ となります。
2 内部エネルギーについて
$\Delta U=kT$ ($k$:比例定数)と,気体の内部エネルギー変化はその温度変化だけで決まります。
この場合,過程I,過程IIともに 状態C から ・状態A に到達することに変わりはありませんから,温度変化はどちらの過程を通過しても同じはずです。
したがって,$\Delta U_\rm{I} =\Delta U_{\rm{II}}$ となります。
外部から気体に加えられた熱量について
ここで,熱力学第1法則より,$Q=\Delta U + W $ から,
過程I,過程IIでの出入りする熱量をそれぞれ $Q_\rm{I}$ , $Q_{\rm{II}}$ とすると,
-
- 過程I:$Q_\rm{I}=\Delta U_\rm{I} + W_\rm{I}$
- 過程II:$Q_{\rm{II}}=\Delta U_{\rm{II}} + W_{\rm{II}}$
これと $W_\rm{I} < W_{\rm{II}}$, $\Delta U_\rm{I} =\Delta U_{\rm{II}}$ から,
$Q_\rm{I} < Q_{\rm{II}}$
したがって, $\Delta U_\rm{I} =\Delta U_{\rm{II}}$ かつ $W_\rm{I} < W_{\rm{II}}$, 過程II
答え ⑧ 難易度 普通

熱力学第1法則の式を立てて考えてみましょう。
B
波動の問題ですね。
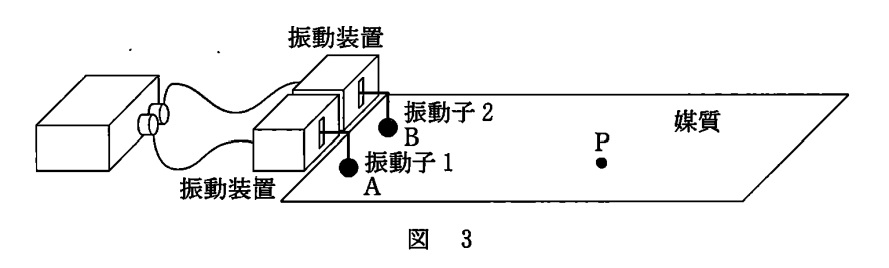
いろいろ記述されていますが,要約すると以下です。
- Aの時刻 $t$ における変位:$y_\rm{A}=a_0\sin (2\pi ft)$
- Bの時刻 $t$ における変位:$y_\rm{B}=a_0\sin (2\pi ft)$
- 振動数:$f$
- 振幅:$a_\rm{0}$
- Aからでた波が点Pに到達するまでにかかる時間:$t_{\rm{PA}}$
- Bからでた波が点Pに到達するまでにかかる時間:$t_{\rm{PB}}$
- Aからの波による時刻 $t$ での点Pにおける変位:$y_{\rm{PA}}$
- Bからの波による時刻 $t$ での点Pにおける変位:$y_{\rm{PB}}$
- Aからの波によるPの時刻 $t$ における変位:$y_{\rm{PA}}=a_{\rm{PA}}\sin \{2\pi f(t-t_{\rm{PA}})\}$
- 振幅:$a_{\rm{PA}}$
- Bからの波によるPの時刻 $t$ における変位:$y_{\rm{PB}}=a_{\rm{PB}}\sin \{2\pi f(t-t_{\rm{PB}})\}$
- 振幅:$a_{\rm{PB}}$
振動子1,2を同位相で振動させた場合の点Pにおける変位 $y_\rm{P}$ とすると,
$y_{\rm{PA}} + y_{\rm{PB}}=y_\rm{P} $
問4
図4は時刻 $t$ における変位 $y_{\rm{PA}}$ を示している。
この波の振動数と振幅を求めます。
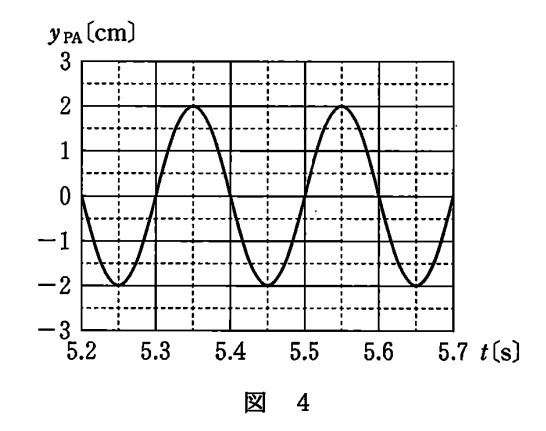
この波の周期 $T$ は,図より $T=5.5-5.3=0.2 $ s
したがって振動数 $f$ は,
$f=\dfrac{1}{T}=\dfrac{1}{0.2}=5 $ Hz
であることがわかる。
また振幅は図より,2 cm
答え ⑤ 難易度 易

これは簡単ですね。
問5
振動子1のみを振動させた場合の変位 $y_{\rm{PA}}$

振動子1と振動子2を同位相で振動させた場合の変位 $y_\rm{P}$
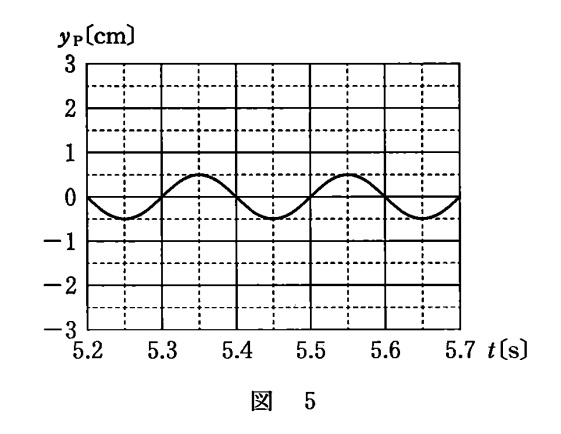
これらより振動子2のみを振動させた場合の点Pにおける変位を示すグラフを選びます。
これは次の図ように考えましょう。変位 $y_{\rm{PB}}$
振動子1,2を同位相で振動させた場合の点Pにおける変位 $y_\rm{P}$ とすると,
$y_{\rm{PA}} + y_{\rm{PB}}=y_\rm{P} $
であるので,

として,グラフを移項します。
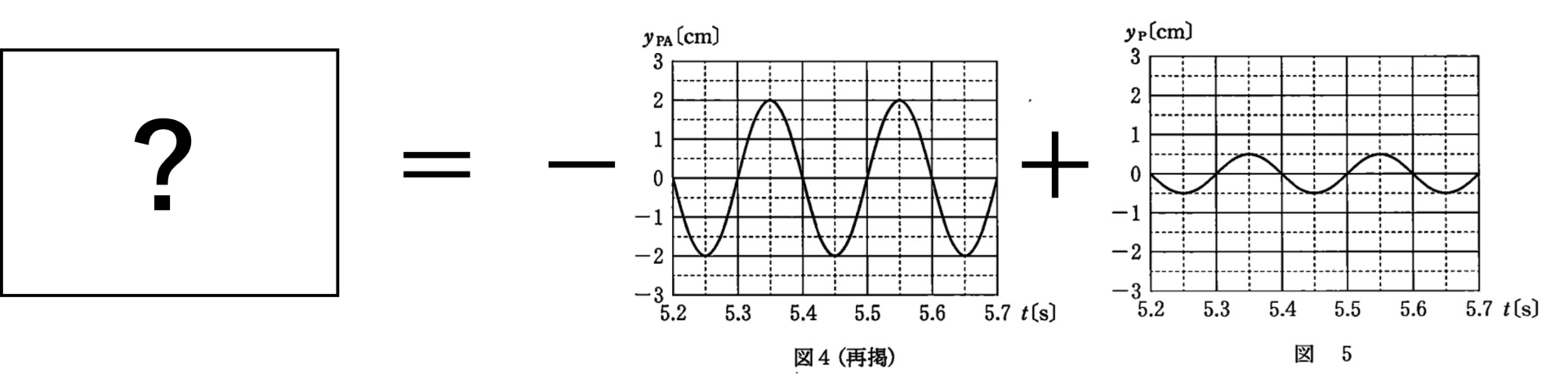
-がついているので上下反転します。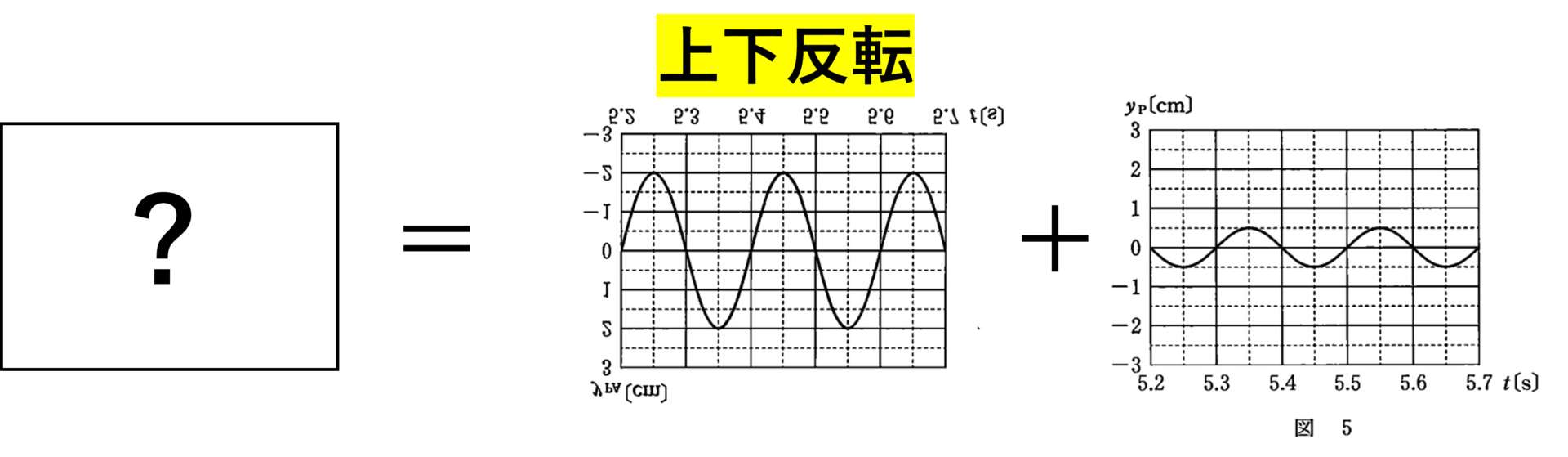
これは次のグラフ合成をすればよいことがわかります。
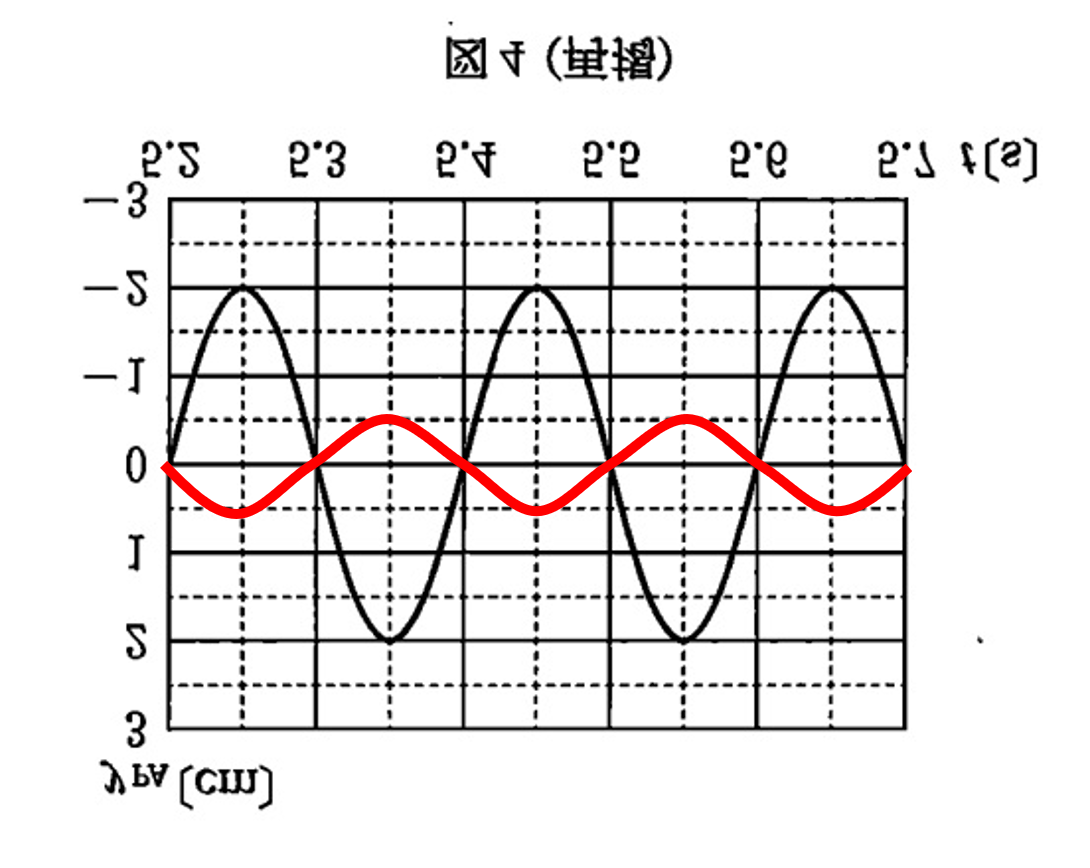
よって,答えは②
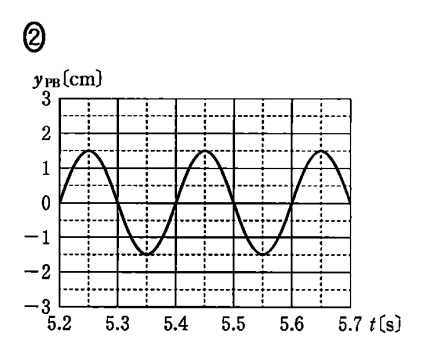
答え ② 難易度 普通

難しくはないのですが,あまり見かけない問題ですね。
問6
振動子1と振動子2を同位相で振動させます。
$ y_{\rm{PB}}=a_{\rm{PB}}\sin \{2\pi f(t-t_{\rm{PB}})\}$
でしたが,これを
$ y_{\rm{PB}}=a_{\rm{PB}}\sin \{2\pi f(t-t_{\rm{PA}}) + 2\pi f(t_{\rm{PA}} – t_{\rm{PB}})\}$
と変形しています。
問題では,波源Aから出た波と波源Bから出た波が点Pで最も強め合うためには,$f(t_{\rm{PA}} – t_{\rm{PB}})$ が整数でなければならない,としています。
この意味を考えてみましょう。
同位相で波源Aから出た波と波源Bから出た波が最も強め合うためには,それぞれの変位 $ y_{\rm{PA}}$ と $ y_{\rm{PB}} $ について,時間 $t$ にかかわらず,
$ y_{\rm{PA}}=k \times y_{\rm{PB}} $
であればよいということになります。($k$:Pの位置による定数)
つまり点Pにおいては,Aからの波とBからの波がいつも同じ位相で到達する,ということになります。

$k$ を入れたのは $a_{\rm{PA}} $ と $a_{\rm{PB}}$ が場所により,それらが同じとはかぎらないからです。
点PがA,Bから等距離にある位置ならば $k=1$ となります。
よって,
$ y_{\rm{PA}}=a_{\rm{PA}}\sin \{2\pi f(t-t_{\rm{PA}})\}$
$~~~~~~= k\times a_{\rm{PB}}\sin \{2\pi f(t-t_{\rm{PA}}) + 2\pi f(t_{\rm{PA}} – t_{\rm{PB}})\}$
$~~~~~~=k\times y_{\rm{PB}} $
ということですから,位相部分である $\{2\pi f(t-t_{\rm{PA}})\}$ と $\{2\pi f(t-t_{\rm{PA}}) + 2\pi f(t_{\rm{PA}} – t_{\rm{PB}})\}$ に注目します。
三角関数の位相ですから位相が $2\pi$ 変化するごとに同じ値になることに注意すると,$2\pi f(t_{\rm{PA}} – t_{\rm{PB}}) $ が $2\pi$ の整数倍であれば,Aからの波とBからの波の点Pにおける位相が同じになることに気が付きます。
したがって,波源Aから出た波と波源Bから出た波が点Pで最も強め合うためには,$ f(t_{\rm{PA}} – t_{\rm{PB}})$ が整数でなければならない,というわけです。

ややこしいことを言わなくても,最初から,
点Pでそれぞれの波の位相が同じになる必要がある,でいいですね。
長くなりましたが,本題に入りましょう。
-
振動子1と振動子2の振動数を $8.0$ Hz ,同位相で振動させる。
-
波のつたわる速さを $4.0$ m/s とする。
とした場合,
点PでAからとBからの波が最も強め合う場合の,$|t_{\rm{PA}}-t_{\rm{PB}}|$ と $|\rm{AP}-\rm{BP}|$ の値を求めよ,という問題です。
問題文にあるように,$ f(t_{\rm{PA}} – t_{\rm{PB}})$ が整数でなければならないという条件から
$ f|t_{\rm{PA}} – t_{\rm{PB}}|=8.0 \times |t_{\rm{PA}} – t_{\rm{PB}}|$
が正の整数になればいいですね。この条件に合うのは回答欄では $|t_{\rm{PA}} – t_{\rm{PB}}|=0.50$ s のみです($ 8.0\times 0.50=4.0 $)。
次に,時間と速さ,距離の関係から
$t_{\rm{PA}}=\dfrac{\rm{AP}}{v}=\dfrac{\rm{AP}}{4.0}$
$t_{\rm{PB}}=\dfrac{\rm{AP}}{v}=\dfrac{\rm{BP}}{4.0}$
よって,
$|\rm{AP}-\rm{BP}|=4.0\times |t_{\rm{PA}}-t_{\rm{BA}}|=4.0\times 0.50 =2.0$ m
答え ⑤ 難易度 普通

問題文にある式を見て?? となった人もいるかもしれませんが,
指示されたようにすれば解けるようになっていますね。
個人的にはそういう問題はあまり好きではありませんが …。
第4問
電磁気の問題です。
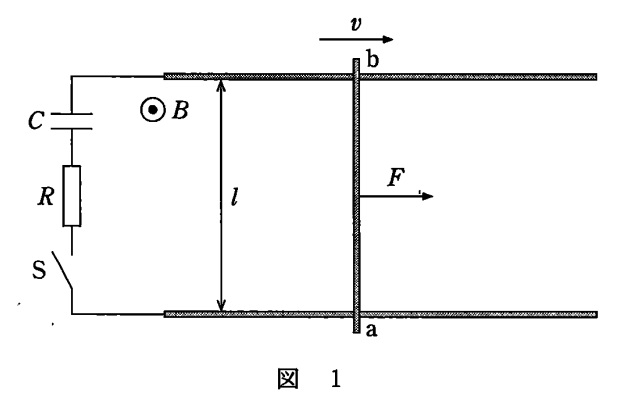
次のような操作をします。
- はじめにコンデンサーに電荷はない。
- スイッチSは開いている。
- 導体棒を図の右向きに一定の速さ $v$ で動かしながらSを閉じる。
- Sを閉じた後も導体棒に力 $F$ の外力を加え続けて,導体棒を等速 $v$ で右に動かす。
問1
導体棒が右向きに速さ $v$ で動くときに導体棒のab間に生じる誘導起電力 $V_1$ の大きさを考えます。
これは,おなじみの式 $V=vBl$ そのままですね。
$V_1=vBl$

これは バーベル($vBl$) は 起電力($V$) と覚えましょう。
Sを閉じた直後に導体棒に流れる電流の向きについては,右手の法則を考えてみましょう(他にも左手の法則を使って電子の動きを考えてもいいでしょう)。
閉回路を考えて,それを貫く $B$ の変化を妨げる向きに磁場を作ろうとする向きに電流が流れます。
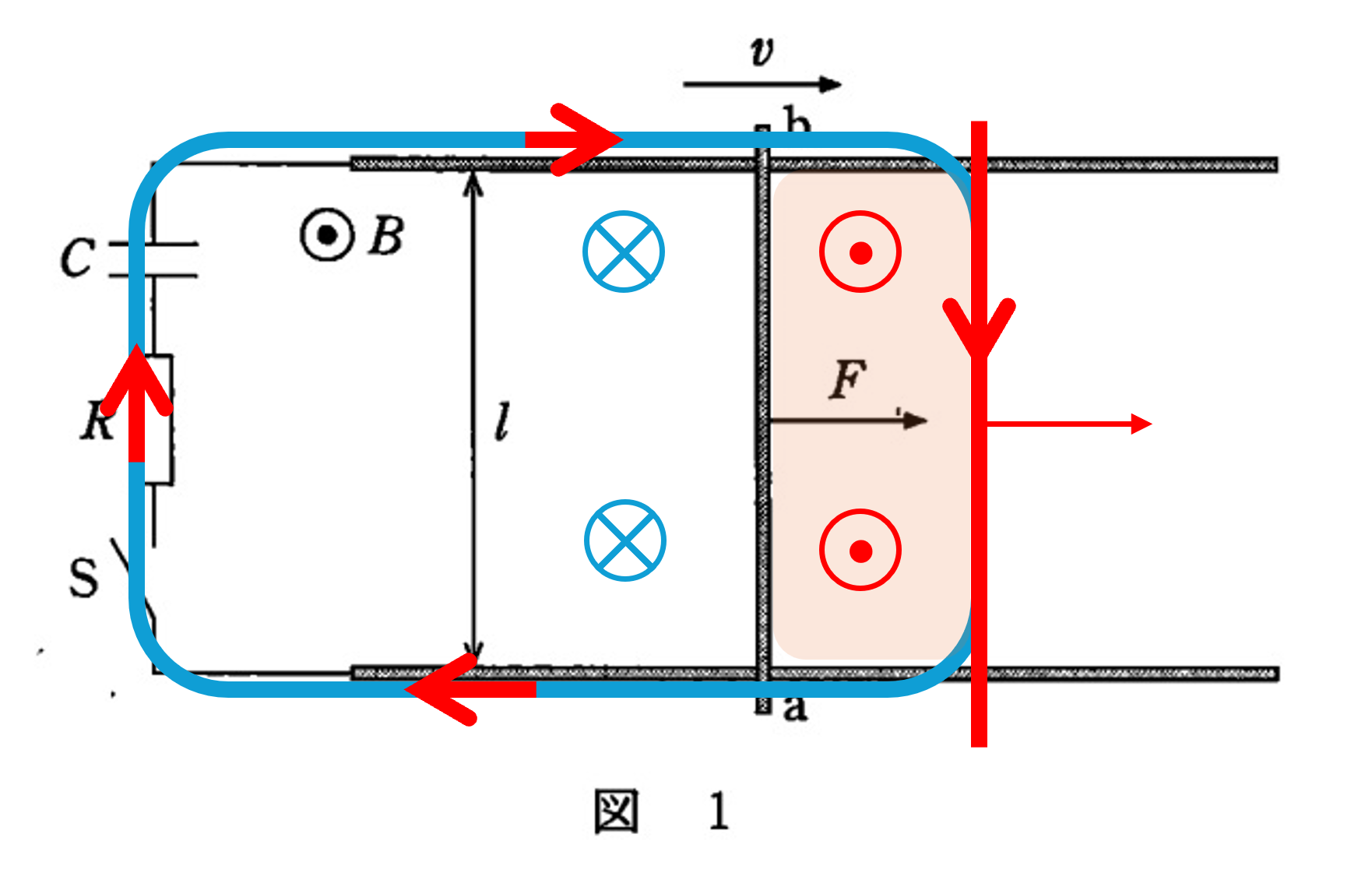
図で,導体棒が移動すると閉回路において,薄オレンジの部分の面積が増えます。
そうすると,その部分の赤色の $B$ が増加することになります。
そのため,逆向きの水色の $B$ を作る方向に誘導電流が流れます。
親指をたてて軽く握ったこぶしを作ります。
親指を水色の $B$ の方向に向けたとき,指の方向が誘導電流の向きになります。
したがって,誘導電流の向きは b→a の向きです。
答え ⑥ 難易度 易
問2
Sを閉じてから時間がたつにつれて,導体棒に加える力 $F$ はどのように変化するのか考えます。
もう一度回路を見直すと,この回路にはコンデンサーが含まれています。導体棒に電流が流れるのはコンデンサーが充電されるまでの間です。コンデンサーがフル充電されてしまえば,コンデンサーは絶縁と同じ状態となり,回路に電流は流れません。
力 $F=IBl$ だから,十分に時間がたった時には $I=0$ となり,力 $F$ は 0 になっていくと考えられます。
そのようなグラフは,①と④だけです。この場合,変化は直線的にはならないことを考えて①が答えです。

$F=IBl$
$BIl=F$ ビール($BIl$)は力($F$)と覚えましょう。
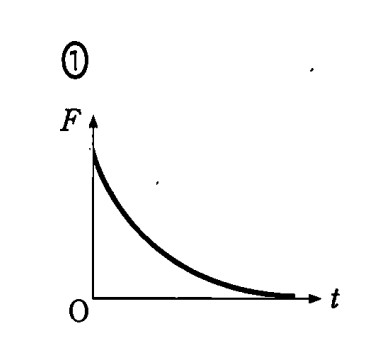
答え ① 難易度 普通
上に記したように $F$ と $t$ のグラフは,$F=IBl$ より,$I$ と $t$ のグラフと同じような形になるはずです。
この場合の,力と時間のグラフや電流と時間のグラフが直線にはならないのは,直感的にもそう思えますが ……。
とりあえずこの回路に関してキルヒホッフの法則の式を立ててみます。導体棒を一定の速さで引くため $vBl$ は定数で,$E=vBl$ ,また $Q=CV$ ,$\sum E = \sum RI$ より
$ vBl=RI + \dfrac{Q}{C}\:\:\:\: \cdots\cdots $ (a)
ここで $t=0$ のときに $Q=0$ だとすると,初期の電流値を $I_0$ として
$vBl=RI_0$
より,
$I_0=\dfrac{vBl}{R}$
です。ここで,(a) より,
$Q=C(vBl – RI )$
電流は $I=\dfrac{dQ}{dt}$ だから,
$I=\dfrac{dQ}{dt}=\dfrac{d}{dt}\{ C(vBl – RI) \}=-RC\dfrac{dI}{dt}$
$\dfrac{dI}{I}=-\dfrac{1}{RC}dt$
より,両辺を積分して
$\displaystyle\int{\dfrac{dI}{I}}=\displaystyle\int{\left (-\dfrac{1}{RC} \right ) dt} $
$\log I = -\dfrac{1}{RC}t + K$ ( $K$:積分定数 )
$I = e^{-\dfrac{1}{RC}t + K }$
ここで,$t=0$ のとき $I=I_0$ だったから,
$I=I_0e^{-\dfrac{1}{RC}t}$
この $I$ は直線的ではなく曲線的に変化します。
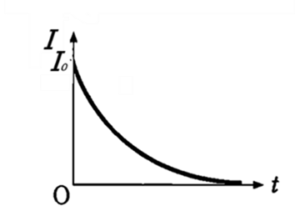
となると力は $F=IBl $ なので,同様に力と時間のグラフも曲線的に変化します。

最初はコンデンサーに電荷がないため,コンデンサーを導線とみなすと電流がドカンと流れますが,充電が進むにつれだんだん流れなくなる …… という感じでいいと思います。
問3
Sを閉じてから十分に時間が経過するまでに(コンデンサーにフル充電されるまでに),
- 外力がした仕事の大きさ:$W$
- 抵抗で発生したジュール熱の大きさ:$J$
- 十分な時間がたったときにコンデンサーに蓄えられているエネルギー:$U$
ここで,$W$,$J$,$U$ の間の関係式を求めます。
ここは,エネルギー保存則から
$W=J+U$
でいいでしょう。よって解答に合わせると,
$W-J-U=0$
答え ④ 難易度 易

これは易しいと思いますが,勘違いしないように気を付けましょう。
次に,
外力がした仕事の大きさ $W$ は,十分な時間がたったときにコンデンサーに蓄えられている電荷を, 導体棒の両端に生じる電位差 $V_1$ に逆らって運ぶ仕事の大きさに等しくなる。
との記述があります。これは,十分な時間がたったときにコンデンサーに蓄えられている電荷を $Q_1$ とすると,仕事 $W=Q_1V_1$ であったということを示しています。
したがって,$Q=CV$ より,
$W=Q_1V_1=CV_1^2$
問題は,このときに抵抗で発生したジュール熱の大きさ $J$ を求めます。
コンデンサーに蓄えられているエネルギーは $U=\dfrac{1}{2}CV_1^2$ だから,これらを先ほどの式 $W-J-U=0$ に代入します。
$W-J-U=CV_1^2-J-\dfrac{1}{2}CV_1^2=0 $
より,
$J=\dfrac{1}{2}CV_1^2$
答え ② 難易度 普通

電池をつないだ回路では,
コンデンサーに充電するとき,電池のする仕事の半分のエネルギーしかコンデンサーにたまりません。
あとの半分はジュール熱で消えてしまいますね。これを知っていたらすぐに答えがわかります。
なぜって, コンデンサーに$Q$ の電荷がたまるとき,電池のする仕事は $QV$ だけど,コンデンサーにたまるエネルギーは,$\dfrac{1}{2}QV$ で半分だけですからね。
この問題で言っていることはこういう意味のことですね。
問4
Sを閉じてから十分な時間が経った後に(コンデンサーにフル充電した後に),Sを開いて導体棒を静止させ,続いて再びSを閉じます。
Sを閉じた直後に導体棒に流れる電流の向きと導体棒の運動を考えます。
これは,コンデンサーにフル充電したエネルギーを使って導体棒に電流を流すと考えればよいでしょう。
つまり,フル充電したコンデンサーは,Sを再び閉じた直後は図のような極性をもつ電源として考えればよいということです。
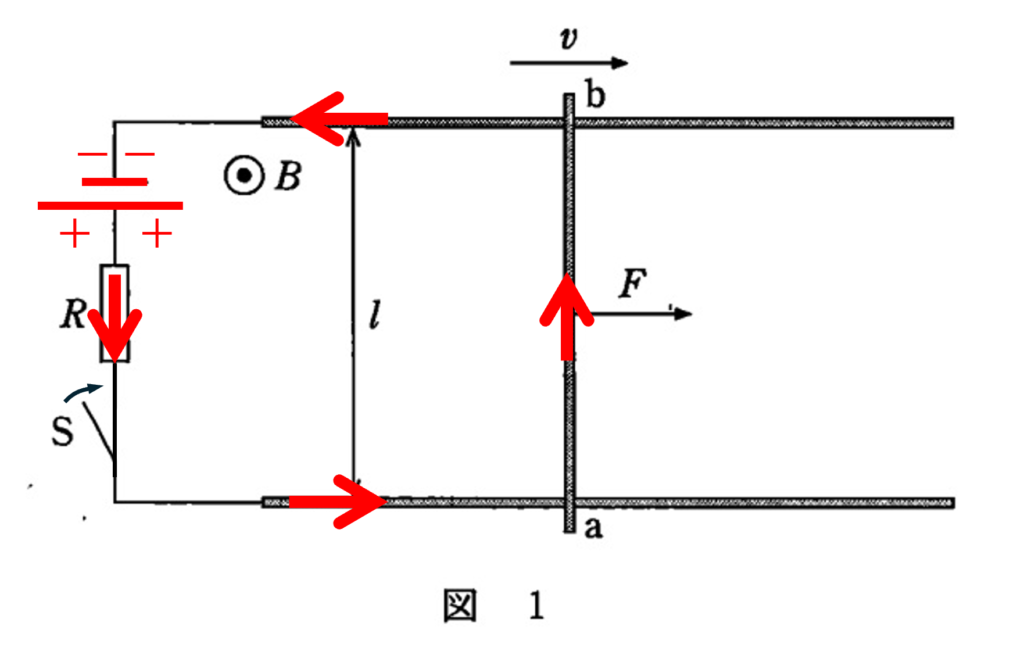
図より電流の方向は a → b ということになります。
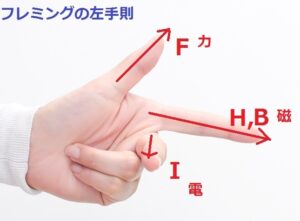
また,導体棒には「フレミングの左手則」から力は図の右方向にはたらきます。
答え ⑥ 難易度 易

フレミングの左手則
問5
今度はコンデンサーの代わりにコイル(インダクタンス:$L$)を用います。
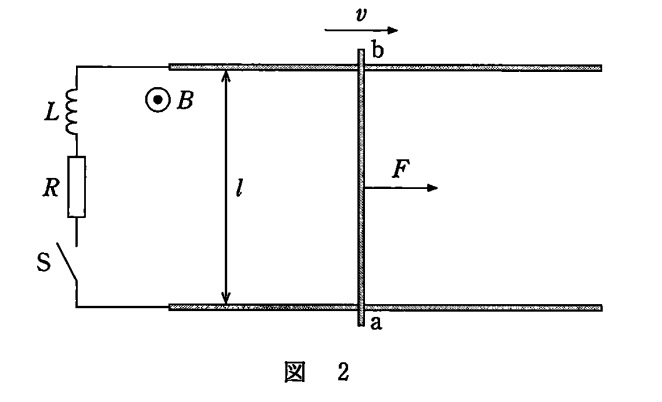
同様に導体棒を速さ $v$ で移動し続けるように,力 $F$ で引きます。
このときの導体棒に生じる誘導起電力を $V_2$ とします。
Sを閉じてから時間 $t$ だけ経ったときの,回路を流れる電流 $I$ のグラフは下図のようになりました。
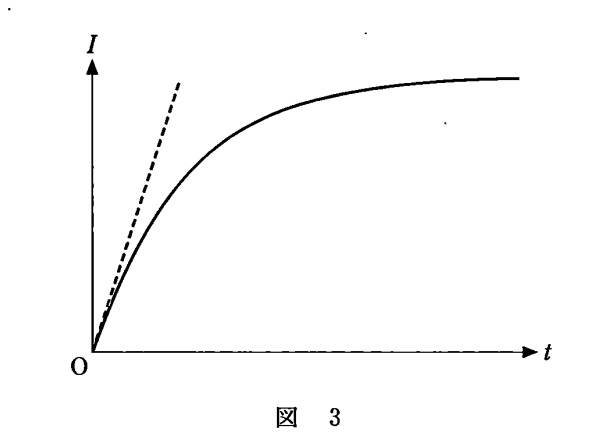
Sを閉じてから十分に時間が経ったときの,コイルに発生する誘導起電力の大きさを表す式を考えます。
コイルに発生する誘導起電力ですから,定常状態では 0 です。
なぜなら,コイルに発生する誘導起電力 $V$ は,
$V=\left | L\dfrac{\Delta I}{\Delta t} \right |$
で示されますが,時間が十分に立った場合の $\dfrac{\Delta I}{\Delta t} =0 $ となるためです。
答え ⑦ 難易度 易

コイルに発生する誘導起電力…
ですから,間違えないように注意
問6
Sを閉じてから時間 $t$ だけ経ったときの,$F$ を表すグラフを考えます。
導体棒は等速で運動するため,導体棒を引く力 $F$ と磁場からの力 $IBl$ はつり合っています。
また,コイルの特性として逆起電力を発生しますから,回路を流れる電流は 0 からだんだんと大きくなっていきます(図3)。
そのため,力 $F$ も図3と同じように増加していきます。
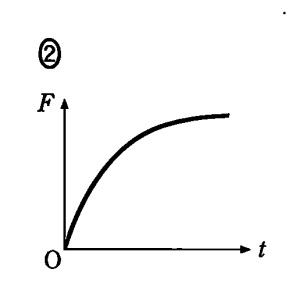
答え ② 難易度 易
問7
$I-t$ 図の傾きを $a$ とします。
コイルの自己インダクタンス $L$ を表す式を考えます。

コイルに発生する誘導起電力 $V$ は,
$V=\left | L\dfrac{\Delta I}{\Delta t} \right |$
で示されます。時刻 $t=0$ の近くにおける電流 $I$ の時間変化の様子は,図の破線で近似できるとあります。
よって,
$ \dfrac{\Delta I}{\Delta t}=a $
また,問題文から,「導体棒の両端に生じる誘導起電力を $V_2$ とする」より,$t=0$ ,$I=0$ では,コイルの誘導起電力が導体棒の発生する誘導起電力の大きさに等しいので,
$V_2=\left | L\dfrac{\Delta I}{\Delta t} \right |=La $
ゆえに,
$L=\dfrac{V_2}{a}$
答え ④ 難易度 普通






































コメント