物理のエッセンス電磁気編52番のダイオードを含む回路について詳しく解説します。
エッセンス 電磁気 52番 P85 ダイオード
物理のエッセンス 電磁気編 の85ページ 52番を参照してください。
ダイオードの特性
基本的にはダイオードというものは電流を一方向だけへ流す作用をもつものです。
(違う用途のダイオードもありますがここでは割愛します)
ダイオードそのものについては、こちらの記事で解説していますので参考にしてください。
また、この問題(52番)では、ダイオードでの電圧降下は0としています。
動画
電磁気 52番 問 (1)
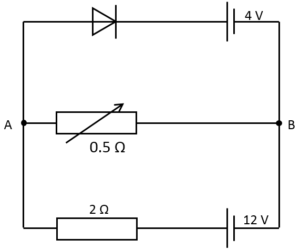
このときのAB間を流れる電流を計算しましょう。
まず次の図で回路の下側の閉回路について注目します。
ダイオードはとりあえず断線と仮定します。
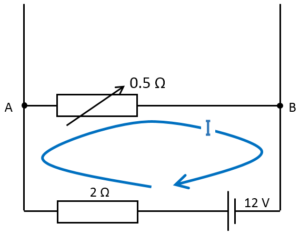
このとき、キルヒホッフの法則より、
$12=2\times I + 0.5 \times I$
$I=4.8 \:A$
もし断線しているなら、AはBよりも $V=RI=0.5\times 4.8=2.4\:V$ 高いことになります。
ちなみに、$2\:\Omega$ 抵抗での電圧降下は、$V=RI=2\times 4.8=9.6\:V$ ですね。
このときの図をイメージ的に示すと次図のようになります。
回路を縦に書き直し、アースを追加して最下端を $0\:V$ とみなしています。
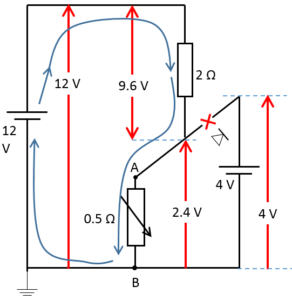
となると、電流は電位の高い方から低い方へ流れるため、
図では青の矢印の方に電流が流れるのが自然です。
したがって、ダイオードの順方向には電流が流れることはありません。
また、$4\:V$ 電池からの電流はダイオードに阻止されるため、これも流れることはなく、結局、ダイオードと $4\:V$ 電池を含む図の右の回路は断線と同じと判断されます。
よって、AB間の電圧は、$2.4\:V$ 、電流は $4.8\:A$ ということになります。
電磁気 52番 問 (2)
では問題の(2)です。
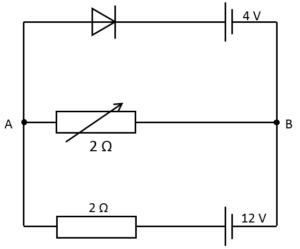
このときのAB間を流れる電流を計算しましょう。
まず次の図で回路下側の閉回路について注目します。
ダイオードはとりあえず断線と仮定します。
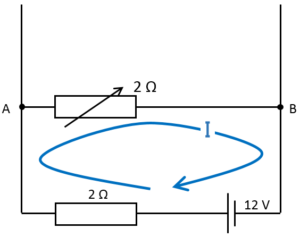
このとき、キルヒホッフの法則より、
$12=2\times I + 2 \times I$
$I=3 \:A$
もし断線しているなら、AはBよりも $V=RI=2\times 3=6\:V$ 高いことになります。
ちなみに、$2\:\Omega$ 抵抗での電圧降下は、$V=RI=2\times 3=6\:V $ です。
(まあ、そんなこと言わずとも、$12\:V$ を $2\:\Omega$ の抵抗2つですから、片方 $6\:V$ ですね)
このときの図をイメージ的に示すと次図になります。
回路を縦に書き直し、アースを追加して最下端を $0\:V$ とみなしています。
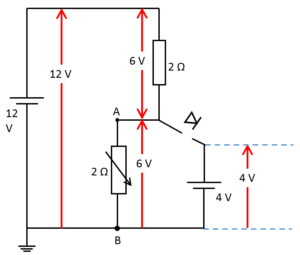
今はまだ、ダイオード部を断線で考えています。
このとき、A点は $6\:V$ の電位をもちますが、$4\:V$ 電池の方は断線の手前で $4\:V$ の電位を持ちます。
もしこれをつなぐと、電流は電位の高い方から引く方へ流れるため、図の $4\:V$ 電池に対して電流が逆流します。
また、このときのダイオードの順方向は、この場合電流の流れを阻止しません。
したがって、これはダイオードを単なる導線と考えてもう一度仕切り直しです。
注意ですが、この場合、電池を含めて回路を考え直すため、実際のAB間の電圧は $6\:V$ とはなりません。
では、次図の青い線で示された閉回路での、キルヒホッフの法則を考えます。
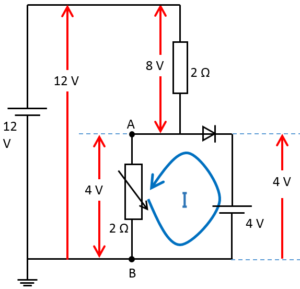
$4=2\times I$
$I=2\:A$
ちなみに、AB間の電圧降下 $V$ は、 $4\:V$ 電池の電圧に等しいため $4\:V$ です。
また、次の図のような青い線で示されたキルヒホッフの閉回路を考えた場合、
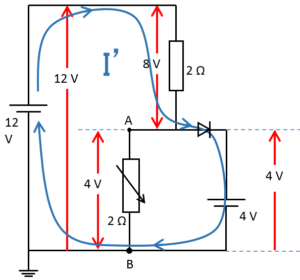
流れる電流を $I’$ とすると、
$12-4=I’\times 2$
$I’=4\:A$
となり、図の上にある $2\:\Omega$ 抵抗を流れる電流は $4\:A$ です。
したがって、全体の電流は次の図のように流れています。
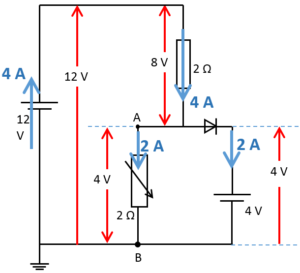
こういった問題は一度やっておくと、実際に出題された場合でも落ち着いて解けるでしょう。
ある程度の経験が必要な問題です。







































コメント