 電磁気
電磁気 トランス 変圧器の原理
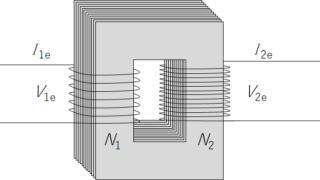
交流電源を採用する理由の一つに、変圧の容易さが挙げられます。今回解説する変圧器を使えば、交流の電圧を簡単に変えることができるのです。このとき、一次コイルの巻き数を $N_1$ 、二次コイルの巻き数を $N_2$ とした場合、一次側の電圧実効値 $V_{1e}$ と2次側の電圧実効値 $V_{2e}$ は次の式に従います。$V_{1e}:V_{2e}=N_1:N_2$
 電磁気
電磁気  電磁気
電磁気  電磁気
電磁気  電磁気
電磁気  電磁気
電磁気  電磁気
電磁気  電磁気
電磁気  電磁気
電磁気  電磁気
電磁気  電磁気
電磁気  電磁気
電磁気  原子物理
原子物理  力学
力学  電磁気
電磁気 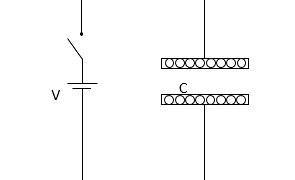 電磁気
電磁気 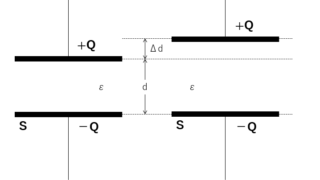 電磁気
電磁気 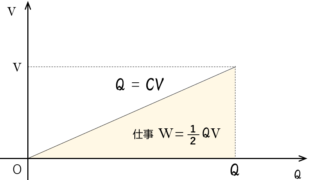 電磁気
電磁気  電磁気
電磁気  波動
波動 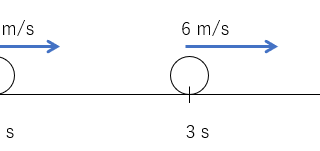 いまさら聞けない
いまさら聞けない