物理のエッセンス・コンデンサー32* の問題です。
まず、アース($0$ V)を決めます。次に電位を仮に $x$ と置いて、電荷保存から問題を解く方法です。
非常にスピーディーに解を求めることができて便利です。
エッセンスの次は良問、そして名問がおすすめです。
Amazon
Amazon
動画
解説(物理のエッセンスコンデンサー32番)
予め充電したコンデンサーを接続した場合に貯まる電気量を求めます。
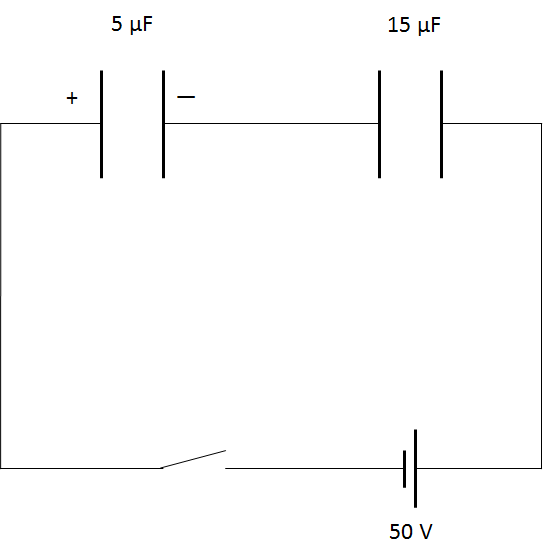
まず $5\:\mathrm{\mu F}$ のコンデンサーを事前に $30$ V で充電しておきます。
そうすると、当然コンデンサーは電荷を持ちます。
\begin{eqnarray}
Q&=&CV\\
&=&5\times30\\
&=&150 \:\mathrm{\mu C}\\
\end{eqnarray}
図にあるように、充電したコンデンサーを直列接続します。
次に、スイッチを閉じます。
そうすると、コンデンサーの電荷は変化するでしょう。
しかし、次の図にあるように赤い点線の内部は電荷が孤立しているのでその電気量総和は $Q_1+Q_2=-150 \:\mathrm{\mu C} $です。
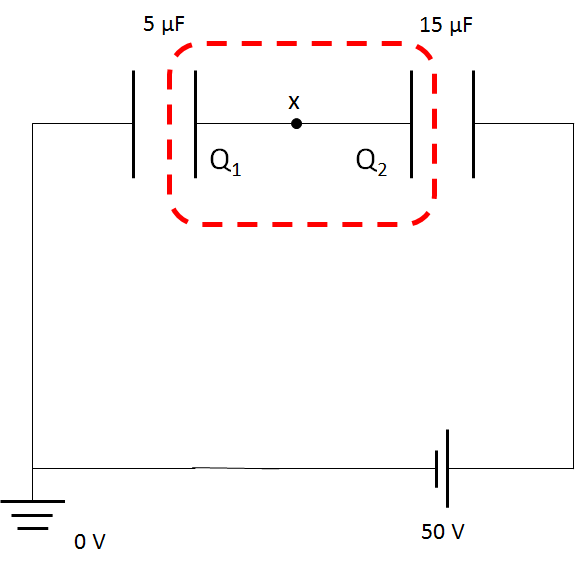
両コンデンサーの間に電位 $x$ を仮定します。
そして、回路の左下側にアースを設置しましょう。
ここが $0$ V です。(どこにアースを仮定してもかまいません!)
そして次に、$Q_1$ と $Q_2$ の電気量を求めます。
これは、$Q=C(V_{自分}-V_{相手})$ とすればOKです。
この考え方は{必殺技による 動画解説エッセンス コンデンサー30* P59}を参考にしてください。
そうすると、電気量総和の式にそれぞれ代入して、
\begin{eqnarray}
Q_1+Q_2&=&5\times(x-0)+15 \times(x-50)\\
&=&150 \:\mathrm{\mu C}\\
\end{eqnarray}
これを解いて、$x=30$ を得ます。
したがって、
\begin{eqnarray}
Q_2&=&15 \:\mathrm{[\mu C]} \times|30-50|\:\mathrm{[V]}\\
&=&300 \:\mathrm{\mu C}\\
\end{eqnarray}
が得られます。
電位を仮定する解き方について(必殺技)
電位を仮定する解き方は非常に便利です。
これは、$Q=C(V_{自分}-V_{相手})$ とすればOKです。
 |
 |
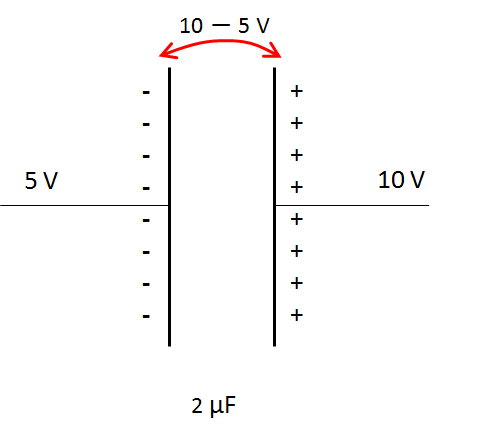
例えば上の左図においてコンデンサーの右極板に貯まる電気量は、$Q=CV$ より、
\begin{eqnarray}
Q&=&C(V_{自分}-V_{相手})\\
&=&2\times (10-5)\\
&=&+10 \:\mathrm{\mu C}\\
\end{eqnarray}
となり、符号もふくめて計算できています。
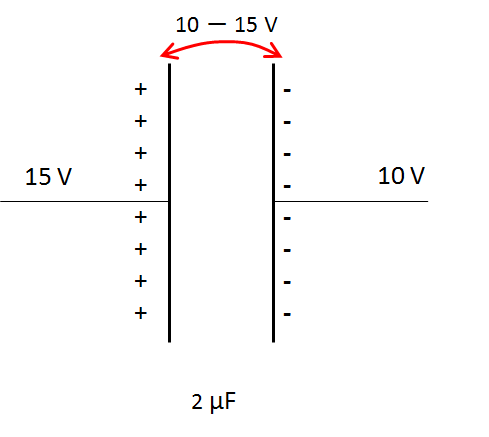
右図においても、右側の極板に貯まる電気量は、
\begin{eqnarray}
Q&=&C(V_{自分}-V_{相手})\\
&=&2\times (10-15)\\
&=&-10 \:\mathrm{\mu C}\\
\end{eqnarray}
となり、正負も含めて成立しています。
$Q=C(V_{自分}-V_{相手})$
ですね。
エッセンスの次は良問、そして名問がおすすめです。
Amazon
Amazon







































コメント