物理のエッセンス 電磁気編 コンデンサー33番です。
この問題は必殺技による解法では電位の仮定箇所を2つ作る必要があります。
したがって、一度はこういう問題を解いて慣れておくべきでしょう。
エッセンスの次は良問、そして名問がおすすめです。
Amazon
Amazon
動画解説
極板上の電気量を求める必殺技
何度か説明しているように極板上の電気量計算は次の式でできます。
$Q=C(V_{自分}-V_{相手})$
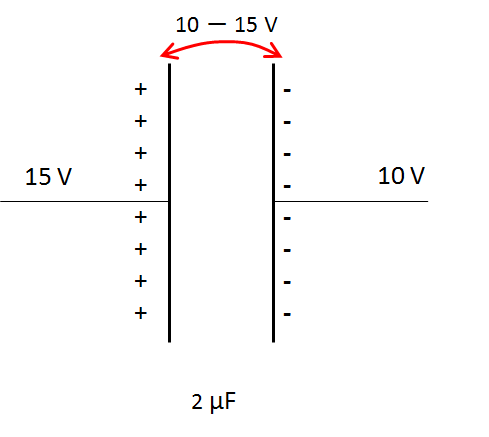
したがって、上の図の例では $10 \:V$ 側に貯まる電気量は
$Q=2\times (10-15)=-10\:\mu C$
次の図の例では $10\: V$ 側に貯まる電気量は
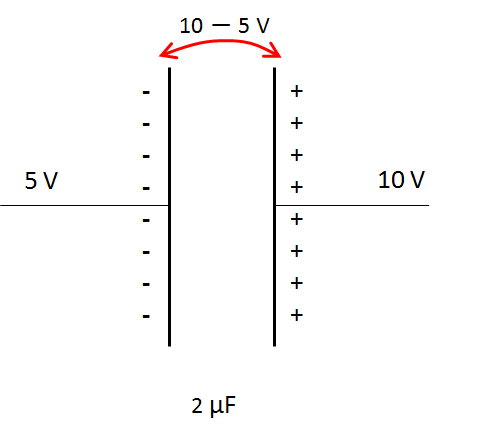
$Q=2\times (10-5)=+10\:\mu C$
となります。
ここで注意してほしいのは、$Q=C(V_{自分}-V_{相手})$ とすることで注目する極板上の電気量をその正負もふくめて計算できることです。
接続前の充電について
それでは問題の解説にうつります。
エッセンス電磁気編コンデンサーの問題 33番を見てください。
まず最初に2つのコンデンサーを充電した上で接続します。
コンデンサーの $C_1$ と $C_2$ は事前に $20\: V$ で充電されているので、それぞれ電気量を $Q_1$ 、$Q_2$ とすれば、
$Q_1=C_1\times V =2\times 20=40\: \mu C$
$Q_2=C_2\times V =1\times 20=20\: \mu C$
となります。
次に、図のようにまず $C_1$ と$C_3$ を接続します。
このとき $C_3$ には電荷はありません。
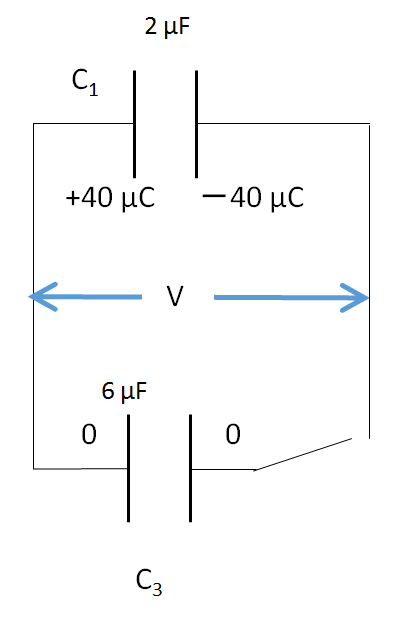
そうするとこれはコンデンサーの並列接続なので電圧は共通です。
$$V=\dfrac{Q}{C}=\dfrac{+40+0}{2+6}=5\: V$$
です。
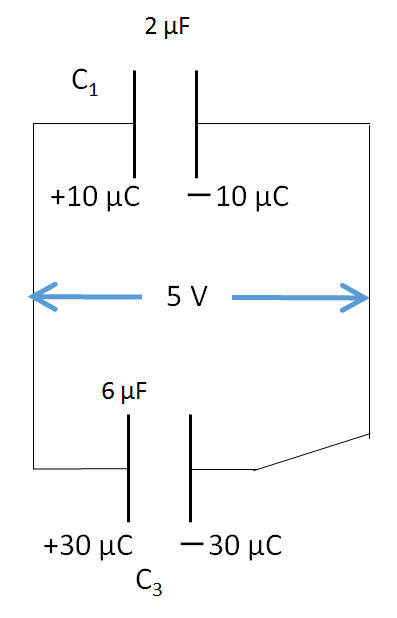
よって、スイッチを入れたあとの各コンデンサーの電気量を考えると、
$$C_1 : Q=2\times 5 =10\: \mu C$$
$$C_3 : Q=6\times 5 =30 \:\mu C$$
となり、図のように電荷が配置されます。
2ヶ所の電位を仮定する
それでは次にもう一つのコンデンサーを接続します。
まだスイッチは入れていません。この時の図の A に貯まる電気量を求めます。
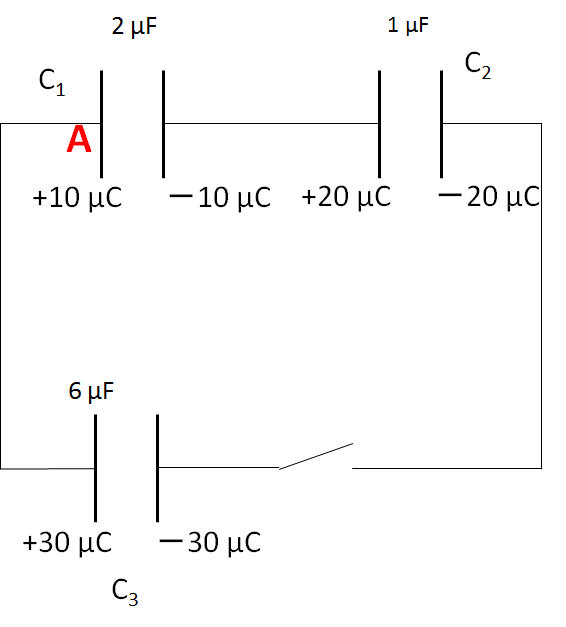
そこで例えば、次の図のように、電気的に孤立している領域を考えます。
この場合は図の赤と青の2つ考えましたが、他の領域でも構いません。
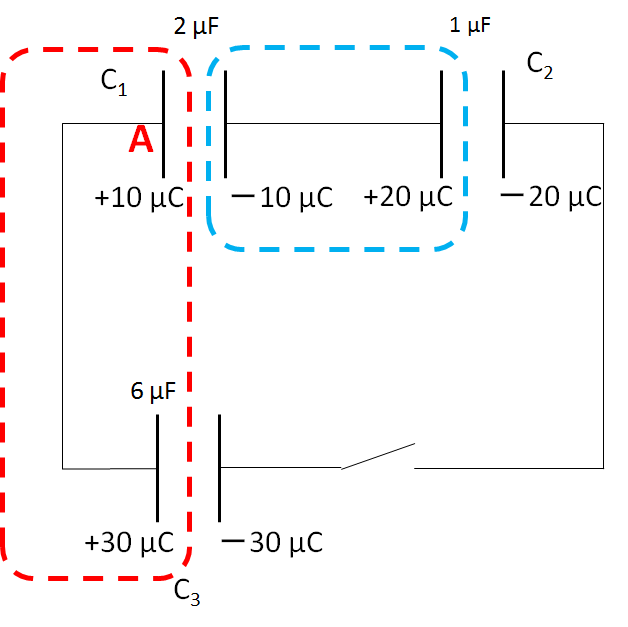
そして次のように適当にアース($0 \:V$)の地点を決めます。
その上で、$x$ と $y$ の電位を設定します。
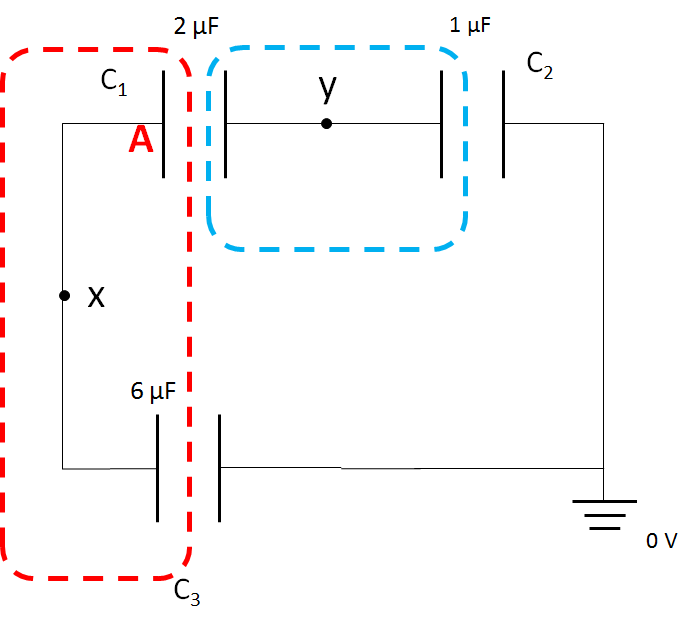
2つの電位を仮定するのがこの問題のミソです。
では赤の範囲からいきましょう。
ここでの総電気量は、 $40+0=40 \:\mu C$ または、$ 10+30=40\: \mu C $ ですね。
よって、
\begin{eqnarray}
Q&=&CV\\
&=&C(V_{自分}-V_{相手})\\
&=&2\times (x-y)+6\times(x-0)\\
&=&40\\
\end{eqnarray}
そして、青の部分については、ここの総電気量は、$-10+20=+10\: \mu C$ です。
したがって
\begin{eqnarray}
Q&=&CV\\
&=&C(V_{自分}-V_{相手})\\
&=&2\times (y-x)+6\times(y-0)\\
&=&10\\
\end{eqnarray}
ですね。
この2つを連立することで、$x=7\:\:\:, \:\:y=8\:\:$ を得ます。
よって図の A に貯まる電気量 $Q$ は
\begin{eqnarray}
Q&=&CV\\
&=&C(V_{自分}-V_{相手})\\
&=&2\times (x-y)\\
&=&2\times (7-8)\\
&=&-2\: \mu C\\
\end{eqnarray}
が得られます。
エッセンスの次は良問、そして名問がおすすめです。
Amazon
Amazon







































コメント