物理のエッセンス解説　電磁気 47番　80ページ

物理のエッセンス解説　電磁気 47番　80ページです。
電圧計と電流計の接続についての問題です。

物理のエッセンス解説　電磁気 47番　80ページ

物理のエッセンスの電磁気編 47番 80ページを参照してください。

Amazon Amazon

動画

電流計と電圧計の接続方法

電流計は回路に直列、電圧計は回路に並列でつなぎます。
　　　なぜかは、この記事の分流器と倍率器についてを見てください。

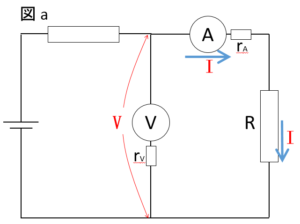
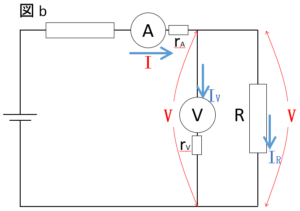
なので、電流計と電圧計は上の図のようにつなぐということになります。

このとき、電流計が示す電流値 $I$ は直列である回路上では同じ。
また、電圧計の示す電圧 $V$ は並列回路においては同じになります。

つまり図aでは、電流計の示す $I$ の電流が抵抗にも流れます。
また図bでは、電圧計の示す $V$  は抵抗の両端にかかる電圧と同じです。

抵抗値の計算

ここで、真の抵抗値を $R$ とします。

そこで、計器から得られた $I$、$V$ から$\dfrac{V}{I}$ を求め、それを $R\;’$ とします。

各図の $R\;’$ を $R$、$r_A$、$R_v$ で示せ。というのが問題になります。

図a

図a から考えていきましょう。

この場合、直列のため、電流 $I$ は抵抗 $R$ でも同じ $I$ です。

また、電圧計の示す $V$ は電流計（内部抵抗 $r_A$）と抵抗 $R$ の両端にかかります。
つまり、電流計と抵抗まとめて、電圧 $V$ かかるというわけです。

したがって電流計と抵抗について考えると、オームの法則 $V=RI$ より、

$V=r_A\times I +R\times I$

$R\;’=\dfrac{V}{I}=r_A+R$

となります。

図b

次に、図b について考えましょう。

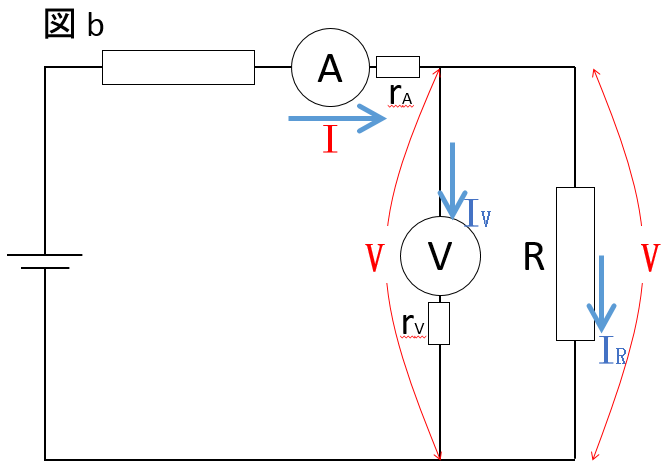
この場合、電流計で計測された $I$ は並列回路において分岐するため、
抵抗 $R$ に $I_R$ 流れ、電圧計に $I_V$ だけ流れるとします。

ここで電流保存の関係から、$I=I_R+I_V$ です。

抵抗 $R$ には $V$ の電圧がかかるため、オームの法則から、$V=R\times I_R$ です。
電圧計についても、両端の電位差が $V$ であるため、$V=r_V\times I_V$ となります。

先程の電流保存の関係の式へ $I_R$ と $I_V$ を代入します。

\begin{eqnarray}
I&=&I_R+I_V\\\\
&=&\dfrac{V}{R}+\dfrac{V}{r_V}\\\\
&=&V\left(\dfrac{1}{R}+\dfrac{1}{r_V}\right)\\ 
\end{eqnarray}

したがって、

\begin{eqnarray}
R\;’&=&\dfrac{V}{I}\\\\
&=&\dfrac{R\times r_V}{R+r_V}\\
\end{eqnarray}

となります。

どのような計器が理想か？

図aの結果から、

のとき、$R\;’=\dfrac{V}{I}=r_A+R$ ですから、$R\;’$ は $r_A \rightarrow 0$ のとき正しい値に近づきます。

また、図bより

$R\;’=\dfrac{R\times r_V}{R+r_V}=\dfrac{R}{\dfrac{R}{r_V}+1}$ なので、$r_V \rightarrow \infty$ のとき正しい値に近づきます。

したがって、電流計の内部抵抗は小さいほど、電圧計の内部抵抗は大きいほど優秀と言えます。