物理のエッセンス 力学45番
滑車を使った問題です。
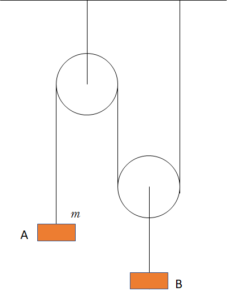
- 図のABがつり合うときの、Bの質量を求める。
- Aが上昇した場合のAの加速度を求める。定滑車をつるしている糸の張力を求める。
解説
1の解説

物体Aと物体Bに着目して、それぞれが受ける外力を図に描き込みます。← 最重要
これがきちんとできれば、ほぼ完成です。
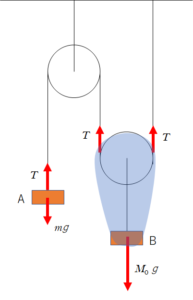
ここでは、簡単のため「図の青い部分」を一体と考えています(滑車の質量は無視できます。)。
動滑車をつかっていることに注意してください。
張力を $T$ として、つり合いの式をたてましょう。
A:$mg=T$
B:$M_0g=2T$
これらより、
$M_0=2m$
2の解説
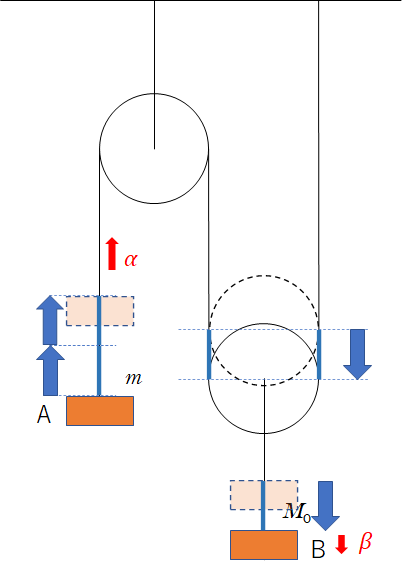
Aが上昇しているため、加速度の方向を、Aは鉛直上向き、Bは鉛直下向きに仮定します。
動滑車を天井に固定している端は、固定されていますから糸を送り出すことがありません。
したがって、Bが図の位置まで下がるためには、下図の 「糸の青い部分×2」 だけAが上昇する必要があります。
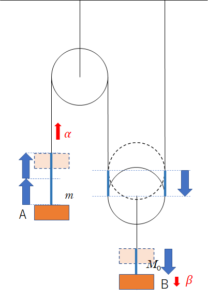

スタートから、A・Bが図の破線で示した位置に上昇/下降するまでの時間は同じです。
また、速度 $v$ は、$v=\dfrac{\Delta x}{\Delta t}$ で示されます。
よって、Aの速さはBの速さの2倍になります。
そして、加速度とは $a=\dfrac{\Delta v}{\Delta t}$ で示されるものです。
つまり、Bが $\Delta t$ の間に、$v$ から $v^\prime$ まで変化したとすると、
$\beta=\dfrac{v^\prime \:-\: v}{\Delta t}$
となります。Aはその瞬間瞬間でBの2倍の速度を持ちますから、
$\alpha=\dfrac{2v^\prime \:-\: 2v}{\Delta t}$
$\:\:\:\:\,=2\times \dfrac{v^\prime \:-\: v}{\Delta t}$
$\alpha=2\beta$
となります。
そのため、Aの加速度もBの加速度の2倍になります。
それでは、図にA、Bそれぞれにはたらく力を描き入れていきましょう。
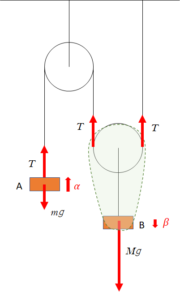
Aの加速度を $\alpha$、Bの加速度を $\beta$ とし、それぞれ進行方向を正とします。
運動方程式は
A:$m\alpha = T \:-\: mg$
B: $M\beta =M\dfrac {\alpha}{2} = Mg \:-\: 2T$
となります。($\alpha=2\beta$ より $\beta=\dfrac{\alpha}{2}$)
これらを解いて、
$\alpha = \dfrac{2(M-2m)g}{4m+M}$
$T=m(a+g)=\dfrac{3mMg}{4m+M}$
を得ます。
また、定滑車を吊り下げている糸の張力の大きさですが、定滑車が受けている力を青色で描いてみます。
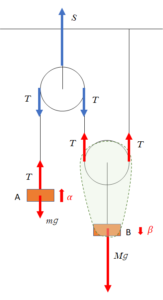
定滑車は静止しているため、糸の張力を $S$ とすると、つり合いの式は次のようになります。(滑車の質量は無視できる)
$S=2T=2\times \dfrac{3mMg}{4m+M}=\dfrac{6mMg}{4m+M}$




































コメント