物理のエッセンス 電磁気 70番
問題概要
エッセンス電磁気の69番の装置で、レールを水平から角度 $\theta$ だけ傾けた状態(図)にして、導体棒PQ( 質量 $m$ )を静かにはなす。磁束密度 $B$ 、重力加速度 $g$ 、レールの間隔 $l$ とする。
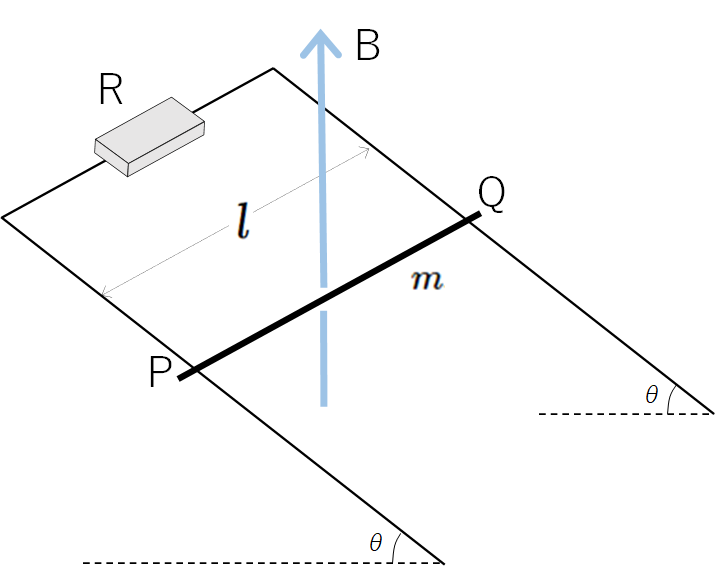
解説
この問題って、終端速度に達するの?? と思う人がいるかもしれません。
しかし、磁場を横切って進む導体棒には誘導起電力が生じ、その結果、回路には電流が流れます。
そうすると、磁場中を運動する電流の流れる導体棒はフレミングの力を受けることになります。
そのとき、フレミングの力により、導体棒は抵抗(ブレーキ)を受けることになります。
フレミングの力の大きさは導体棒に生じる誘導起電力の大きさに比例します。
誘導起電力の大きさは、導体棒の速さに比例する( $V=vBl$ )ため、速さが増すにつれ、導体棒にかかるブレーキは大きくなっていきます。
そして、あるところで導体棒にはたらく全ての力がつり合います。
慣性の法則から、「物体に力がはたらかない、あるいは物体にはたらく力がつり合っている場合、物体は静止または、等速直線運動を続ける」を思い出すと、この導体棒は力がつり合って以降、等速直線運動をすることになります。つまり、このときの速さが終端速度になるというわけです。
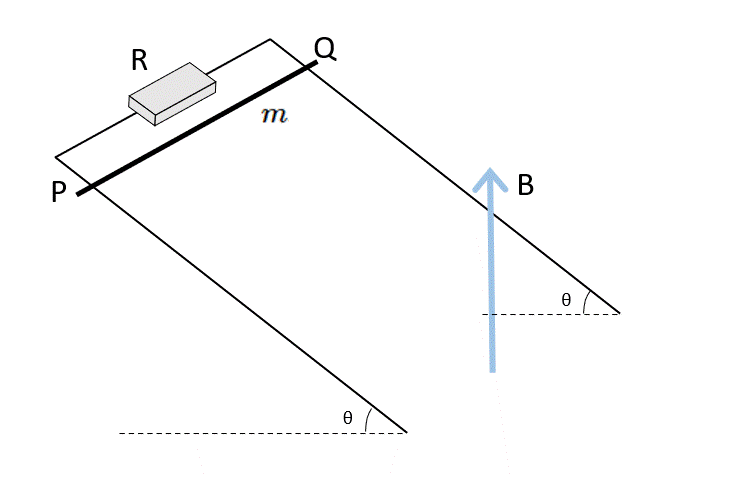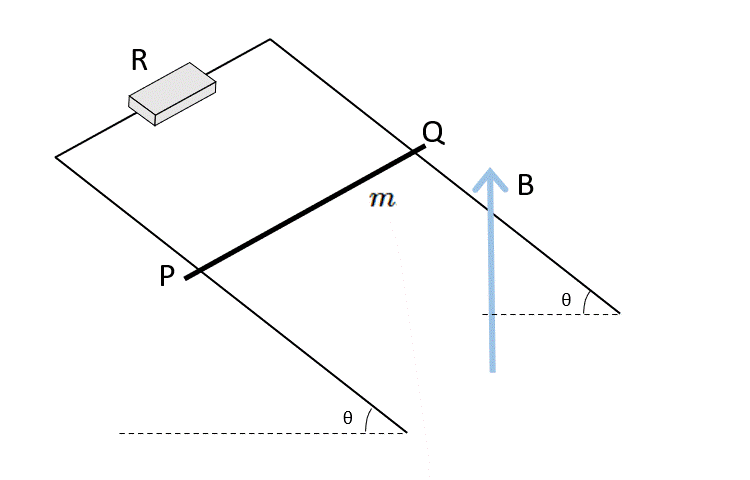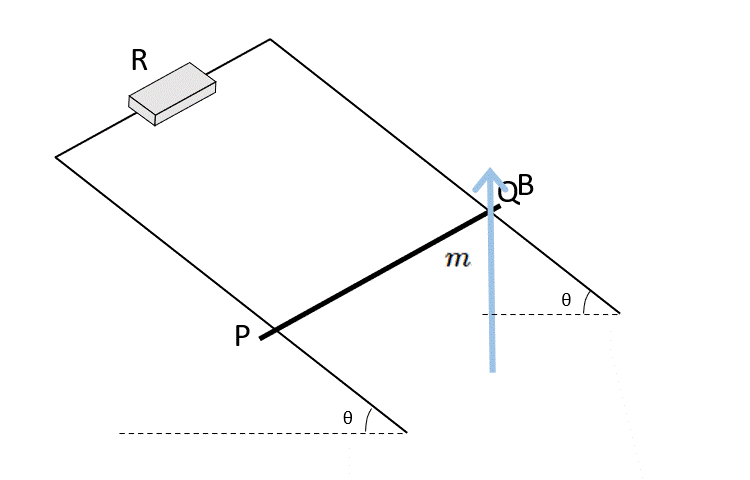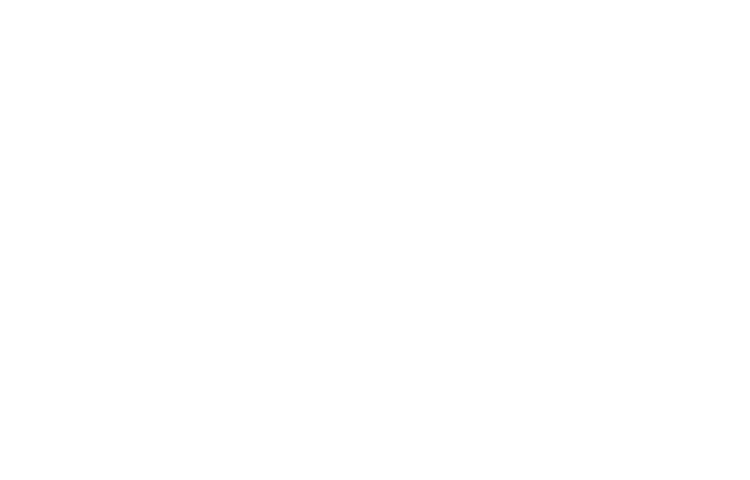
終端速度になった状態では、導体棒の運動エネルギーは増加しませんが、位置エネルギーを失います。
エネルギー保存則により、位置エネルギーは電気エネルギーへと変換され、さらに抵抗で熱エネルギーとなって散逸します。
導体棒の終端速度 $v_1$ を求める
レールに沿って滑る導体棒の速さを $v$ としたとき、磁場の向きに対して垂直な方向の速さを求める必要があります。
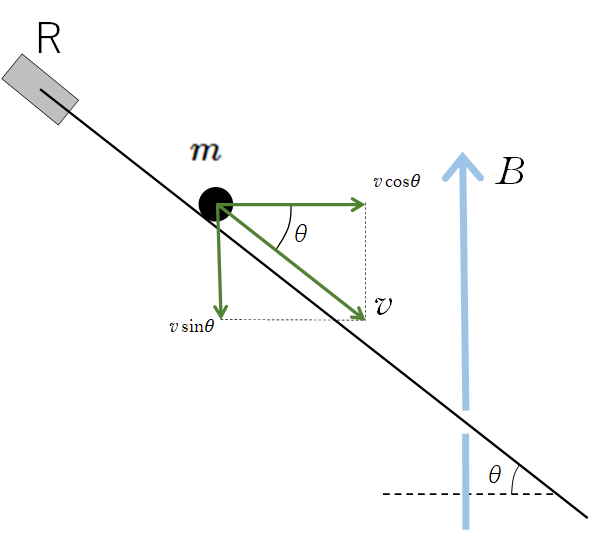
図より、 $B$ に垂直な方向(水平方向)の速さは $v\cos\theta$ となるため、導体棒に生じる誘導起電力の大きさ $V$ は、 $V=vBl$ より

起電力 ( $V$ ) はバーベル ( $vBl$ ) と覚えましょう。
$V=(v\cos\theta)Bl$
回路の抵抗は $R$ ですから、回路に流れる電流の大きさ $I$ は、オームの法則より、
$I=\dfrac{V}{R}=\dfrac{(v\cos\theta)Bl}{R}$
よって、導体棒にはたらくフレミングの力 $F$ は、
$F=IBl=\dfrac{(v\cos\theta)Bl}{R} Bl =\dfrac{(v\cos\theta)B^2l^2}{R}\:\cdots\cdots\:(1) $
で、磁場に垂直な方向、すなわち水平方向になります。

$F=IBl$
$BIl$(ビール)は力 ($F$)と覚えましょう。
今、終端速度 $v_1$ に達したとすると、導体棒にはたらく力はつり合っているはずですから、力の図は次のようになります。
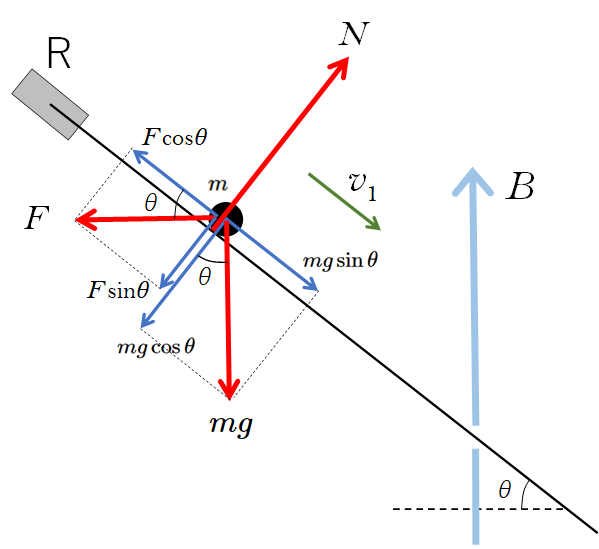
よって、導体棒に平行な方向のつり合いを考えれば、
$F\cos\theta=mg\sin\theta \:\cdots\cdots\:(2)$
ここで、式 $(1)$ を $v \rightarrow v_1$ と書き換え
$F=\dfrac{(v_1\cos\theta)B^2l^2}{R}$
として、$(2)$ へ代入します。
$F\cos\theta=mg\sin\theta$
$\left \{ \dfrac{(v_1\cos\theta)B^2l^2}{R} \right \} \cos\theta=mg\sin\theta$
よって、
$ \dfrac{v_1 B^2l^2 \cos^2\theta}{R} =mg\sin\theta$
より、
$v_1 = \dfrac{mgR\sin\theta}{(Bl\cos\theta)^2}$
途中で導体棒の速さ $v$ のときの加速度 $a$ を求める
導体棒の速さを $v$ 、斜面下方向を正として、運動方程式を立てると図より、
$ma = mg\sin\theta -F\cos\theta$
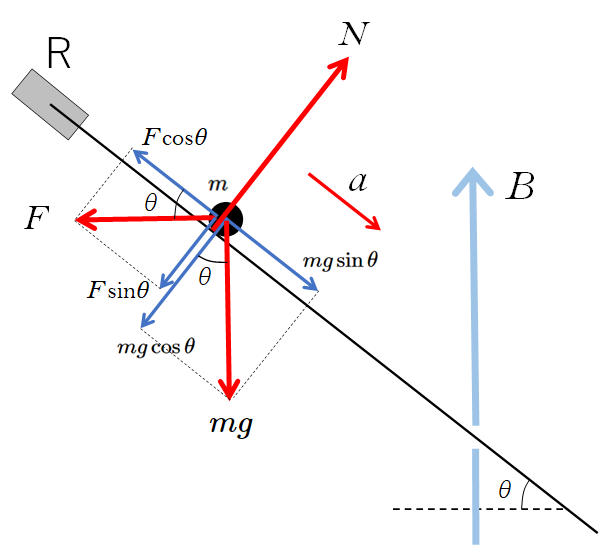
ここで、$(1)$ より、 $F=\dfrac{(v\cos\theta)B^2l^2}{R}$ だから、
$ma = mg\sin\theta -F\cos\theta$
$ma = mg\sin\theta -\left \{ \dfrac{(v\cos\theta)B^2l^2}{R} \right \} \cos\theta$
$a = g\sin\theta \:-\: \dfrac{v(Bl\cos\theta)^2}{mR} $
終端速度について
問題 2 の運動方程式より、
$ma = mg\sin\theta -\left \{ \dfrac{(v\cos\theta)B^2l^2}{R} \right \} \cos\theta$
$~~~~~~= mg\sin\theta -\left \{ \dfrac{(Bl\cos\theta)^2}{R} \right \}v$
において、
$\left \{ \dfrac{(Bl\cos\theta)^2}{R} \right \}=k$ $k$:(定数)
とし、 $g\sin\theta = g’$ とおくと、
$ma = mg’ \:-\: kv$
$a=g’ \:-\: \dfrac{k}{m}v$
これは、空気抵抗 $kv$ を受けて落下する物体の終端速度に関する式と同じ形です。
その速度・加速度と時間のグラフは次のようになります。
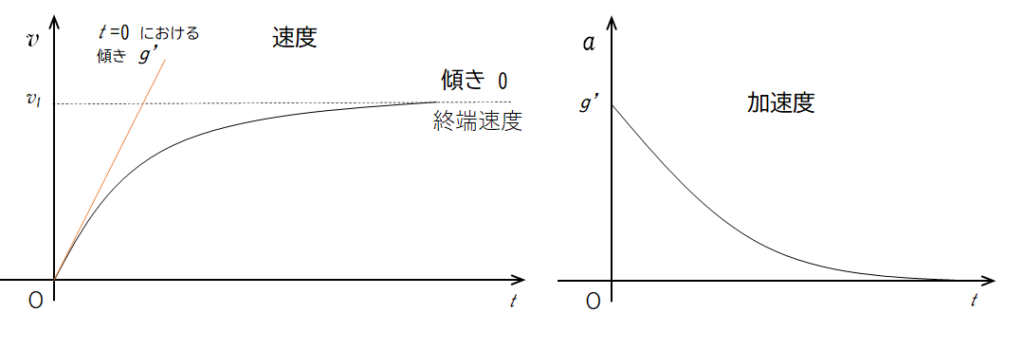
したがって、終端速度 $v_1$ は、$a=0$ の場合だから
$ma = mg’ \:-\: kv$
より、
$0= mg’ \:-\: kv_1$
であるから、
$v_1=\dfrac{mg’}{k}$
です。よって、これに、
$k=\left \{ \dfrac{(Bl\cos\theta)^2}{R} \right \}$
$g’=g\sin\theta$
を代入して、
$v_1=\dfrac{mg’}{k}$
$~~~~=\dfrac{mg\sin\theta}{\left \{ \dfrac{(Bl\cos\theta)^2}{R} \right \}}$
より、
$v_1 = \dfrac{mgR\sin\theta}{(Bl\cos\theta)^2}$
となります。
終端速度については以下を参考にしてください。






































コメント