物理のエッセンス　電磁気72番

物理のエッセンス　電磁気72番 

解説

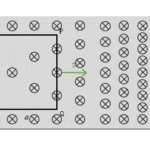
半径 $a$ の円形領域を考える。
その領域で、画面の背後から表へ向けて磁束密度が単位時間当たり $b$ で増加している。

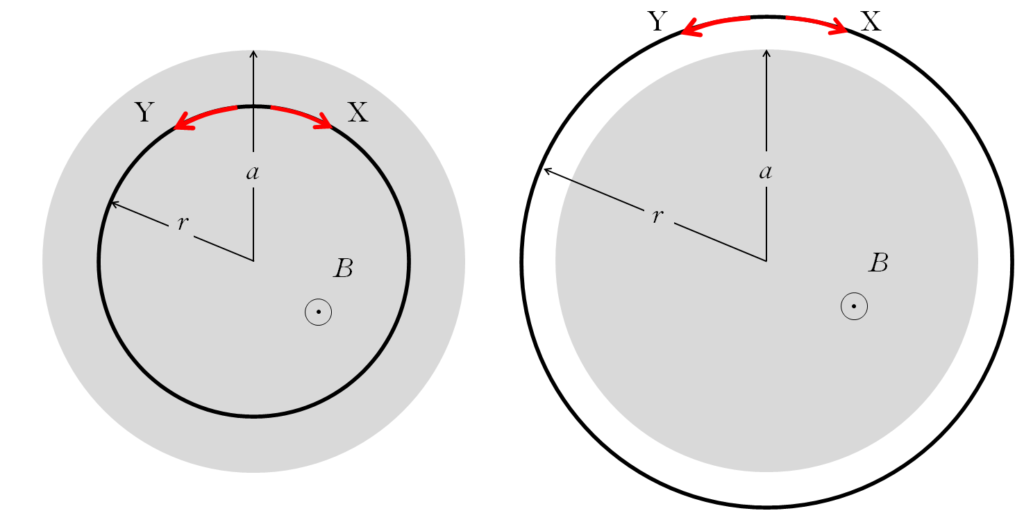
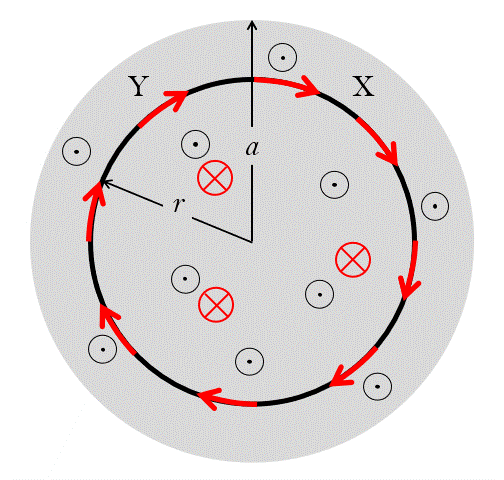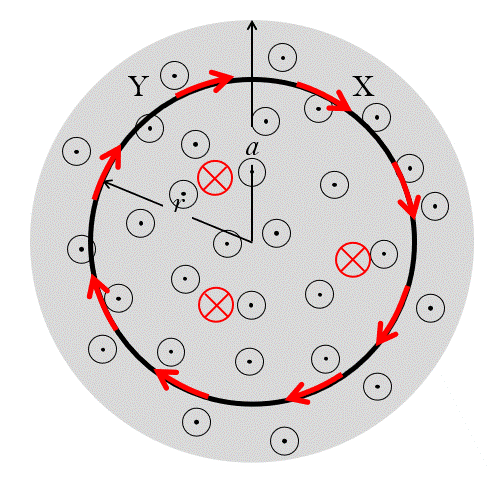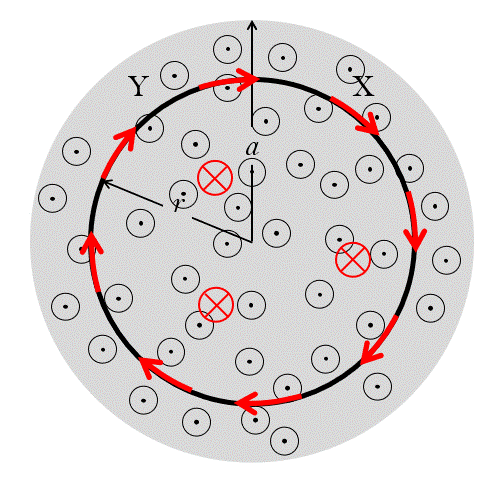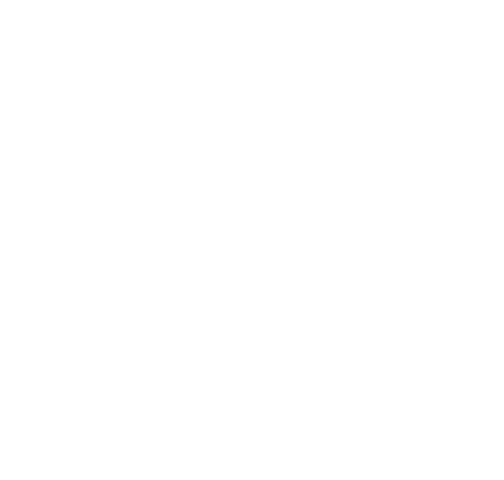
領域内にある半径 $r$ の一巻コイルに生じる誘導起電力 $V$ の向き

レンツの法則から、コイルには画面の表から背後へ向かう磁束が増加するように誘導起電力が生じ、誘導電流が流れるはずです。

したがって右手の法則から、$X$ 方向に電流が流れます。

誘導起電力の大きさは、単位時間にどれだけ磁束密度が増減するか･･･で決まります。

したがって、磁束密度の増減の速度が一定であれば、

磁束がたくさんになってきても同じ大きさの誘導起電力が生じ、

同じ大きさの誘導電流が流れます。

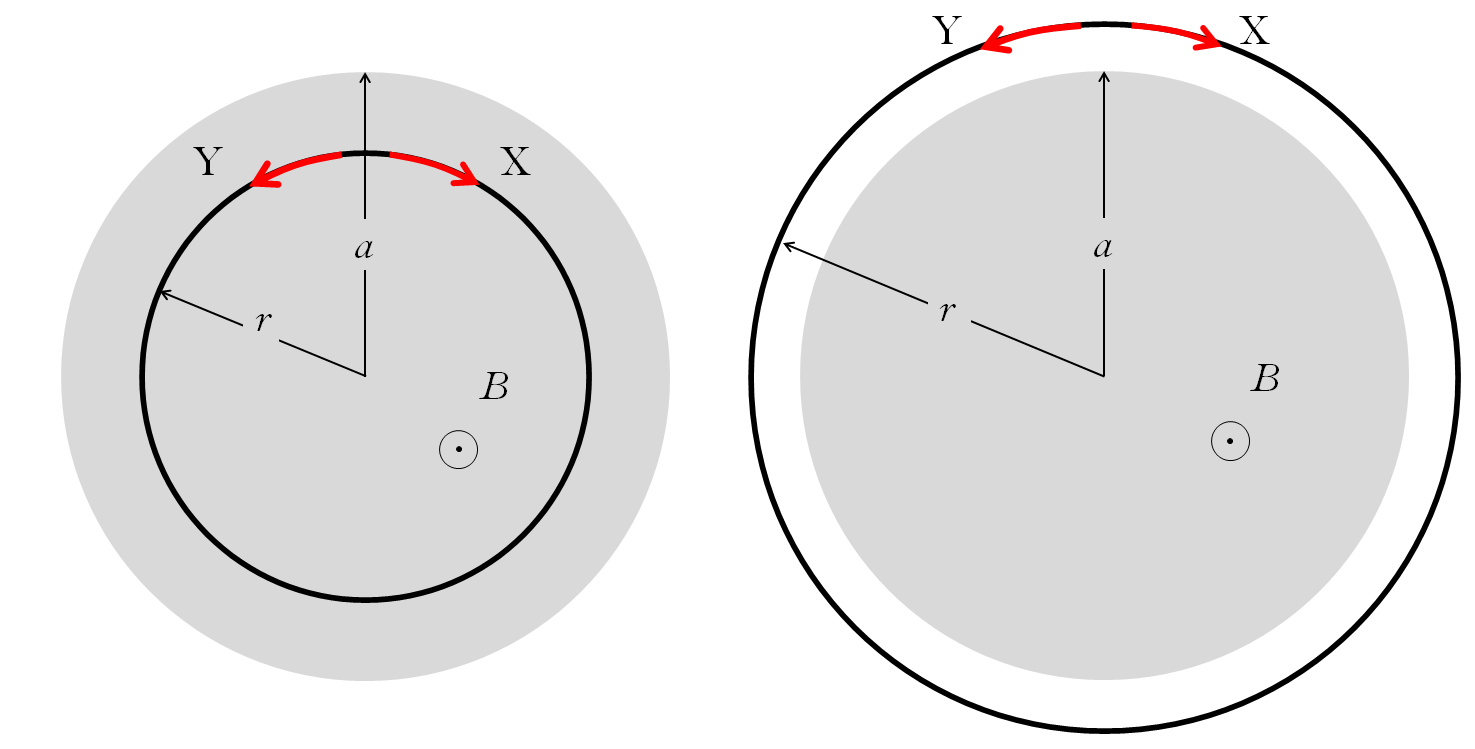
コイル半径 $r \leqq a$  のときの $V$ の大きさ

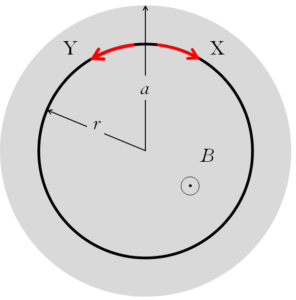
磁束密度を $B(t)$ とすると、磁束密度が単位時間当たり $b$ で増加しているため、時間を $t$ として、

$ B(t)=B(0) + bt $

と示すことができます。

ファラデー電磁誘導の法則から

$V=-N\dfrac{\Delta \Phi}{\Delta t}$　と　$\Phi = BS $

において、 $\Phi$ は時間 $t$ の関数だから $\Phi(t)$ と表記することにします。
$S=\pi r^2$　だから、

$\Phi(t) =\pi r^2 [ B(0) + bt ]$

$V$ の大きさを考えて、

$V=N\dfrac{\Delta \Phi(t)}{\Delta t}$　　( $N=1$ ) 

$~~~=\dfrac{ \Phi(t+\Delta t)-\Phi(t)}{\Delta t}$

$~~~=\dfrac{ \pi r^2 [ B(0) + b \times (t+\Delta t) ] \:-\:\pi r^2 [ B(0) + bt ]}{\Delta t}$

$~~~=\pi r^2  \dfrac{b \Delta t }{\Delta t}$

$~~~=\pi r^2b $

$V=N\dfrac{\mathrm{d} \Phi(t)}{\mathrm{d} t}$　　( $N=1$ )

と微分形で考えれば、

$V=\dfrac{\mathrm{d} \left \{\pi r^2 [ B(0) + bt ] \right \}}{\mathrm{d} t}$

$V=\pi r^2b$

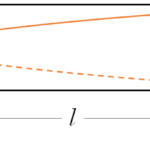
コイル半径 $r > a $  のときの$V$ の大きさ

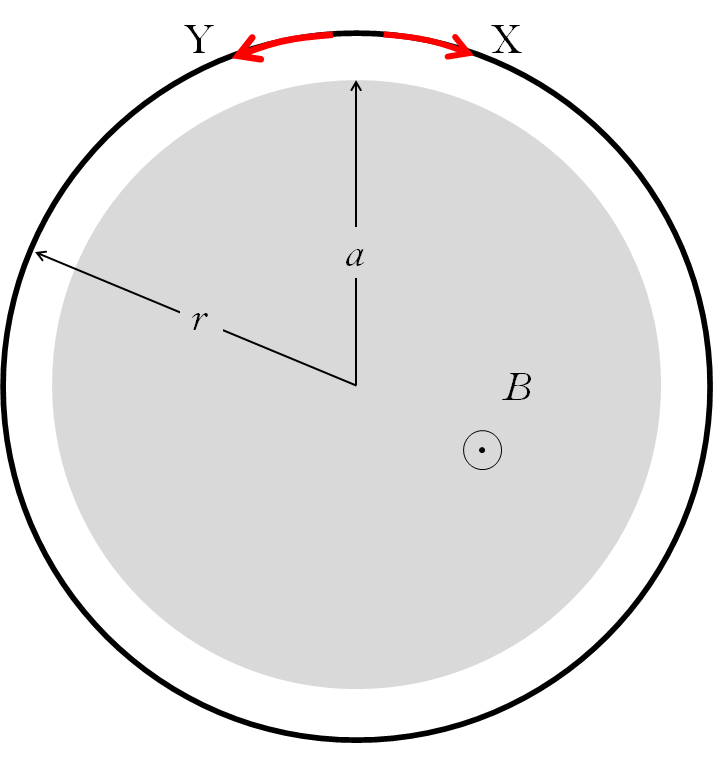
コイル半径 $r$ が領域半径 $a$ よりも大きいときは、コイルを貫く磁束線の面積は $\pi a^2$ です。

したがって、 $r \rightarrow a$　と書き換えて、

$V=\pi a^2b$