動画解説エッセンス　コンデンサー EX2 64ページ

物理のエッセンスの電磁気編コンデンサーの例題 EX2 について解説します。
エネルギーの原理を使って解いていきます。

動画解説

物理のエッセンスの電磁気編 P64 の EX の問題を参照してください。
動画解説を行っています。 

解説

物理のエッセンス・コンデンサーの例題 EX2 P64 です。

こういった回路の場合気をつけることは電池のスイッチを入れっぱなしにしていることです。
問題によってはスイッチを入れたり切ったりしますので注意が必要です。

極板間に金属板を入れる時の容量

スイッチを入れっぱなしにしている場合はコンデンサーの極板間電圧は $V$ で変わりません（極板上の電気量は変化します）。電池により保証されているのです。注意
 スイッチを切っている場合、電圧は変化しますが電気量は変化しません。

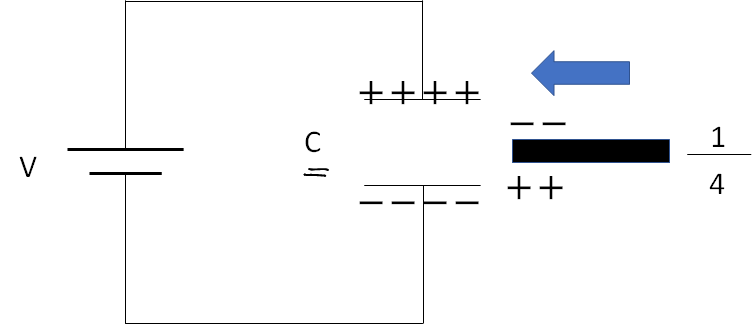
コンデンサーの内部に金属板を挿入するのですが、その際のコンデンサーの容量の変化については以下の記事を参考にしてください。

コンデンサー内への金属板・誘電体挿入について

コンデンサー内に薄い金属板や誘電体を挿入する場合の容量はどうなるでしょうか？ この場合の容量は、挿入した金属板や誘電体はスライドさせても同じです。 なぜでしょうか？一緒に考えていきましょう。 誘電体挿入と電位・電場とグラフについてはこちらを

kokolainen.com

コンデンサーの電気容量は、金属版をコンデンサー内のどの位置に移動させても同じです。なので金属板をコンデンサー内の一番下か一番上に寄せてしまいましょう。

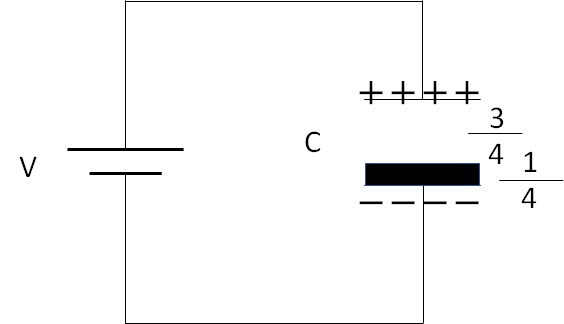
したがって、もとのコンデンサーの容量が $C$ ですから、

$C=\epsilon \dfrac{S}{d}$
金属板を入れた後のコンデンサー容量 $C\:’$ は、
$C\:’=\epsilon \dfrac{S}{\frac{3}{4}d}=\dfrac{4}{3}C$

となります。

外力の仕事 $W_1$ とは

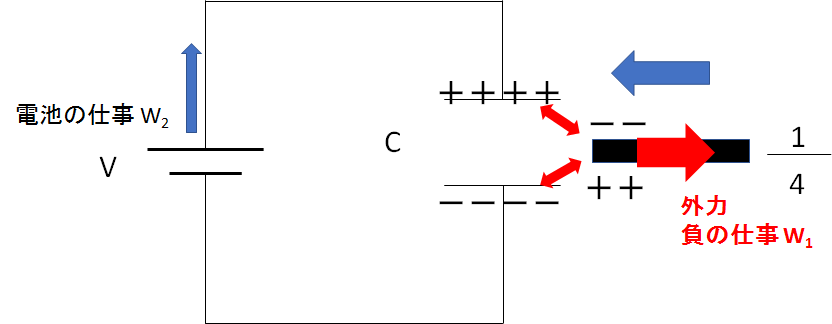
金属板をゆっくりと挿入するためには、外力を図のように金属板の挿入方向と反対向きに働かせなければなりません。
なぜなら静電誘導によって生じた電荷が引き合うため、金属板が引き込まれるからです。
すなわち、それに対抗する力が金属板の挿入方向と反対方向に必要です。
よって、この外力のする仕事 $W_1$ は負の仕事になります。

エネルギーの原理を考える

さて、本題に入りましょう。
実はこのときの仕事は外力によるものだけではありません。
回路に電池が繋がれているため、コンデンサーの電気量が増減して電池が頑張って仕事をします。
その仕事は次の式で表されます。

$W=\Delta q V$

では、エネルギーの原理を使って考えましょう。
その際、最初のエネルギー ($E_0$) ＋ 仕事 ($W$) ＝ 後のエネルギー ($E$)  として考えます。

つまり、$W_1$ を外力の仕事、$W_2$ を電池のする仕事とすると、
$E_0+\{W_1+W_2\}=E$

です。

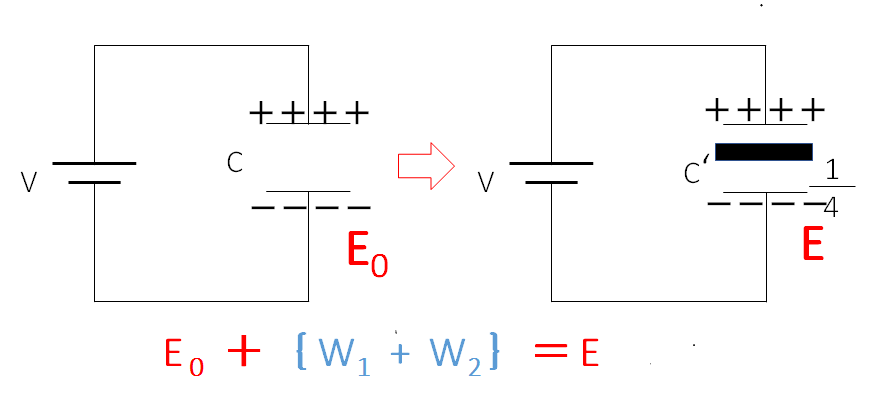
このとき、コンデンサーのエネルギーは、$E=\dfrac{1}{2}CV^2$ ですね。
よって $C\:’=\dfrac{4}{3}C$ より、
$E_0=\dfrac{1}{2}CV^2$
$E=\dfrac{1}{2}C\:’V^2=\dfrac{1}{2}(\dfrac{4}{3}C)V^2$

です。また、金属板挿入前のコンデンサーの電気量を $Q$、後を $Q’$ とすると、電気量の変化 $\Delta q=Q’-Q$ 、$Q=CV$、$Q’=C\:’V=\dfrac{4}{3}CV$ なので、
$\Delta q=Q’-Q=\dfrac{4}{3}CV-CV=\dfrac{1}{3}CV$

ゆえに、$W_2=\Delta qV=\dfrac{1}{3}CV^2$

それぞれを $E_0+\{W_1+W_2\}=E$ へ代入すると、

$\dfrac{1}{2}CV^2+\{W_1+\dfrac{1}{3}CV^2\}=\dfrac{1}{2}(\dfrac{4}{3}C)V^2$

より、$W_1=-\dfrac{1}{6}CV^2$

となります。
このとき $-$ がついているのは負の仕事を表しています。

この問題では「電池のする仕事」を忘れがちなので気をつけましょう！