物理のエッセンス解説　電磁気 53番 54番　87ページ

コンデンサーを含む回路でスイッチをオン/オフする・・よくある問題ですが、苦手にしている人も多いのではないでしょうか？
今回は、物理のエッセンスの青、電磁気編の87ページの 53番と54番について解説します。

もっと難しい問題もありますが、基本はコレです。
まずは基礎をしっかりと理解することを心がけましょう。

物理のエッセンス解説　電磁気 53番 54番　87ページ

物理のエッセンスの熱・電磁気編（通称青）の87ページを開けて下さい。

エッセンスの次は良問の風・そして名問の森１名問の森２がオススメ

解説

物理のエッセンスの熱・電磁気編（通称青）の87ページを開けて下さい。

53番

まずは53番からです。

53番動画解説

---

まず一つ目
 
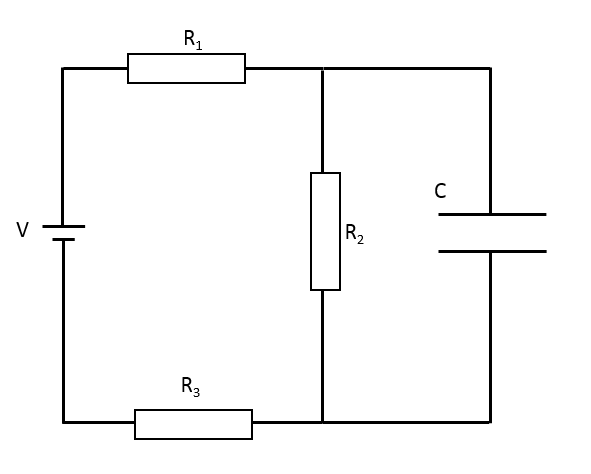
このときのコンデンサーの電気量を計算します。

このとき、定常状態（十分時間がたったとき）では、コンデンサー C と抵抗 $R_2$ にかかる電圧は同じです。

ゆえに、$R_2$ の抵抗にかかる電圧を計算すれば、$Q=CV$ を用いてコンデンサーの電気量を計算できます。

抵抗 $R_1$、$R_2$、$R_3$ に掛かる電圧をそれぞれ、 $V_1$、$V_2$、$V_3$ とします(図）。

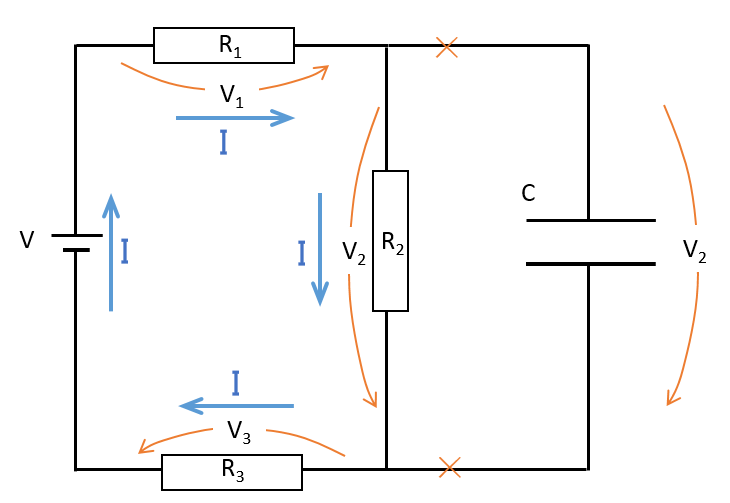
このとき、定常状態であればコンデンサーの方には電流は流れません。
したがって、各抵抗には同じ電流が流れることになります。 
その電流を $I$ として電圧比をとると、オームの法則から次の式が成り立ちます。

$V_1:V_2:V_3=R_1I:R_2I:R_3I=R_1:R_2:R_3$

したがって、

$V_2=\dfrac{R_2}{R_1+R_2+R_3}V$

よって、$Q=CV$ より、コンデンサーの電気量は

$Q=CV_2=\dfrac{R_2}{R_1+R_2+R_3}CV$

となります。

---

それでは続いて二つ目です。

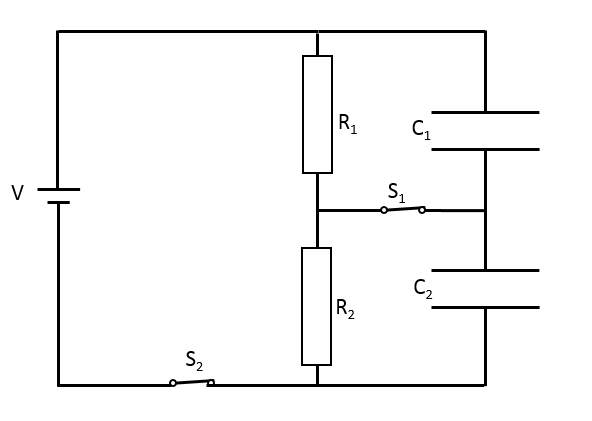
このときの各コンデンサーに貯まる電気量を計算します。
このとき、スイッチ $S_1$ が閉じているため、定常状態（十分時間がたった状態）においては、
$R_1$ 抵抗と $C_1$ コンデンサー、および$R_2$ 抵抗と $C_2$ コンデンサーにかかる電圧はそれぞれ同じになります。

このとき、定常状態なのでコンデンサー側には電流は流れていません。

ゆえに、$R_1$ と $R_2$ の各抵抗に掛かる電圧を計算すればあとは、$Q=CV$ を用いてそれぞれのコンデンサーの電気量を計算できます。

抵抗 $R_1$、$R_2$ に掛かる電圧をそれぞれ、 $V_1$、$V_2$ とします(図）。

図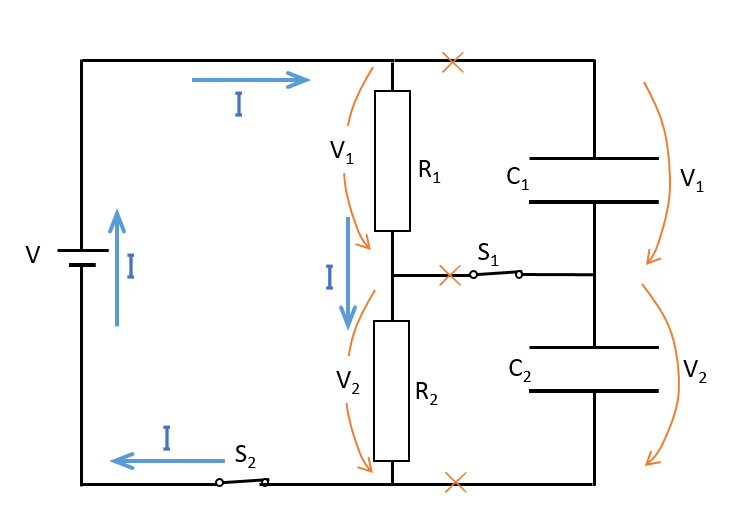

このときも、各抵抗には同じ電流が流れることになります。 
その電流を $I$ とすると、オームの法則から次の式が成り立ちます。

$V_1:V_2=R_1I:R_2I=R_1:R_2$

したがって、

$V_1=\dfrac{R_1}{R_1+R_2}V$

$V_2=\dfrac{R_2}{R_1+R_2}V$

よって、$Q=CV$ より、コンデンサー $C_1$,$C_2$ の電気量をそれぞれ $Q_1$,$Q_2$ とすると、

$Q_1=C_1V_1=\dfrac{R_1}{R_1+R_2}C_1V$

$Q_2=C_2V_2=\dfrac{R_2}{R_1+R_2}C_2V$

となります。

54番　必殺技による解法

つづいて54番です。
今回はこちらが本命です。

54番動画解説

---

53番の問題で $C_1, C_2$ 各コンデンサーに 溜まっている電気量はそれぞれ $Q_1$, $Q_2$ と計算できました。
続いてその状態のまま、スイッチを $S_1$ $\rightarrow$ $S_2$ の順番で切っていきます。

そして、$C_1$ に貯まる電気量を求めます。

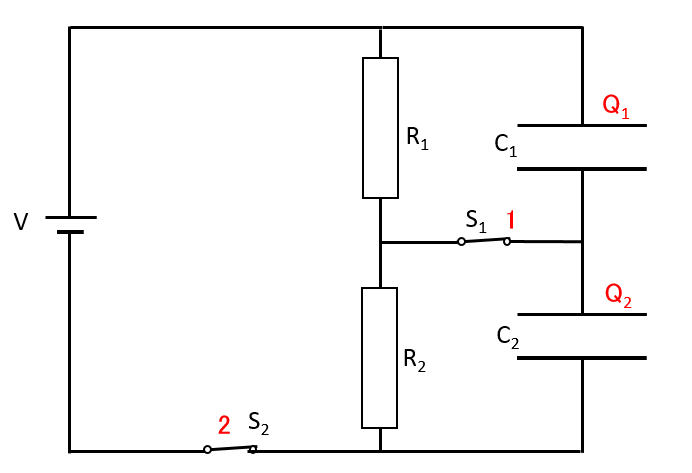
まずスイッチ $S_1$ を最初に切った直後ですが、特になにも起こりません。
なぜかというと、スイッチ $S_1$ があるコンデンサーと抵抗を結ぶ導線には定常状態で電流が流れていませんでした。
そのため、スイッチ $S_1$ を切ったところで状態は変わらないのです。

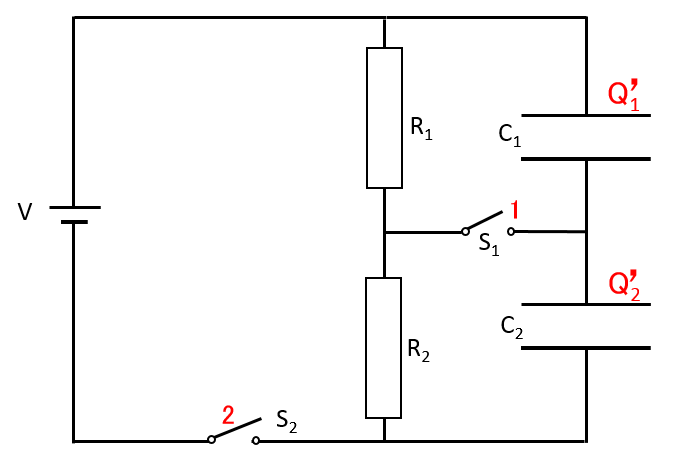
つづいて、スイッチ $S_2$ を切ると電源電圧が消失するため電荷が移動します。
そこで、その状態でのコンデンサー $C_1$,$C_2$ の新しい電気量をそれぞれ $Q\, ^\prime_1$,$Q\,^\prime _2$ とします。

次の図において、青の点線内部は電気的に孤立しているため、スイッチ $S_2$ を切る前と後と比べても総電気量は変化していません。このことを利用します。

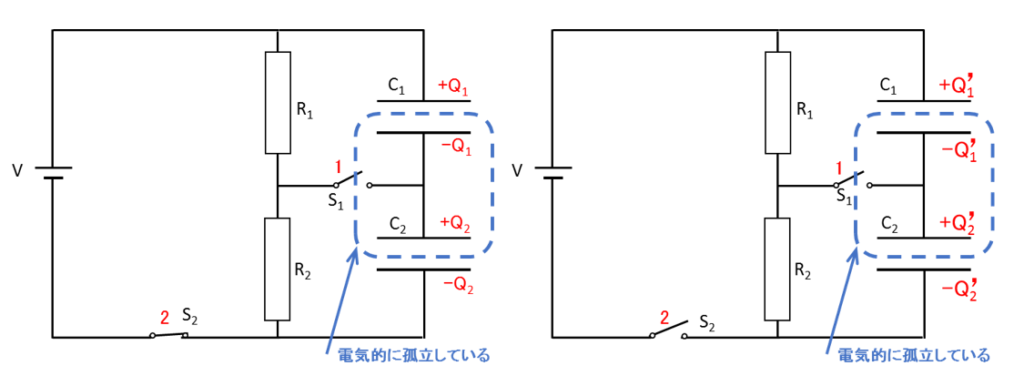
スイッチを切っても総電気量は同じですから次の式が成り立ちます。

$-Q_1+Q_2=-Q\,^\prime_1+Q\, ^\prime_2$

それでは上の2番めの図を見やすいように回転させましょう。（別にしなくても構いませんが）

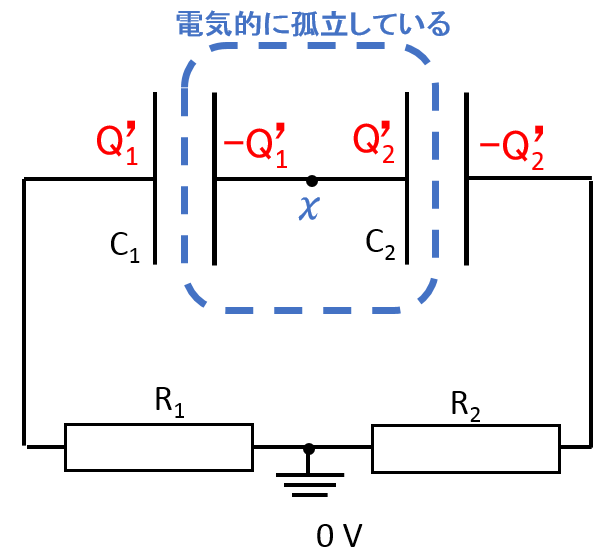
ここで図のように電位の基準点（アース）を考えます。別にアースでなくてもよい（コンデンサーの電圧がわかれば良い）のですが、基準を $0 V$ として、わかりやすくするためアースを入れました。

次に図の電位を $x$ と仮定します。
いまこの状態は定常状態なので回路に電流は流れていません。
したがって、抵抗による電圧降下は 0 で抵抗は導線と考えて差し支えありません。

ということは、コンデンサーの $x$ の反対側の極板の電位は $C_1,\:\:C_2$ ともに $0 V$ です。 

$Q=CV$ より、

$-Q_1+Q_2=-Q\,^\prime_1+Q\, ^\prime_2$
$~~~~~~~~~~~~~=C_1(x-0)+C_2(x-0)$

$x=\dfrac{-Q_1+Q_2}{C_1+C_2}$

 

 

よって、$C_1$ の内側（$x$ 側）に貯まる電気量は $x$ を代入して、

\begin{eqnarray}
Q&=&C_1(x-0)\\
&=&C_1\times x\\\\
&=&C_1\dfrac{-Q_1+Q_2}{C_1+C_2}\\\\
&=&\dfrac{C_1}{C_1+C_2}\times \dfrac{V}{R_1+R_2}(-C_1R_1+C_2R_2)
\end{eqnarray}

となります。
問題は $C_1$ に貯まる電気量を問うていますから、絶対値をつけて

$Q=\dfrac{C_1V}{(C_1+C_2)(R_1+R_2)}|C_1R_1-C_2R_2|$

とします。

54番　並列を使用した解法

結局一緒のことなのですが、並列ということを考えて解いてみましょう。

回路は定常状態にあるので、抵抗での電圧降下はありません。
したがって、図のような並列回路が接続されたのと意味としては同じです。
このとき、コンデンサーの合成容量は $C_1+C_2$ とできますね。

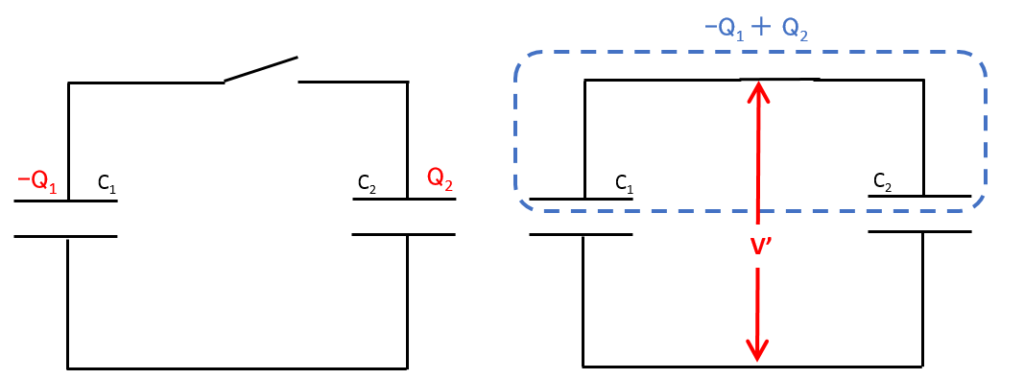
また、青の点線の枠内の総電気量は $-Q_1+Q_2$ です。
平行なので、両コンデンサーにかかる電圧は等しく、それを $V’$ とおきます。
となると、$Q=CV$ より、

$V’=\dfrac{-Q_1+Q_2}{C_1+C_2}$

よって、$C_1$ に貯まる電気量は

$Q=C_1V’=C_1\dfrac{-Q_1+Q_2}{C_1+C_2}$

となります。
答えは、これに $-Q_1+Q_2=(-C_1R_1+C_2R_2)\dfrac{V}{R_1+R_2}$ を代入して得られます。
問題は $C_1$ に貯まる電気量を問うていますから、絶対値をつけて

$Q=\dfrac{C_1V}{(C_1+C_2)(R_1+R_2)}|C_1R_1-C_2R_2|$

とします。

Ｚ会Asteria　まずは無料でお試しください