【動画追加】物理のエッセンス解説　電磁誘導 68番 P101

電磁誘導の問題です。
電磁誘導 68番 P101、この問題が電磁誘導の基礎となると思います。
レンツの法則・右手の法則・フレミング左手の法則・ファラデー電磁誘導の法則などを確認しておきましょう。

物理のエッセンス解説　電磁誘導 68番 P101

物理のエッセンス　電磁誘導 68番 P101　を参照してください。

問題　68番

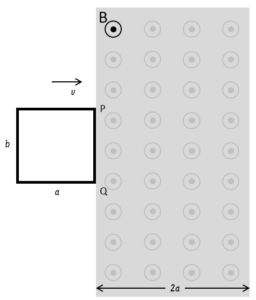
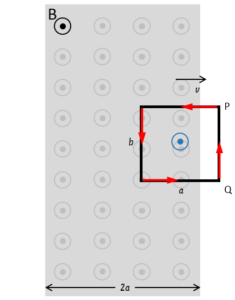
図のような簡単なコイルを等速で磁束密度Bの中を通過させます。
コイルには適当な外力を加えることで、一定の速さ $v$ で通過させるものとします。
また、コイル全体の電気抵抗を $R$  とします。

(1)電流の時間的な変化のグラフを描く

(2)コイルを引くための外力のグラフを描く

図の辺PQが磁場に達した時を時刻 $t=0$ とします。

解説

動画

 

まず、大事なことはファラデー電磁誘導の法則の理解です。
ファラデー電磁誘導の法則とは次の式で示されるもので、

$V=-N\dfrac{\Delta\Phi}{\Delta t}$

コイルを貫く、単位時間あたりの磁束 $\Phi$ の変化分が誘導起電力、というものでした。
　　　　このときの $N$ はコイルの巻数を、マイナス $-$ はレンツの規則を示しています。

したがって、どのような強力な磁場が存在するところでも、その磁束が変化しなければ、誘導起電力は $0$ です。

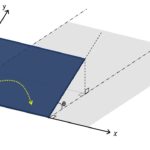
なので、コイルが完全に一様な磁場中に埋もれているとき・・・例えば次図のようなときは、コイルが動いていても誘導起電力は $0$ なのです。

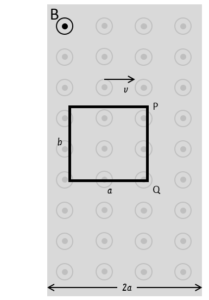
コイルに誘導起電力が生じるのは、次の図にあるようなコイルが磁場に入りかけか、出かけのときに限られます。このときコイルを貫く磁束に変化があらわれます。

では、ことのきコイルに生じる誘導起電力の大きさを計算しましょう。

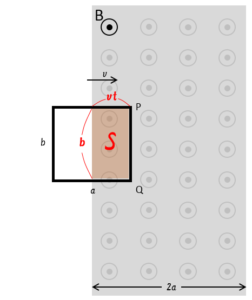
ここで、$\Phi=BS$、$t$ 秒間での図の面積 $S=(vt)\times b$ 、$v$、$b$ は一定として、
$\Delta \Phi=\Delta(BS)=B\Delta(vt\times b)=vBb\Delta t$

$(\:\:\Delta(a\cdot b)=\Delta a \cdot b +a \cdot \Delta b\:\:)$

したがって、ファラデー電磁誘導の法則から、

$V=\left| -\dfrac{\Delta \Phi}{\Delta t} \right|$

$~~~=\left| -\dfrac{vBb\Delta t}{\Delta t} \right|$

$~~~=vBb$

$I=\dfrac{V}{R}=\dfrac{vBb}{R}$

ここで、$P\: \rightarrow Q$ 方向を正としていることに注意してグラフを作成しましょう。

---

次図のような場合は、コイルを貫く上向き(画面から目の方向)の磁束が増加するので、コイルが下向き(目から画面方向)の磁束を作る方向へ電流が流れます。

このとき、電流の方向は、右手の規則で、$P \rightarrow Q$ の方向となります。

　　

---

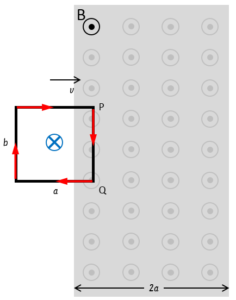
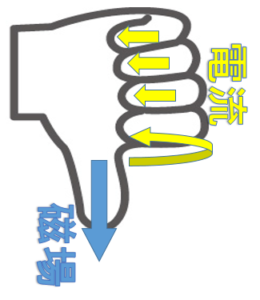
また、磁場からコイルが出ていくような場合はコイルを貫く上向きの磁束が減少するので、コイルが上向きの磁束を作る方向へ電流が流れます。

この場合、右手の法則を使って電流方向を求めると$Q \rightarrow P$ の方向となります。

 

---

時刻

• • $t=0$ とのき ・・・・・・コイルの右端は磁場に入ります。
  • $t=\dfrac{a}{v}$  ・・・ コイルは磁場の中に完全に隠れてしまいます。
  • $t=\dfrac{2a}{v}$・・・ コイルの右端は磁場の右端に達します。
  • $t=\dfrac{3a}{v}$ ・・・コイルは完全に磁場から脱します。

---

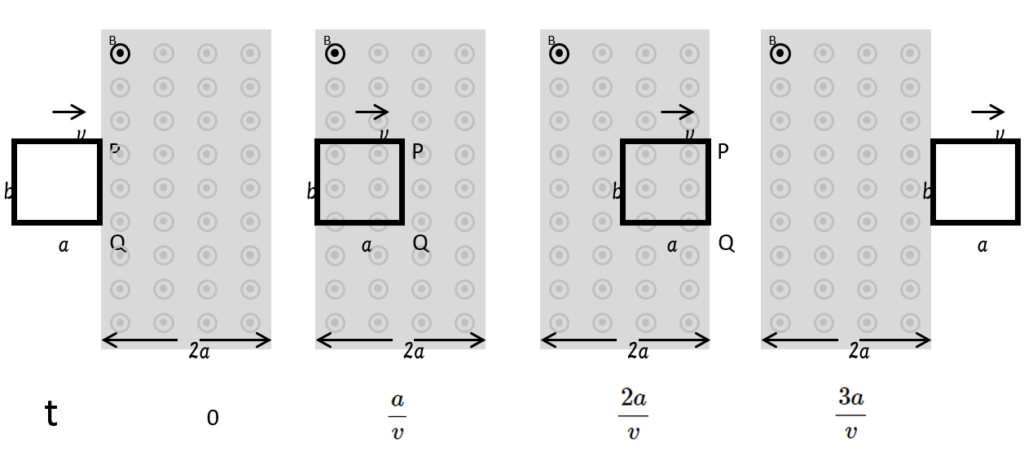
アニメーション

全体をアニメーションで示しました。

誘導電流のグラフ

以上より、電流－時間　のグラフは次のようになります。±に注意してください。

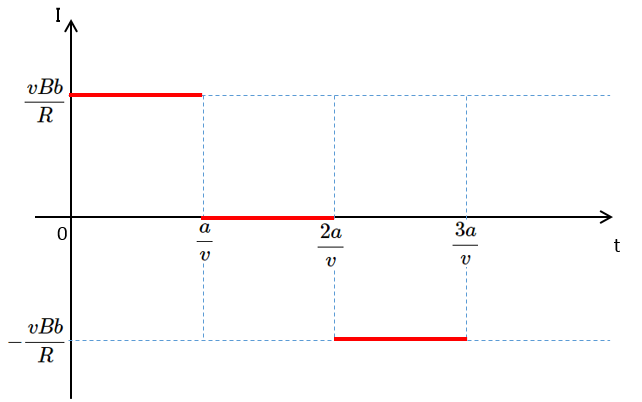
注意すべきなのは

• • コイルの誘導起電力は $V=vBb$ で、コイルが誘導起電力を発生している間は一定である。
  • したがって、誘導電流も、それが発生している間は一定の値を保つ。
  • よって、グラフは必ず $t$ 軸に平行になる。

外力

では、コイルを引くための外力の大きさと方向を考えます。
コイルが等速運動していることから、慣性の法則により、コイルにはたらく外力はつり合っているか、または、全くはたらいていないはずです。

コイルが磁場から受ける力の大きさは、$F$ とすると、$F=IBl$ と示せますから、$I=\dfrac{vBb}{R}$ の大きさの電流が流れているときは

$F=IBl=\left(\dfrac{vBb}{R}\right)\times B\times b$
$~~~=\dfrac{vB^2b^2}{R}$

となります。

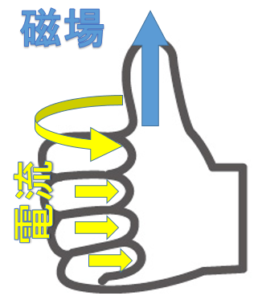
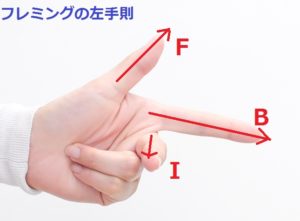
フレミングの左手則で考えると

コイルが磁場から受ける力の方向ですが、電流方向と磁場の方向からフレミング左手の法則で求められます。

エネルギーによる考えかた

しかし、次のように考えてもいいでしょう。
エネルギー保存則です。

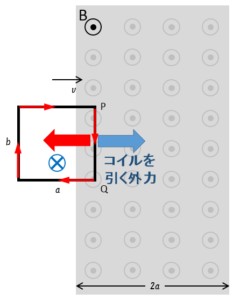
図でコイルを磁場に入れるときは、コイルに電気的なエネルギーを生じるのですから、どこかからエネルギーを調達せねばなりません。

そのエネルギーは、コイルを動かす手の仕事によるものです。
したがって、コイルが磁場から受ける力の方向は、図の左に向くはずです。
なぜなら、コイルを右向きに動かそうとする手が抵抗を感じて、それに逆らって仕事をする必要があるからです。

よって、コイルを引く外力は図の右向きにかける必要があります。

同様に、下図のコイルが磁場から出るときには、やはりコイルは磁場から下図の左向きに力を受けます。

ということは、コイルを引く外力は、やはり図の右向きにかける必要があります。

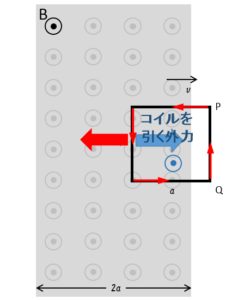
これらのとき、コイルにはたらく力の大きさ $F$ は、$I=\dfrac{vBb}{R}$ より、

$F=IBl=\left(\dfrac{vBb}{R}\right)\times B\times b$
$~~~=\dfrac{vB^2b^2}{R}$

となるのは同じです。

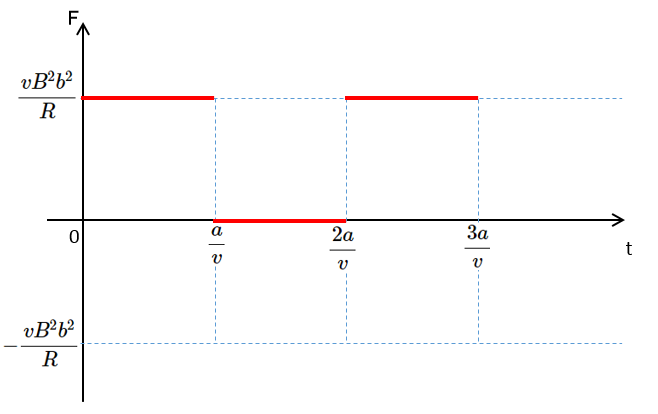
外力のグラフ

では以上を踏まえて、グラフを描いてみましょう。
必要な手が引く力は常に図の右向きです。（図の右向き正）

今回はこれでおしまいです。お疲れさまでした。

---

エッセンスの後は、良問、名問とすすむのがオススメです。

Amazon Amazon

Ｚ会Asteria　まずは無料でお試しください