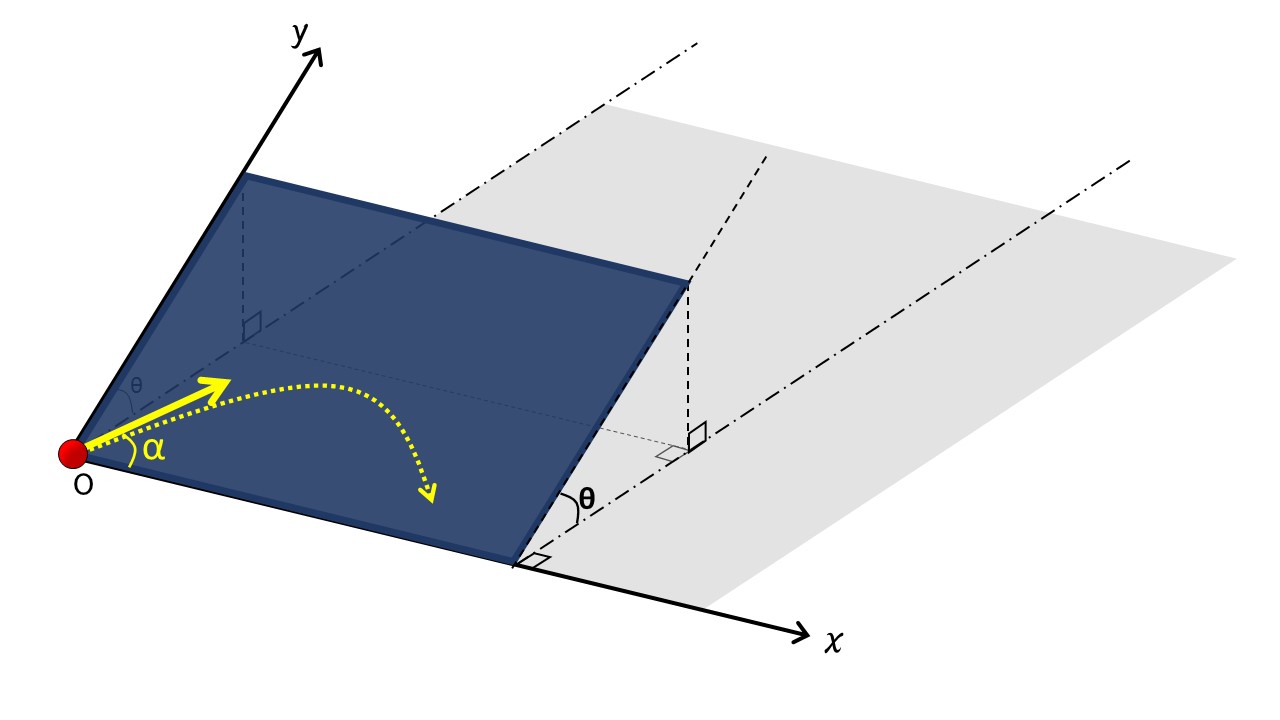
この問題の状況をイメージできるように、ちょっと頑張って図を描いてみました。
どうぞご参考にしてください。
物理のエッセンス解説 力学 9番 P13

物理のエッセンス 赤 力学・波動編 13ページ 9番
を参照してください。
問題 力学9番
図のように $x-y$ 座標を取り、その斜面上で $x$ 軸と角度 $\alpha$ になるようにボールを打ち出しました。
$y$ 軸のとり方に注意してください。
ボールは斜面上を運動し、飛び出したりしません。
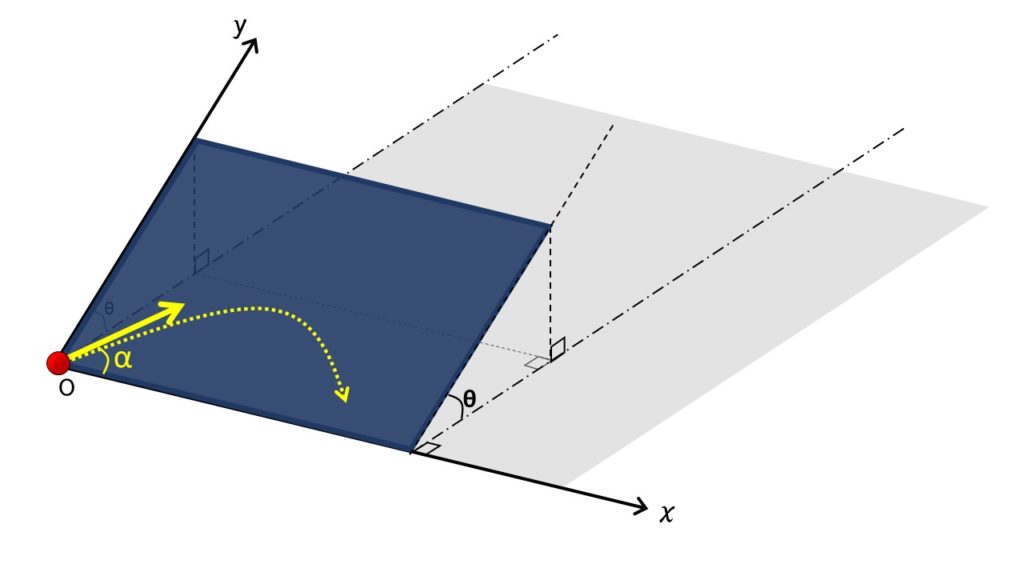
このとき、ボールが最高点に達するまでの時間 $t$ を求めよ。
というのが問題になります。
要は、図のように青い板を水平面から角度 $\theta$ だけ傾けた斜面上で、ボールを打ち出したというだけのことです。
解説
問題の意図する状況が理解できてイメージできさえすれば、それほど難しい問題ではありません。
では、解説に入りましょう。
ボールは斜面上を「放物運動」します。
まず、斜面上での初速度 $v_0$ を $x$ 軸と $y$ 軸方向に分解します。
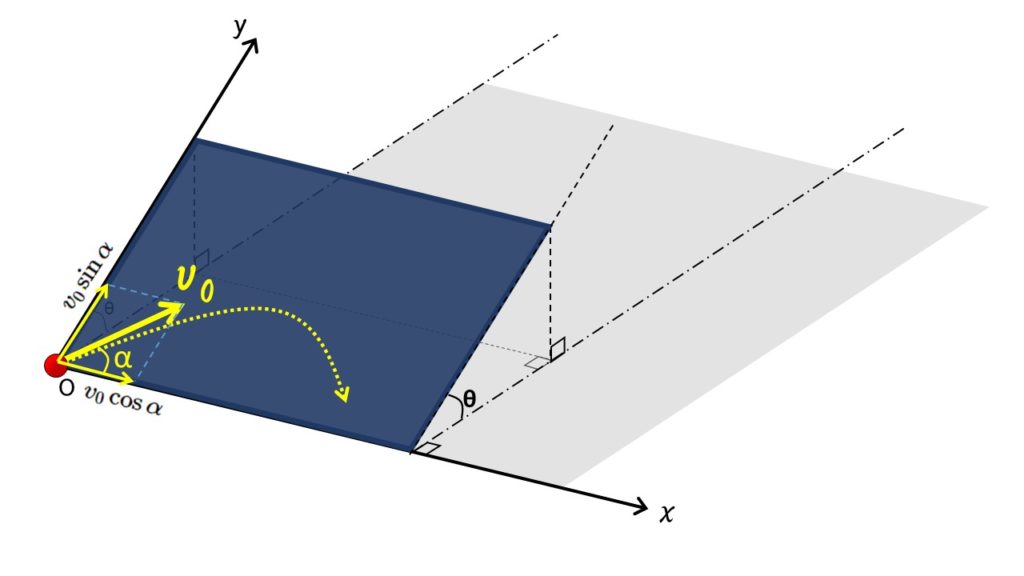
さて、ここからどうするか・・・ですが、ちょっと視点を変えて $x$ 軸の方向から眺めてみましょう。
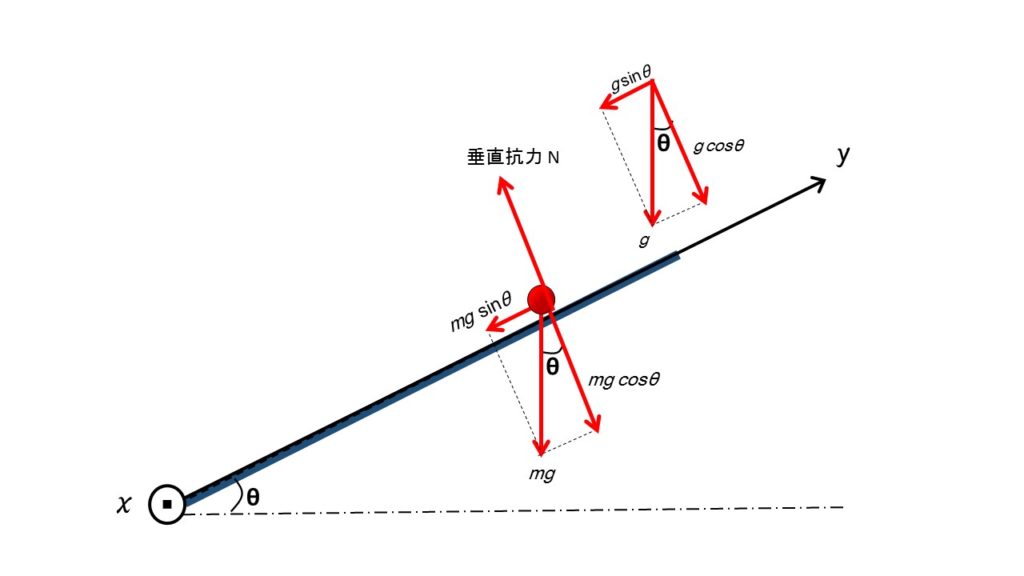
そこで、斜面上を運動している物体にはたらく重力を $y$ 軸方向と斜面に垂直な方向に分解します。
図で明らかなように、重力の斜面に垂直な方向の力 $mg \cos \theta$ と垂直抗力 $N$ は打ち消し合います。
このとき、斜面上の世界を考えてみます。
この世界では、重力加速度は斜面方向だけを考えればよく、その大きさは重力加速度 $g$ の $y$ 方向を考えて、$g\sin\theta$ となります。
では次の図を見てください。
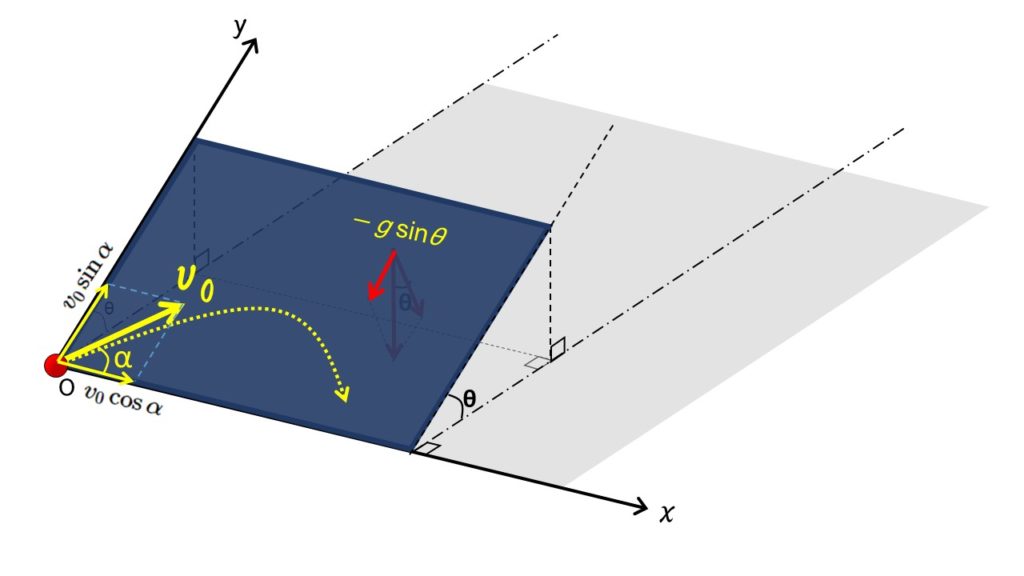
そうすると、正負も考えて、この世界での重力加速度は $-g\sin\theta$ で、$y$ 軸方向の初速度を $v_0\sin\alpha$ と考えれば良いことになります。
解き方は普通の斜方投射と同じです。ただ、重力加速度を $-g\sin\theta$ とするだけです。
最高点では $y$ 軸方向の速度が $0$ となることから、最高点に達するまでの時間を $t$ とすると、$v=v_0+at$ より、
$0=(v_0\sin\alpha)+(-g\sin\theta)\times t$
$t=\dfrac{v_0\sin\alpha}{g\sin\theta}$
となります。
もしも、最高到達点の高さを聞かれた場合は、
斜面上での最高到達点の高さ( $y$ の値)を求めて、それを $\sin\theta$ 倍すればよいでしょう。

その他、応用的な問題がでても、
理解できていれば対応可能なはずです。
頑張りましょう!

エッセンスを終えたら、
良問・名問 がオススメ

YouTubeでも解説等の動画をアップしています
よろしければ、チャンネル登録お願いします!





































コメント
独学で物理を勉強しているものです。
問題の図が平面なのでイメージすることができず、「物理のエッセンス9」と検索したところこのページに辿りつきました。
動画を見て明確にイメージすることができ、助かりました。
ここで、質問なのですが
動画で使用しているツールとまた図形を作成している際のツールについて教えていただけますでしょうか?
私もsketchというツールを利用して、自身の学習のために数学の定理の証明を自身のサイトにアップしているのですが、
図形を作る際にもっといいツールがないかなぁーと思っています。
以上、よろしくお願いします。
コメントありがとうございます。
動画作成のツールですが、BBFlash Back PRO です。
図形作成は、パワーポイントです。特別なものを使っていません。
パワポは目的が違いますから、図形作成に関しては扱いやすいとはいえないかもしれません。
返信ありがとうございます。
>図形作成は、パワーポイントです。特別なものを使っていません。
パワーポイントで作っているんですね、そういう使い方もあるんですね。
>動画作成のツールですが、BBFlash Back PRO です。
やはり、有償になってしまうんですね。
自分もここで数学定理をメモしているんですが、図形を書くのになかなか時間がかかってしまいます。
早く作る方法がないかなと思っているんですが…
https://www.gamecorder.net/math/index.php
物理のエッセンスに詰まった際などまた参考にさせていただきます。
ありがとうございました。
ところで、
質問の内容からして、問合せの項目から送った方がよかったと思うし、
urlも載せたので、コメントは削除してしまって大丈夫です。
あと、ページの一番下のcopy rightのところなんですが、「高校物理.」
となっているようです。
以上、おせっかいだったらすいません、応援してます。
ご連絡ありがとうございます。
図形作成に関しては私ももっといいものがほしいです。
なにかあれば教えていただけるとありがたいです。
また、「高校物理.」の件ありがとうございました。
気がつきませんでした。
今後ともよろしくお願いいたします。