これも $v-t$ グラフを描いて考えてみましょう。
物理のエッセンス力学編11番
問題概要
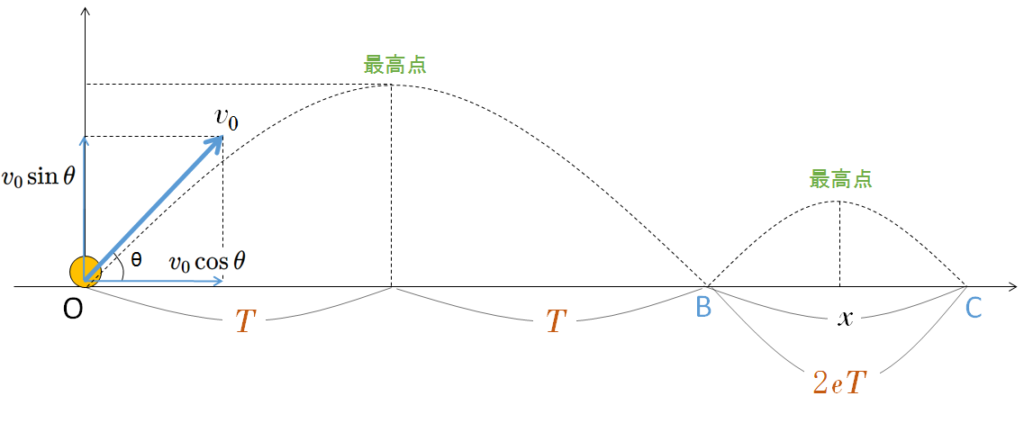
水平な床から角 $\theta$ の方向に物体を初速 $v_0$ で投げだす。
床との最初の衝突点を B 、2度目の衝突点を C としたとき、BC間の距離を求める。
物体と床との反発係数を $e$ 、重力加速度の大きさを $g$ とする。
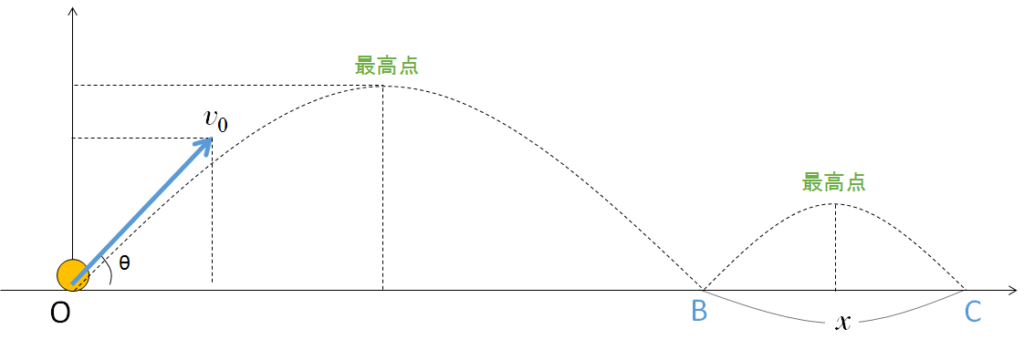
解説
式を使った計算は本の解答解説にまかせて、ここではこれまでやってきたように $v-t$ グラフを描くことで考えて見ます。
水平な床から斜めに角 $\theta$ で物体を投げるのですが、鉛直方向と水平方向に分けて考えます。
そうすると、次の図から、
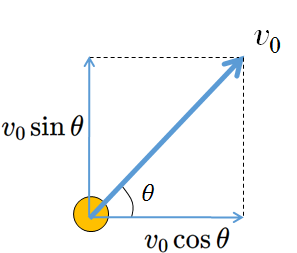
鉛直方向の初速度 $v_0\sin\theta$
水平方向の初速度 $v_0\cos\theta$
となることがわかります。
鉛直方向
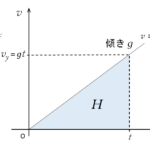
鉛直方向では鉛直上方に初速度 $v_0\sin\theta$ 、加速度 $g$ (鉛直下方)であることから、$v-t$ グラフは次のようになります。
このグラフの傾きは全て $-g$ (大きさ $g$ )です。
そして、物体が床と衝突したあとの物体の速さは $e$ 倍、すなわち $ev_0\sin\theta$ となります。
つまり、床と衝突するごとに $e$ 倍されていくと考えられます。
$v_0\sin\theta \: \rightarrow \: ev_0\sin\theta\:\rightarrow \:e^2v_0\sin\theta\:\rightarrow\:\cdots\cdots $

反発係数 $e$
$e=-\dfrac{v’}{v}$
$v’=-ev$
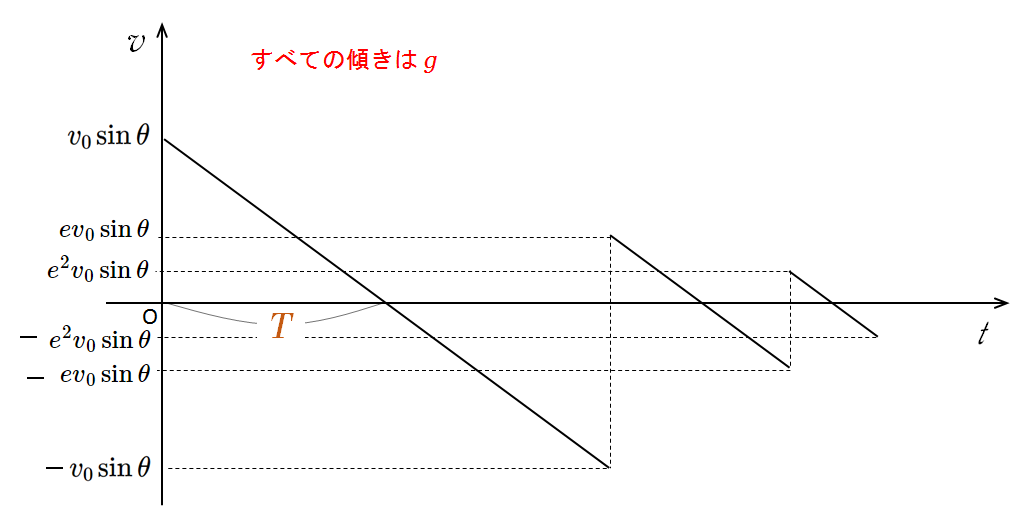
物体を打ち出してから最高点に到達する時間を $T$ とすると、グラフから
$\mathrm{グラフの傾きの大きさ}=g=\dfrac{v_0\sin\theta}{T}$
よって、 $T=\dfrac{v_0\sin\theta}{g}$ となります。
そして、傾きが同じなため、このグラフにおいて、$t$ 軸とグラフの作る三角形はすべて相似です。
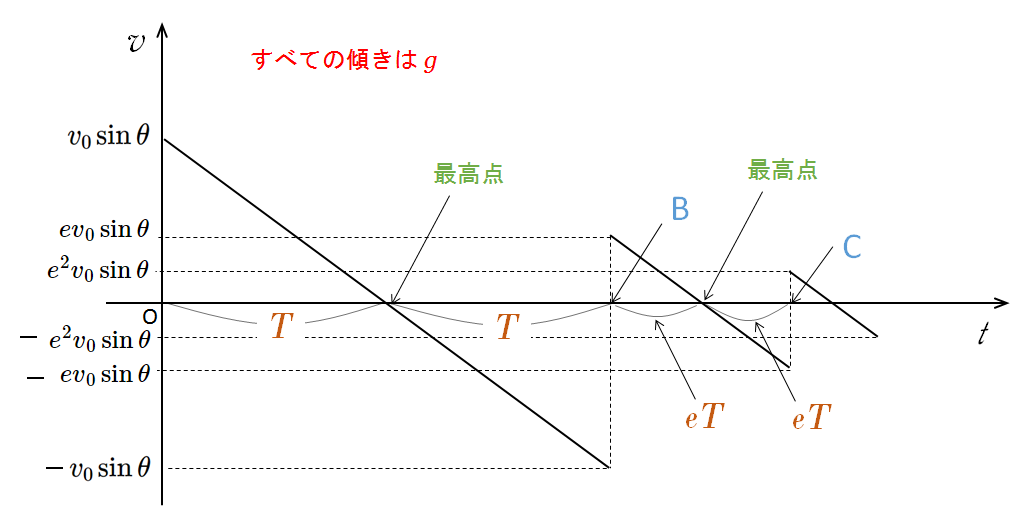
先述べたように三角形はすべて相似のため、最初に床と衝突した物体が鉛直方向に最高点に到達する時間は、$T$ の $e$ 倍、
すなわち
$eT=e\dfrac{v_0\sin\theta}{g}$
です。
なので、BC間を運動するのに必要な時間 $T_{BC}$ は $T_{BC}=2\times eT$ となります。
$T_{ BC}=2\times eT=2 e\dfrac{v_0\sin\theta}{g}$
水平方向
床と物体の間に摩擦が無いため、物体は水平方向には速さ $v_0\cos\theta$ で等速運動します。
したがってその距離は $x=vt$ で示されます。
鉛直方向の考察により、BC間を運動するのに必要な時間は $T_{BC}$ であるので、
$x=v_0\cos\theta \times T_{BC}$
より、

$T_{ BC}=2\times eT=2 e\dfrac{v_0\sin\theta}{g}$
$x= v_0\cos\theta \times \left (2e\dfrac{v_0\sin\theta}{g} \right )$
$~~~= 2 e\dfrac{v^2_0}{g}\sin\theta\cos\theta$
$~~~=\dfrac{ev^2_0}{g}\sin 2\theta$

$2\sin\theta\cos\theta = \sin 2\theta$ を使いました。

ちなみに、$\sin2\theta = 1$ のとき $x$ は最大になります。
つまり、$\theta =45^{\circ}$ のときです。





































コメント