必殺技による 動画解説エッセンス　コンデンサー30* P59

物理のエッセンス 電磁気編 コンデンサー 問題30*　について解説

この解説ではエッセンスで推奨されている「必殺技」を用いています。
これは非常に有用な方法といえるでしょう

kareni / Pixabay

また、簡単にその「必殺技」についても説明していますのでご参考に！

この必殺技を使うと、たちどころに問題を解くことができてしまうことが多いのですが、一般的な方法についてしっかりと理解をしておくことが必要です。

最後にものを言うのはテクニックより基本理解ですから。

エッセンスの次は良問、そして名問がおすすめです。
Amazon Amazon

動画解説

コンデンサーの極板上の電気量計算（必殺技基本）

コンデンサーの片方の極板における電気量を計算するには次のように行います。

$Q=CV$

より考えます。

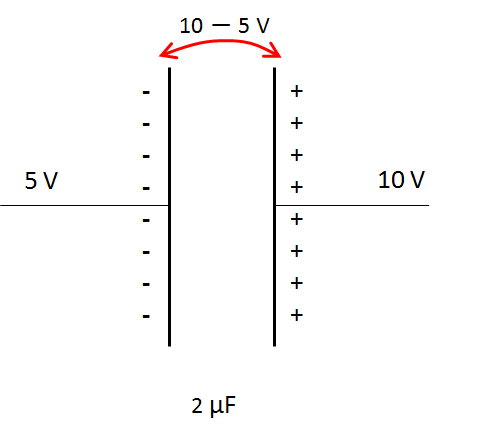
この 右側の極板に貯まる電気量は 

\begin{eqnarray}
Q&=&CV\\
&=&2\times(10-5)\\
&=&+10\mu C\\
\end{eqnarray}

となり、$+$ の値を持ちます。

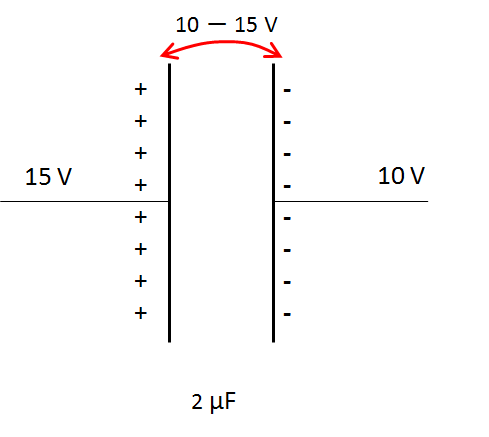
同様に 右側の極板に貯まる電気量は 

\begin{eqnarray}
Q&=&CV\\
&=&2\times(10-15)\\
&=&-10\mu C\\
\end{eqnarray}

となり、$-$ の値を持ちます。

つまり

$$Q=C(V_{自分}-V_{相手})$$

とすることで極板に貯まる電気量を正負まで含めて計算できるのです。

必殺技による問題解説

この問題の場合、図の $3\mu F$ のコンデンサーに貯まる電気量を計算します。

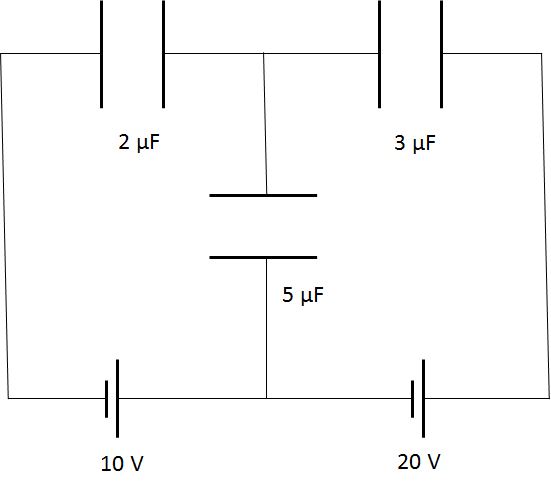
このような場合、いくつかのやり方はありますが、まずは下の図のように赤い部分に着目します。この赤く囲った部分の総電気量は電池をつないでも変化しません。
（各コンデンサーの電気量はもちろん変化します）

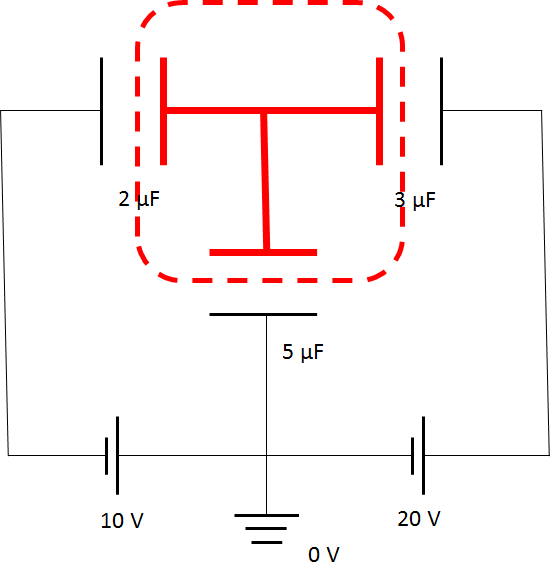
したがってこのことを利用するのですが、このとき上の図にあるように $0 V$ を適当に想定します（アースを設置します）。

アースを設置する位置はどこでもいいのです。なぜかと言うと必要なのはコンデンサーの極板間にかかる電圧です。
つまり、極板間の電位の差さえわかればよいのです。

その上で次の図のように3つのコンデンサーの電位を $x$ と仮定します。
その上で各コンデンサーの赤色側の極板の電気量をそれぞれ、$Q_1\:\:Q_2\:\:Q_3$ としてやります。

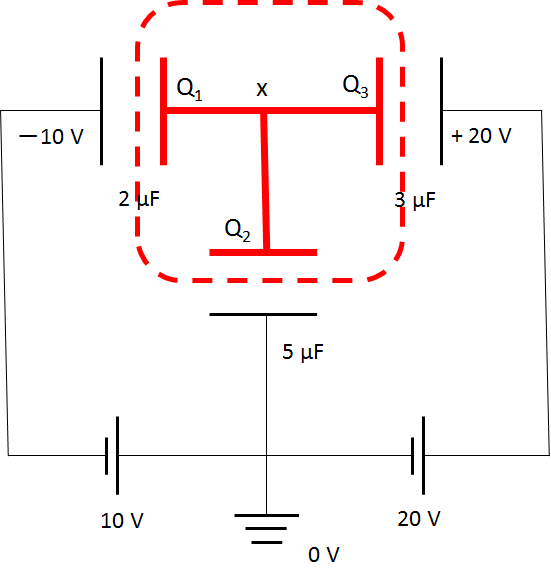
赤色の中の電気量の総和は $0$ ですから、

$Q_1+Q_2+Q_3=0$

です。したがって、$Q=C(V_{自分}-V_{相手})$ より

\begin{eqnarray}
Q_1+Q_2+Q_3&=&0\\
&=&2\times\{x-(-10)\} + 5\times(x-0)+3\times(x-20)\\
&=&0
\end{eqnarray}

より、$x=4$ を得ます。
したがって、$3\mu F$ のコンデンサーに貯まる電気量は、

$Q=3\times |4-20|=48 \mu C$

となります。

この方法は時間を非常に短縮することが可能です。
コンデンサーの解法として身につけておいて損はありません。

言うまでもありませんが、コンデンサーの基本基礎をしっかりと理解した上で用いてくださいね。

エッセンスの次は良問、そして名問がおすすめです。
Amazon Amazon