物理のエッセンス 力学46番
「物体を引くロープの質量が無視できる」というのが多くの問題のお約束ですが、この問題では、ロープの質量を $m$ ,長さを $l$ としています。
その場合の、物体とロープの接合点から $x$ だけ離れた位置でのロープの張力を求めます。
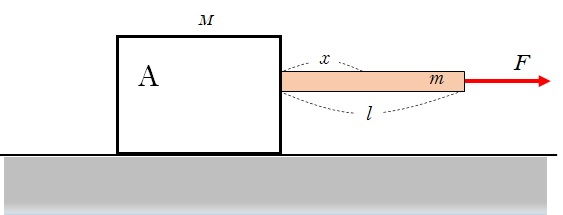
ロープの張力はどこでも同じ・・・として問題を解くことがほとんどです。
でも、なぜロープ張力はどこでも同じなんでしょうか?
それはロープの質量が
物理のエッセンス 力学46番
「物体を引くロープの質量が無視できる」というのが多くの問題のお約束ですが、この問題では、ロープの質量を $m$ ,長さを $l$ としています。
その場合の、物体とロープの接合点から $x$ だけ離れた位置でのロープの張力を求めます。

ロープの張力はどこでも同じ・・・として問題を解くことがほとんどです。
でも、なぜロープ張力はどこでも同じなんでしょうか?
それはロープの質量が $0$ とみなせる、としているからなのですが、・・・・
こちらの記事も参考にしてください。いまさら聞けない!なぜ張力は同じなのか?
解説
$ とみなせる、としているからなのですが、・・・・
こちらの記事も参考にしてください。いまさら聞けない!なぜ張力は同じなのか?
解説
力の描き入れ

ロープの張力はどこでも同じ・・・として問題を解くことがほとんどです。
でも、なぜロープ張力はどこでも同じなんでしょうか?
それはロープの質量が
物理のエッセンス 力学46番
「物体を引くロープの質量が無視できる」というのが多くの問題のお約束ですが、この問題では、ロープの質量を $m$ ,長さを $l$ としています。
その場合の、物体とロープの接合点から $x$ だけ離れた位置でのロープの張力を求めます。

ロープの張力はどこでも同じ・・・として問題を解くことがほとんどです。
でも、なぜロープ張力はどこでも同じなんでしょうか?
それはロープの質量が $0$ とみなせる、としているからなのですが、・・・・
こちらの記事も参考にしてください。いまさら聞けない!なぜ張力は同じなのか?
解説
$ とみなせる、としているからなのですが、・・・・こちらの記事も参考にしてください。いまさら聞けない!なぜ張力は同じなのか?
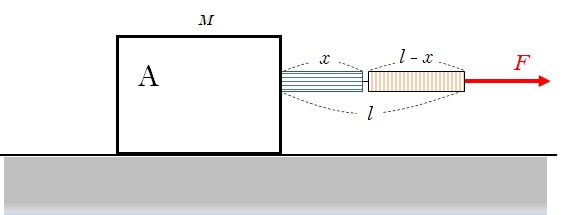
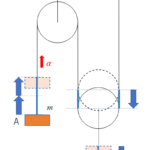
ロープにも無視できない質量 $m$ があることから、図のようにロープを青とオレンジの2つの部分に分けます。
そして、青い部分とオレンジ部分を質量を無視できる糸で連結します。
ただし、ロープは水平を保つとします。
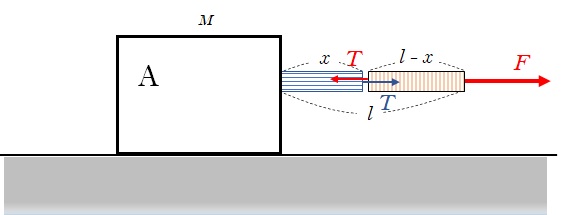
その糸の張力を $T$ として、ロープの青とオレンジにはたらく張力を図に描き入れます。
この場合の糸の張力 $T$ はどこでも同じです。
ここで、
質量 $m$ のロープを $x$ と $l-x$ の部分に分けていることから、
・青の部分の質量 $:$ オレンジの部分の質量 $=x:(l-x)$
・青の部分の質量 $+$ オレンジの部分の質量 $=m$
です。
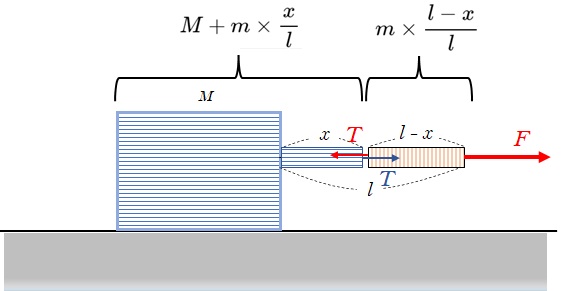
さて、ここで青の部分を拡大して、質量 $M$ の部分も含めてしまいましょう。
そうすると、図の青の部分の質量は $M + m\times \dfrac{x}{l}$ ,
ロープのオレンジ部分は $m\times \dfrac{l-x}{l}$ です。
運動方程式
青とオレンジの部分について、加速度を $a$ として運動方程式をたてます。
ちなみに、この場合、青とオレンジ部分の加速度は同じです。
$ma=F$ より、
オレンジ:$\left(m \dfrac{l-x}{l} \right )a=F-T \:\:\:\dots\:(1)$
青 :$\left ( M+m\dfrac{x}{l}\right)a=T \:\:\:\dots\:(2)$
これらを解いて $T$ を得ます。
ここでは、(1)÷(2) としてみます。
$\dfrac{(1)}{(2)}=\dfrac{\left(m \dfrac{l-x}{l} \right )a}{\left ( M+m\dfrac{x}{l}\right)a}=\dfrac{F-T}{T}$
より、
$\dfrac{m(l-x)}{Ml+mx}=\dfrac{F}{T}-1$
よって、
$\dfrac{F}{T}=\dfrac{m(l-x)}{Ml+mx}+1$
$\:\:\:\:\:\:\,=\dfrac{ml-mx+Ml+mx}{Ml+mx}$
$\:\:\:\:\:\:\,=\dfrac{(M+m)l}{Ml+mx}$
よって、
$T=\dfrac{Ml+mx}{(M+m)l}F$





































コメント
今回の問題には直接関係無いかもしれまんが、質量のあるロープの場合、物体Mとロープの左端には垂直抗力が働いていますか?
気が付きませんでした。おそくなりすみません。
質問の意味がよくわかりませんが,ロープが物体を引く力と物体Mがロープを引く力があります。