あの天才ノイマンも同じような問題を出題され、そして即座に正答したという逸話が残っています。
ここでは、一瞬で解く方法と、真面目に計算する方法の二通りで答えを出してみたいと思います。
ノイマンはどのように考えたのでしょうか?
ノイマンも考えた問題
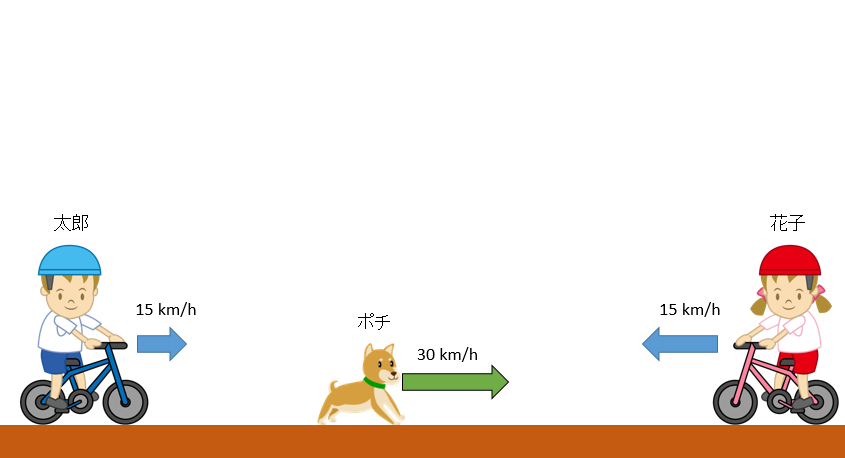
太郎と花子は友達です。
ある日、太郎が真っ直ぐな道路上で自転車を漕いでいると、ちょうど $3\: \mathrm{km}$ 向こうから花子が同じく自転車に乗ってやってくるのが見えました。
自転車を漕ぐ速さは太郎が $15\:\mathrm{km/h}$、花子も $15\:\mathrm{km/h}$ です。
ふたりとも出合うまでずっと等速で進みます。
さて、太郎はそのとき犬のポチを連れていましたが、ポチは花子が大好きです。
太郎が花子を見つけた瞬間、ポチは太郎のもとから花子のもとへ速さ $30\:\mathrm{km/h}$ でダッシュして走っていきます。
ポチは花子のもとへ着くと瞬間的に反転して太郎のもとへ向かいます。
ポチは運動能力が高く、一瞬でその速度を変えられるのですね。
太郎のもとへ帰ったポチはまた瞬間的に反転して花子のもとへ向かいます。
こうして、ポチは二人が出合うまで二人の間を行ったり来たりを続けます。
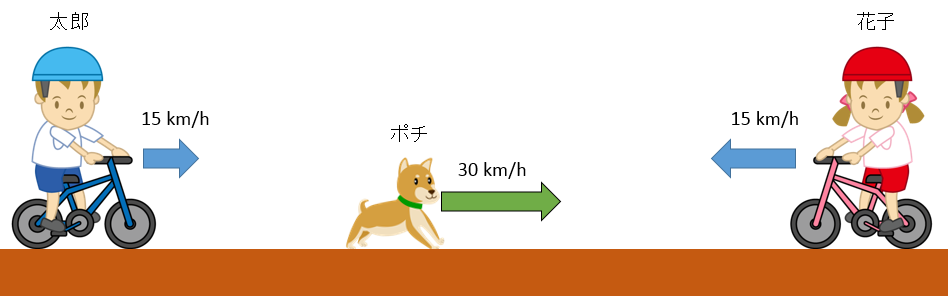
さて、問題です「二人が出合うまでのポチはどれだけの距離を走ったでしょうか?」
答えを見る前にぜひ少し考えてみて下さい。

答え
答えは $3\:\mathrm{km}$ です。ちなみに一瞬で答えが出ます。
相対速度で考えると、太郎は $15+15=30\:\:[\mathrm{km/h}]$ で進み、花子は静止していると考えて差し支えありません。
つまり、二人が出合うまでの時間は、 $3\:[\mathrm{km}]\div (15+15)\:[\mathrm{km/h}]=\dfrac{3}{30}=\dfrac{1}{10}\:\:[\mathrm{h}]$ ですね。
その間、ポチは $30\: \mathrm{km/h}$ の同じ速さで走り続けているわけですから、ポチの走る距離は単純に、 速さ×時間 より、
$ポチの走る距離=\dfrac{1}{10}\:[\mathrm{h}]\times 30\:[\mathrm{km/h}]=3\:\:[\mathrm{km}]$
となり、答えは $3\:\mathrm{km}$ です。
まじめに計算してみよう
この問題は上に述べたように「答え」の方法で行うと一瞬で計算することが可能です。
しかし、ここでは無限級数を考えて「真面目に」解いてみましょう。
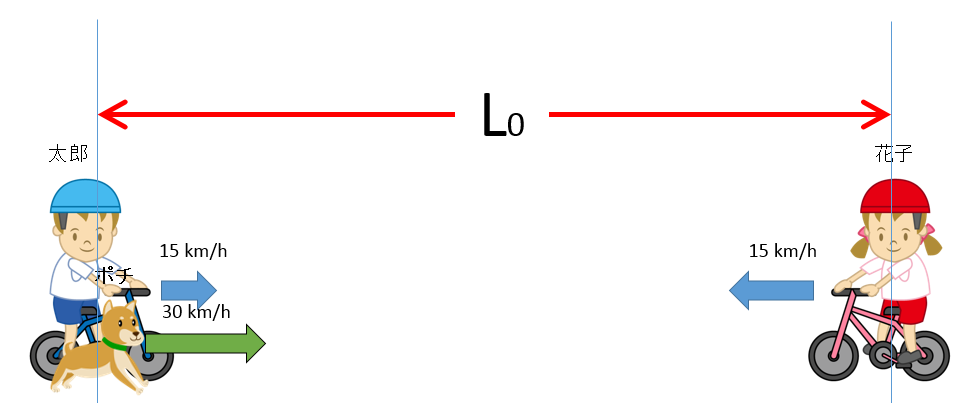
太郎と花子が距離、$L_0$ 離れているとします。
ポチが太郎から花子に向かうとき、花子に対するポチの相対速度の大きさは、 $30+15\:\:[\mathrm{km/h}]$ です。
したがって、ポチは $t=\dfrac{L_0}{(30+15)}=\dfrac{L_0}{45}\:\:[\mathrm{h}]$ の時間だけ走ります。
よって太郎から花子までポチの走る距離 $x_0$ とすると、 $x_0=L_0-15t=L_0-15\times \dfrac{L_0}{45}=\dfrac{2}{3}L_0\:\:[\mathrm{km}]$ です。
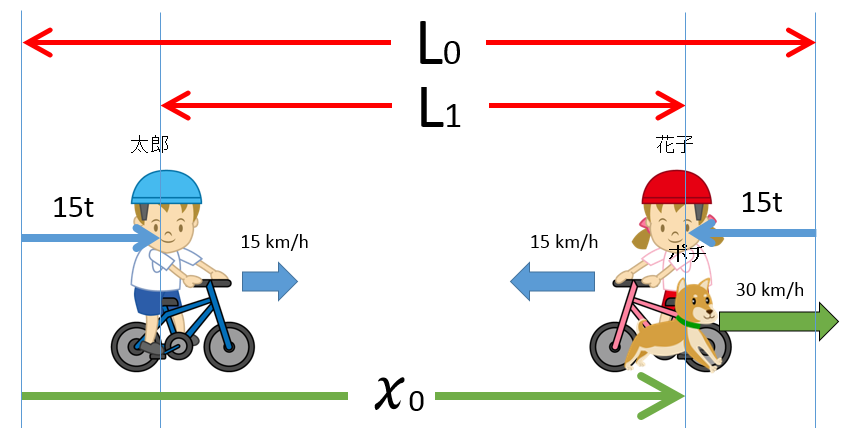
そして、ポチが走っている間に二人はさらに、 $t\times 15+t\times 15=30t \:\:[\mathrm{km}]$ だけ近づきますから、ポチが花子のもとについた瞬間には二人の距離 $L_1$ は、
$L_1= L_0-30t=L_0- 30\times \dfrac{L_0}{45}=L_0-L_0\times \dfrac{2}{3}=\dfrac{1}{3}L_0 \:\:[\mathrm{km}]$ になっているはずですね。
次にポチが花子から太郎に向かう場合を考えます。
この問題の場合、太郎と花子の速さは同じですから、答えは上と同じ形になるはずですが一応やってみましょう。
太郎に対するポチの相対速度の大きさは、 $30+15\:\:[\mathrm{km/h}]$ です。
今二人の距離は $L_1$ だけ離れていますから、ポチは今度は $t’=\dfrac{L_1}{(30+15)}=\dfrac{L_1}{45}\:\:[\mathrm{km}]$ の時間だけ走ります。
よってこのとき、太郎までのポチの走る距離 $x_1$ は、 $x_1=L_1-15 \times t’=L_1-15\times \dfrac{L_1}{45}=\dfrac{2}{3}L_1\:\:[\mathrm{km}]$
そしてその時の二人の距離 $L_2$ は、 $t’\times 15+t’\times 15=30t’ \:\:[\mathrm{km}]$ だけ近づきますから、
$L_2=L_1-30t’=L_1-30\times \dfrac{L_1}{45}=\dfrac{1}{3}L_1\:\:[\mathrm{km}]$
です。
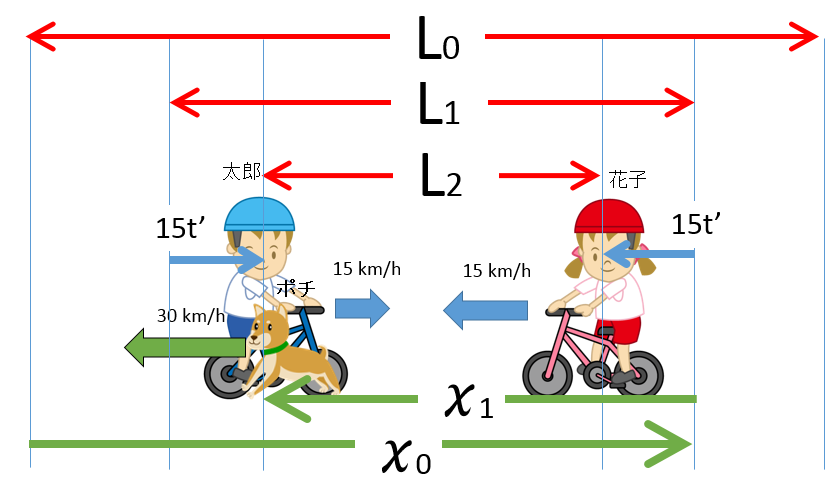
以上から、ポチは二人の距離が $L_n$ のとき、 $\dfrac{2}{3}L_n$ だけ走ります。($n=0,1,2,3,4,\cdots$)
そして、 $L_{n+1}=\dfrac{1}{3}L_{n}$ です。
したがって、ポチの走る距離 $x_p$ は、
\begin{eqnarray}
x_p&=&x_0+x_1+x_2+\cdots \cdots \\\\
&=&\dfrac{2}{3}L_0+\dfrac{2}{3}L_1+\dfrac{2}{3}L_2+ \cdots \cdots \\\\
&=&\dfrac{2}{3}\left(L_0+L_1+L_2+\cdots \cdots \right)\\\\
&=&\dfrac{2}{3}\left(L_0+\dfrac{1}{3}L_0+\dfrac{1}{9}L_0+\dfrac{1}{27}L_0+\cdots \cdots \right)\\\\
&=&\dfrac{2}{3}L_0\left(1+\dfrac{1}{3}+\dfrac{1}{9}+\dfrac{1}{27}+\cdots \cdots \right)\\\\
&=&\dfrac{2}{3}L_0\dfrac{1}{1-\dfrac{1}{3}}\\\\
&=&L_0\:\:[\mathrm{km}]
\end{eqnarray}
よって、$x_p=L_0$ 、ここで $L_0=3\:\:[\mathrm{km}]$ なので、 $x_p=3\:\:[\mathrm{km}]$ です。
ノイマンの逸話
伝説の天才、ジョン・フォン・ノイマンは逸話に事欠きません。
- 子供のときに電話帳を眺め、ページ全てを暗算で足して遊んでいた。
- コンピュータを開発し、その自らが生み出したコンピュータと暗算で勝負して勝った。
- ある数学者が苦心惨憺何ヶ月も考え抜いた問題が解け、嬉しさのあまりノイマンに説明していると、それまで何も知らなかったノイマンが説明をさえぎって答えを出した。この数学者の落ち込み具合はハンパじゃなかったとか・・・。
など、人類であることが疑わしいとまで言われた人物です。
そのノイマンが、この記事のような問題を出され即座に答えたそうですが、その時の受け答えが・・・・
同僚のウラムがこの問題をノイマンに出す。
ノイマンが即座に答える。
ウラム「そうか。君もやっぱり知ってたんだな!」
ノイマン「知ってるって、何を?」
ノイマン「ただ、数列の和を出すだけじゃないのか?」
ウラム「・・・・・!」
以下はオススメの問題集・参考書などです。
また、映像授業についてもご紹介しています。


















コメント