直感は正しいか? 斜面を滑る物体
次の問題を考えてみましょう。
状態 1), 2) において、板が床面から受ける垂直抗力の大きさは同じでしょうか?
それとも違うのでしょうか? ただし、小物体が運動中に板は静止していたとします。
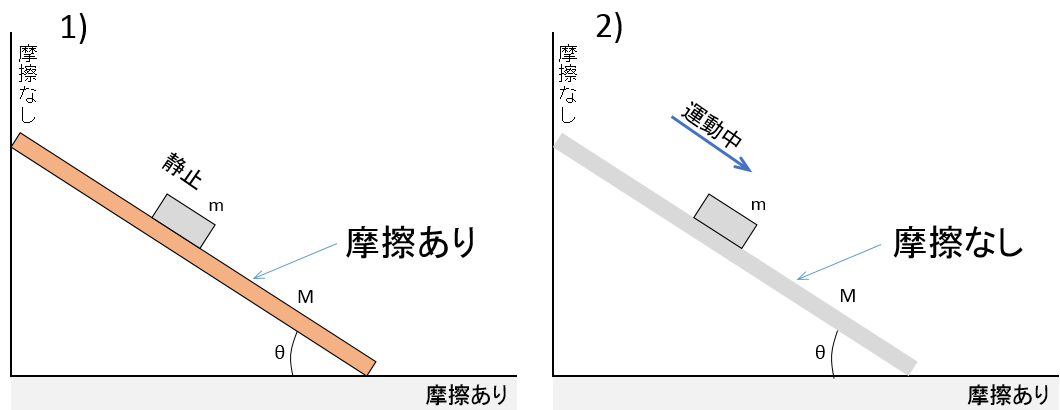
床と板の間には摩擦があります。
板と壁には摩擦がありません。
また、板の上には質量 $m$ の小物体が乗っており、1) ではそれらの間には摩擦がありますが、2) ではありません。
1). 質量 $M$ の摩擦のある剛体の板の上に質量 $m$ の小物体が静止している。
2). 質量 $M$ の摩擦のない剛体の板の上で質量 $m$ の小物体が板にそって滑っている。
選択肢
- 同じ
- 1)のほうが大きい
- 2)のほうが大きい
- 小物体の位置による
理由を考えましょう。

答え
それとも違うのでしょうか? ただし、小物体が運動中に板は静止していたとします。

板と壁には摩擦がありません。
また、板の上には質量 $m$ の小物体が乗っており、1) ではそれらの間には摩擦がありますが、2) ではありません。
2). 質量 $M$ の摩擦のない剛体の板の上で質量 $m$ の小物体が板にそって滑っている。

答えは、
板の受ける垂直抗力は 1) のほうが大きいです。
一見同じだと考えてしまう人が多いようです。
なぜ勘違いをしてしまうのかと言うと、教科書や問題集でよく見る問題は、そのほとんどで小物体が静止しています。なので、一般には板と小物体を一体化して考えることが通例です。
ここが盲点になりがちなところです。
物体が静止しているなら一体化しても問題はありません。
ここでは、小物体と板を一体化せず、分離して考えてみましょう。
1) について
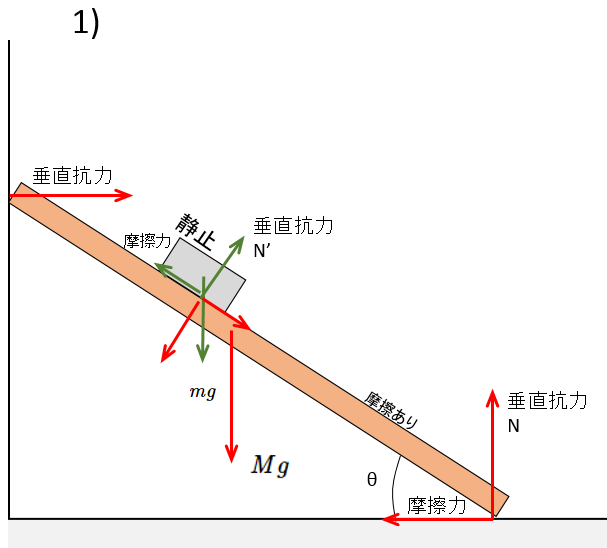
小物体にはたらく力は図の緑色の矢印で示されています。
このとき、小物体には摩擦力が働いているため静止しています。
板が受ける力のみを描いてみると次の図になります。
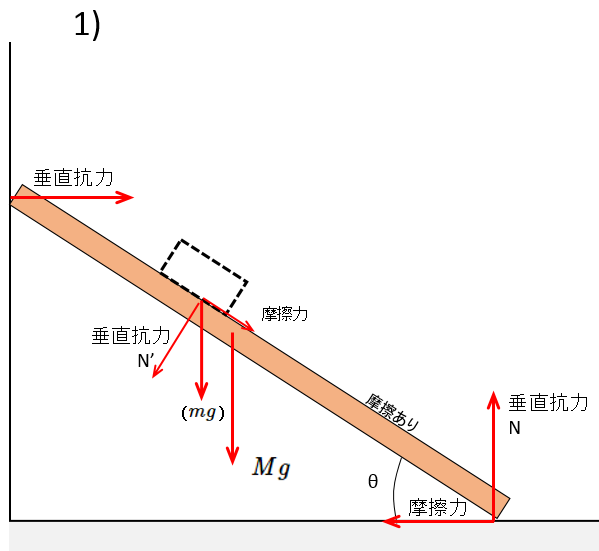
板が小物体から受ける力は垂直抗力 $N’$ と摩擦力ですから、その大きさは合成すると結局小物体の重さ $mg$ に等しくなります。( $N’$ も摩擦力も、ともに小物体が受ける力の反作用です)
したがって、板と小物体を合体させて考えても OK というわけです。
板が床から受ける垂直抗力 $N$ は、鉛直方向のつり合いから、
$N=Mg+mg$
となります。
2) について
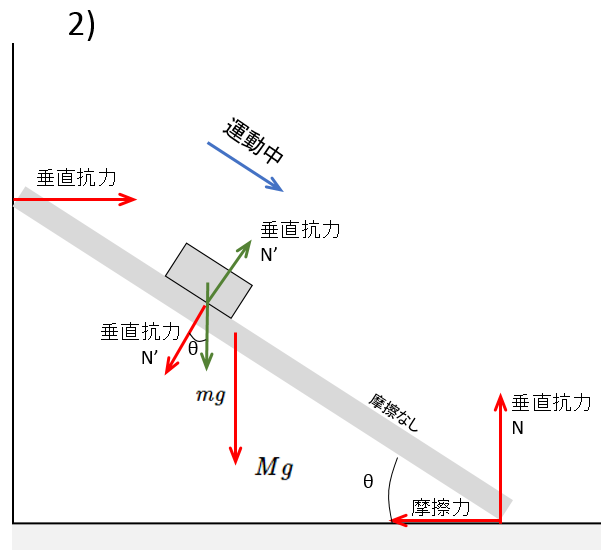
板と小物体には摩擦がありません。したがって小物体が受ける力は重力 $mg$ と垂直抗力 $N’$ のみです。
このとき、次の図に示すように板が受ける力だけを描いてみます。
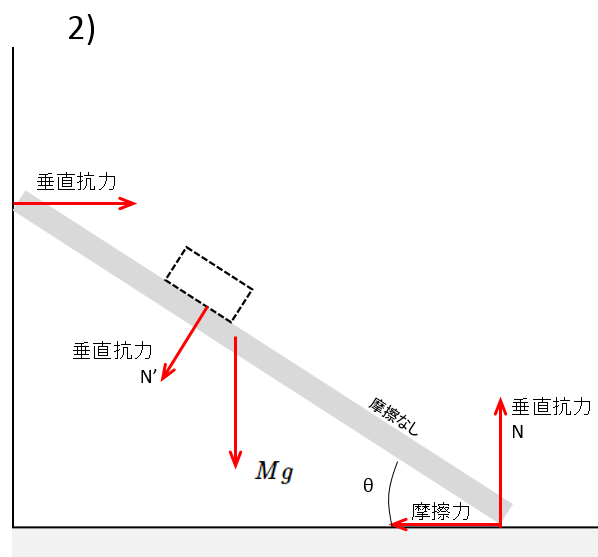
そうすると、板が小物体から受ける力は小物体が受ける垂直抗力 $N’$ の反作用だけです。
この力を鉛直方向と水平方向に分解してみます。
垂直抗力 $N’$ の大きさは小物体に関するつり合いから $N’=mg\cos\theta$ です。
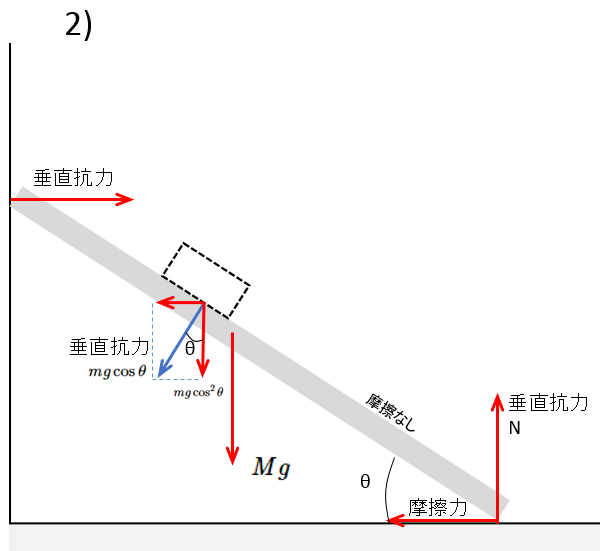
そうすると鉛直方向へは $N’=mg\cos\theta$ の $\cos$ 成分、すなわち $mg\cos^2\theta$ となります。
板が受ける力の鉛直方向へのつり合い式を立ててみると、
$N=Mg+mg\cos^2\theta$
なので、物体が静止している 1) の場合の垂直抗力の値 $Mg+mg$ と比較すると、2) の場合の垂直抗力 N のほうが小さくなりますね。





































コメント