ここでは、波長を基準としたドップラー効果の式について解説します。
こういう視点もあるということをぜひ知っていただきたいと思います。
動画
ドップラー効果の式
ドップラー効果の式は当然必要なものです。
今、振動数 $f$ の音を発しながら速さ $v_s$ で走る救急車があるとき、同じ直線上を走る自転車で観測される振動数を $f’$ とします。
また、$V :$ 音速、$v_o:$ 観測者(自転車)の速度 としましょう。
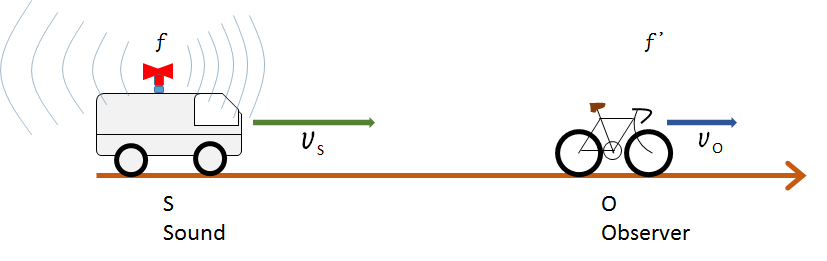
そうすると、
$$f’=f\times \dfrac{V-v_o}{V-v_s}$$
もちろん皆さん大丈夫ですね。
入試という限られた時間で問題を解くには、これくらいの式はスラスラと出てくる必要があります。
しかし、このドップラー効果の式を丸暗記しただけでは、ちょっとひねった問に対しては無力です。
考え方・導出方法が大事なのです。
波長を基準とした考え方
今回は今までと違う視点からドップラー効果についてアプローチします。
ぜひご参考に!
その方法とは、ズバリ波長 $\lambda$ をもとに考えます。
音源(救急車)から見る音の波長 $\lambda$ も観測者から見る波長 $\lambda$ も変化しません。
もし図のごとく音の波を見ることができたとして、救急車に乗っている人がものさしで測った波長も、自転車の人がものさしで測った波長も同じはずです。
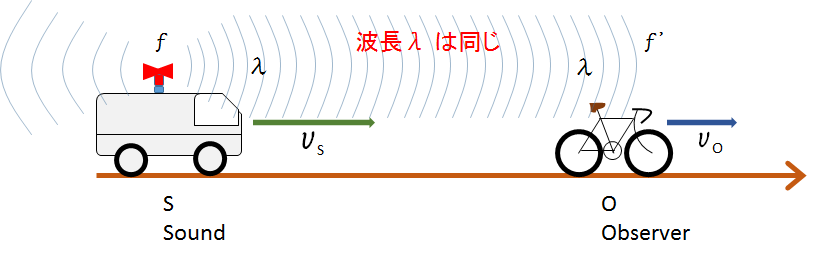
救急車の人は音の振動数は $f$ を聞いています。また、自転車の人は、$f’$ を聞いていますね。
そして、救急車の人の感じる音速は相対速度を考えて、$V-v_s$ 、
同様に自転車の人の感じる音速は $V-v_o$ です。
したがって、波長は $V=f\lambda$ より、$\lambda=\dfrac{V}{f}$ によって求めることができますから、
音源(救急車)から見る音の波長 $\lambda$ は、
$$ \lambda=\dfrac{V-v_s}{f} $$
そして、観測者から見る波長 $\lambda$ はこうなるはずです。
$$\lambda= \dfrac {V-v_o}{f’} $$
両者から見た波長 $\lambda$ は等しいため、
$$\lambda=\dfrac{V-v_s}{f}= \dfrac{V-v_o}{f’}$$
となります。
これは変形してやると、
$$f’=f\times \dfrac{V-v_o}{V-v_s}$$
となり、馴染みのある式になります。
波長は両者にとって共通であるということからドップラー効果の式が導けました。
最初に出てきたドップラー効果の式
$$f’=f\times \dfrac{V-v_o}{V-v_s}$$
を次のように変形すると波長 $\lambda$ が同じであることが導けます。
$$\lambda=\dfrac{V-v_s}{f}= \dfrac{V-v_o}{f’}$$





































コメント