物理のエッセンスの電磁気編コンデンサーの34番について解説します。
スイッチを入れたり切ったりした直後・・・というのはコンデンサーの問題ではよく見られるものです。
エッセンス コンデンサー34番 62ページ
問題概要
図の回路を考えます。ただし、最初の状態ではコンデンサーに電荷はありません。
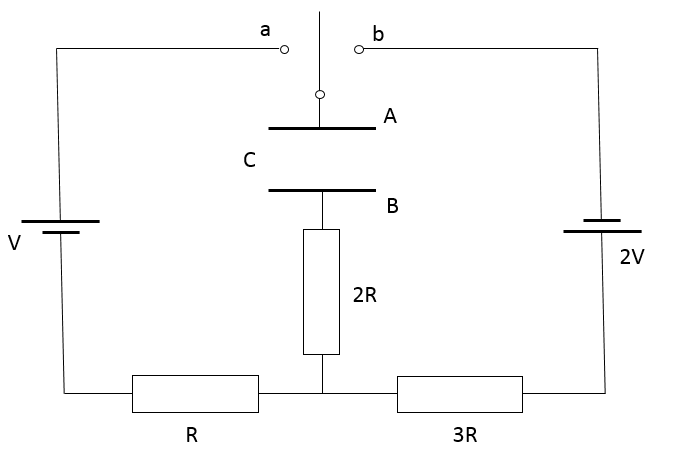
- スイッチを a 側に倒した直後の電流 $I_0$ を求めよ。
- 続いて十分時間が経過した後、スイッチを b 側に倒した直後の電流 $I_1$ を求めよ。
- $3R$ の抵抗を流れる総電気量を求めよ。
答え
動画で解説
1
スイッチを a 側に倒した直後、コンデンサーには電荷がないため、無抵抗の導線と考えてよいでしょう。これはよく使うので覚えておきましょう。
注意:あくまでも、直後だけの話です。
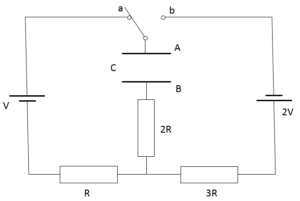
したがって、図の回路と等価です。
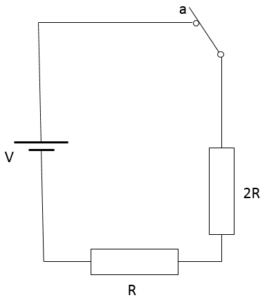
単純な抵抗の直列回路であるから、オームの法則 $V=RI$ より、
\begin{eqnarray}
I_0&=&\dfrac{V}{(R+2R)}\\\\
I_0&=&\dfrac{V}{3R}
\end{eqnarray}
2
1で十分に時間が経過したため、コンデンサーには電荷がたまっています。
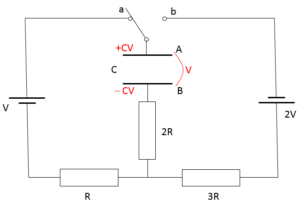
また、十分に時間が経過した後は、抵抗には電流が流れておらず、抵抗での電圧降下は $0$ になります。
そのため、スイッチを a 側に倒した後、十分に時間が経過すれば、コンデンサー両端の電圧は $V$ になっています。
つまり、スイッチを b 側に倒した直後は電圧 $V$ の電池として考えてよい。
したがって、図と等価と考えられます
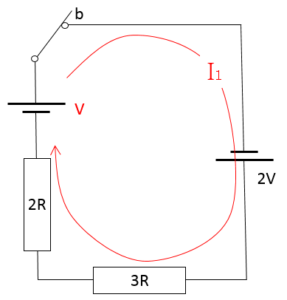
電流を図のように仮定すると、キルヒホッフの法則から
\begin{eqnarray}
(V+2V)&=&3RI_1+2RI_1\\
3V&=&5RI_1\\
I_1&=&\dfrac{3V}{5R}
\end{eqnarray}
$I_1$ は図の向きに流れます。
3
b 側にスイッチを接続した後、十分に時間がたったとき、回路は図のような状態であると考えられます。
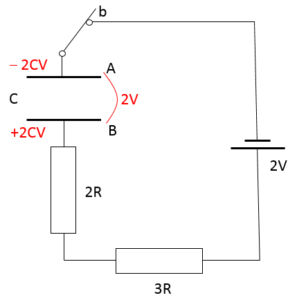
この単純な回路における電源は $2V$ だけです。
十分な時間が経過した後は回路に電流は流れてはいません。
そのため、各抵抗の電圧降下は $0$ となり、コンデンサーの極板間電圧は $2V$ となっているはずです。
よって、コンデンサーに溜まっている電荷は
$$Q=C(2V)=2CV$$
になっています。
$3R$ の抵抗を通る電荷については、スイッチを b 側に倒した以降だけを考えれば良いのです。
なぜならば、スイッチを a 側に倒した問題1の状態では抵抗 $3R$ には電流が流れていないからです。
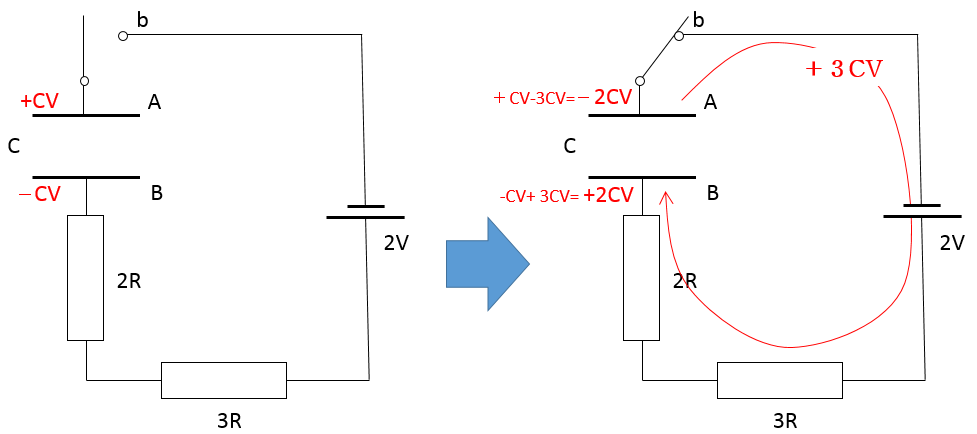
ここで、図におけるコンデンサーの下側の極板について考えれば、電荷は
$$-CV\:\rightarrow\:+2CV$$
と変化していることがわかります。
よって、
$$|+2CV-(-CV)|=3CV$$
の電気量が $3R$ の抵抗を通ったと考えられます。




































コメント