物理のエッセンス 熱力学 28番 P24
問題の概要
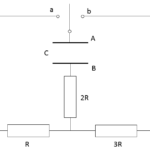
図のように、ピストンで2つの部屋 A、B に分けられたシリンダーがある。
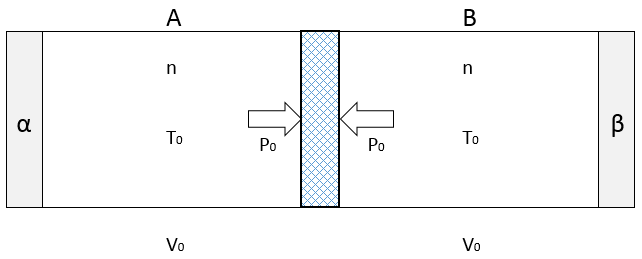
$\alpha$ 、$\beta$ は加熱器、冷却器である。また、ピストンや容器は断熱材でできている。
今、A、B内の気体のモル数は $n$、圧力は $P_0$、体積は $V_0$、温度 $T_0$ である。
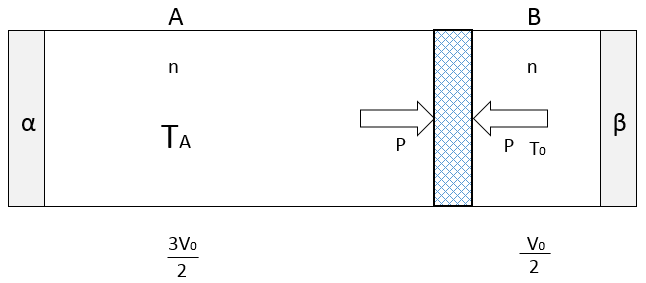
加熱器 $\alpha$ から気体 A に熱を与えるとピストンが移動し、A の体積は $\dfrac{3}{2}V_0$になった。
したがってB の体積は $\dfrac{1}{2}V_0$ となった。
ただし、B の気体の温度は操作中 $T_0$ で一定であった。
気体の定積モル比熱 $C_v$ とする。
- A 内の気体の内部エネルギーの変化分を求めよ。
- この装置において、$\alpha$ から $Q_1$ の熱を得たとする。
$\beta$ はどれだけの熱を奪ったか?$Q_2$ として答えよ。
答え
動画解説
1 A 内の気体の内部エネルギーの変化分を求めよ
内部エネルギーの変化分を $\Delta U$ とします。
この場合、定積モル比熱を用いて次のように示すことができます。
温度 $\Delta T$ 変化とする。
$$\Delta U=nC_v\Delta T$$
注意:ここで気体 A は定積変化ではないが、定積モル比熱は使っても差し支えありません。
詳しくは次を参照してください。

変化後の気体 A、B の圧力を $P$ とします。

ゆっくりと自在に動くピストンのため、A の気体の圧力とB の気体の圧力は変化の途中でも同じ値です。
ただし、この場合は定圧変化ではありません。
ここで、ボイル・シャルルの法則から
B の気体について、
$$\dfrac{P_0V_0}{T_0}=\dfrac{P\dfrac{1}{2}V_0}{T_0}$$
より、$P=2P_0$ です。
また、A の気体についてのボイル・シャルルの法則は、
$$\dfrac{P_0V_0}{T_0}=\dfrac{(2P_0)\dfrac{3}{2}V_0}{T_A}$$
ですね。
よって、$T_A=3T_0$ です。
ゆえに、$\Delta U=nC_v\Delta T$ より、
\begin{eqnarray}
\Delta U&=&nC_v\Delta T\\
&=&nC_v(3T_0-T_0)\\\\
\Delta U&=&2nC_vT_0
\end{eqnarray}
2 $\beta$ はどれだけの熱を奪ったか?
熱力学第1法則 $\:Q=\Delta U+W’$ ($W’$ は物体のした仕事)から、

この熱力学第1法則の式は2つの表現がありますので注意しましょう。
$\:Q=\Delta U+W’$ ($W’$ は物体のした仕事)
$\:\Delta U=Q+W$ ($W$ は物体がされる仕事)
A の気体のした仕事 $W’_A$ 、B の気体のした仕事 $W’_B$ とする。
1 より $\Delta U=2nC_vT_0$ だったから、
\begin{eqnarray}
Q_1&=&\Delta U+W’\\
&=&2nC_vT_0+W’_A
\end{eqnarray}
B の気体について考えると、物体から奪われた熱量を $Q_2$ とすると、
\begin{eqnarray}
-Q_2&=&\Delta U+W’_B\\
&=&nC_v(T_0-T_0)+W’_B\\
&=&0+W’_B
\end{eqnarray}

ここで、$-Q_2$ と、$Q_2$ にマイナスをつけるのはなぜですか?

熱力学第1法則をもう一度考えます。
物体の内部エネルギーの変化分 $\Delta U$ と、物体がした仕事 $W’$ の和は、物体に「与えた」熱量 $Q$ に等しい
$$Q=\Delta U +W’$$
です。
よって、基本的に $Q$ は「与えた」ものを正とすべきなのです。
ここでは「奪った」熱量を $Q_2$ としていますから、$-Q_2$ となります。
ややこしいですが・・・・。
個人的にはこういう設定はあまり好きではありませんね・・・。
ここで、A の気体のした仕事 $W’_A$ は 、-(B の気体のした仕事 $W’_B$ ) に等しいことから、
$$W’_A=-W’_B$$
です。

これは、A が膨張すると B が収縮するからですね。
B について、 $-Q_2=0+W’_B$ でしたから、
\begin{eqnarray}
Q_2&=&-W’_B\\
&=&W’_A\\
\end{eqnarray}
よって、$W’_A=Q_2$ だから、
\begin{eqnarray}
Q_1&=&2nC_vT_0+W’_A\\\\
Q_1&=&2nC_vT_0+Q_2
\end{eqnarray}
より、
$$Q_2=Q_1-2nC_vT_0$$
となります。
別解
装置全体を考えるとき、熱力学第1法則は成り立っているはずだから
$$Q=\Delta U + W’$$
が成立する。

熱力学第1法則を気体だけで成り立つの法則
だと思っていらっしゃる方がお見えかもしれませんが、
熱力学第1法則は
物体の内部エネルギーの変化分 $\Delta U$ と、物体がした仕事 $W’$ の和は、物体に「与えた」熱量 $Q$ に等しい
です。ここで「物体」としていることに注意してください。
つまり、熱力学第1法則とはすべての現象で成立するエネルギー保存の法則なのです。
気体の温度上昇は A と B で $2T_0$ だから、装置全体の内部エネルギー変化分は $\Delta U=2nC_vT_0$ となる。
また、与えられた熱量は、$Q=Q_1+(-Q_2)$
そして、全体では定積のため、気体のする仕事 $W’=0$ となり、
$$Q_1-Q_2=2nC_vT_0+0$$
ゆえに、
$$Q_2=Q_1-2nC_vT_0$$
Z会Asteria まずは無料でお試しください


































コメント