物理のエッセンス 熱力学 29番 P24
物理のエッセンス 熱・電磁気編の24ページ、29番の問題を参照してください。
やってみよう
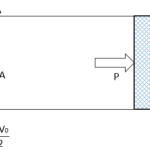
図のような装置を考える。最初の状態では、ばねは自然長である。
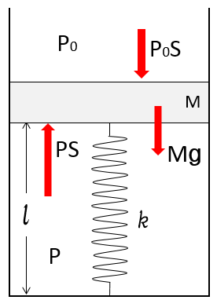
中の気体をあたためたら、気体が膨張し、ピストンは $h$ だけ上昇した。
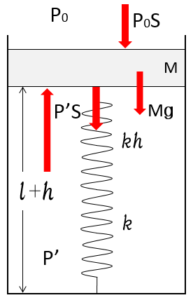
気体がした仕事を求める・・・・という問題です。

答え
このときの考え方ですが、気体のする仕事 $W=P\Delta V$ という式ではできません。
なぜかというと、この仕事の式 $W=P\Delta V$ は、圧力が一定であるという条件でしか使えないからです。
この場合は、圧力一定である次の $P-V$ 図において四角形の面積を求めていることになります。
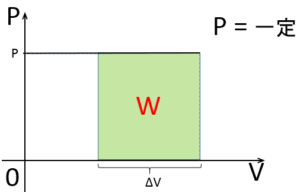
この問題では、ばねが伸びるにつれピストンを引く力がだんだん大きくなりますから、気体の圧力はだんだん大きくなっていきます。
グラフを使って
ただし、圧力が変化する場合でも、$P-V$ 図を用いれば仕事を求めることができる場合もあります。
つまり、$P-V$ 図においてグラフと $V$ 軸の囲む面積を求めることで仕事を求めるわけです。
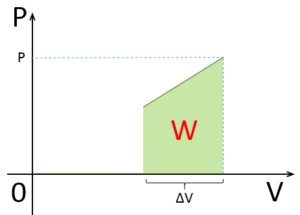
図では、台形の面積を求めることで仕事を求めることができます。
さて、この29番の問題では、圧力はどのように変化するかを考えてみましょう。
最初の状態での圧力 $P$ は、

ピストンにはたらく力のつり合いを考えて、
$$PS=P_0S+Mg$$
です。よって、圧力は
$$P=P_0+\dfrac{Mg}{S}$$
です。
ピストンが $x$ だけ上昇しているときの圧力 $P_x$ は、
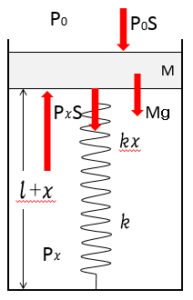
図より、ピストンにはたらく力のつり合いを考えて、
$$P_xS=P_0S+Mg+kx$$
です。よって、気体の圧力は、
$$P_x=P_0+\dfrac{Mg}{S}+\dfrac{k}{S}x$$
より、$P_x=ax+b$ と書くことができます。
($a=\dfrac{k}{s},\:\:\: b=P_0+\dfrac{Mg}{S} $ で、ともに定数)
このとき、断面積が一定のため、気体の体積 $V$ は $x$ に単純比例して大きくなっていきます。
すなわち, $P_x$ は、$P-V$ 図においても直線となることがわかります。

$V=S(l+x)$ から、$x=\dfrac{V}{S}-l$ を代入しても明らかです。
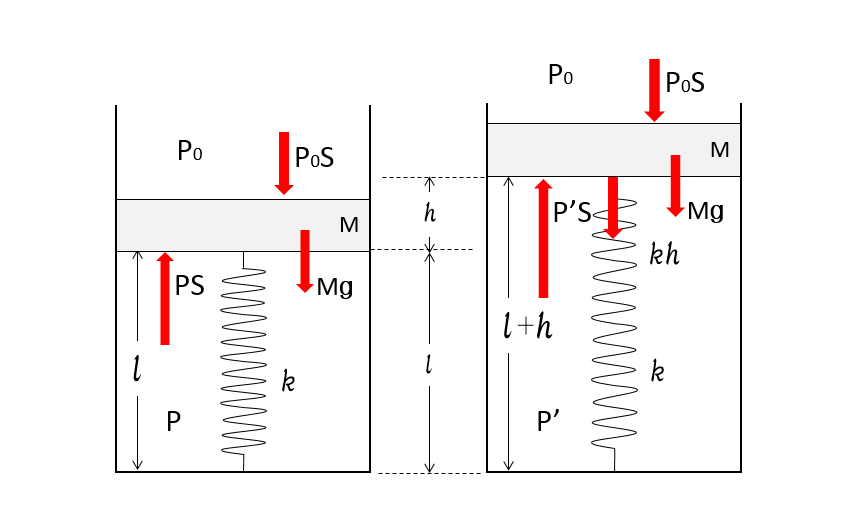
今、$h$ だけ上昇しているわけですから、その時の気体圧力 $P’$ は、
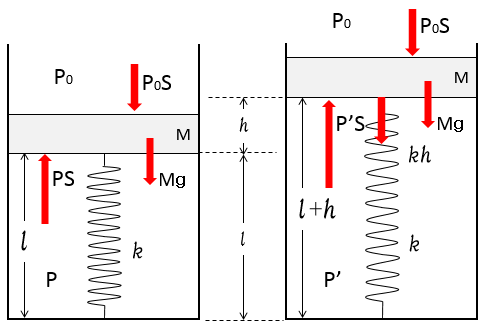
図より、
$$P’S=P_0S+Mg+kh$$
よって、
$$P’=P_0+\dfrac{Mg}{S}+\dfrac{k}{S}h$$
$P=P_0+\dfrac{Mg}{S}$ でしたから、これを使うと、
\begin{eqnarray}
P’&=&P_0+\dfrac{Mg}{S}+\dfrac{k}{S}h\\\\
&=&P+\dfrac{k}{S}h
\end{eqnarray}
そして、体積は、$P\;\rightarrow\:Sl$、$P’\;\rightarrow\:S(l+h)$ です。
よって図のようになります。
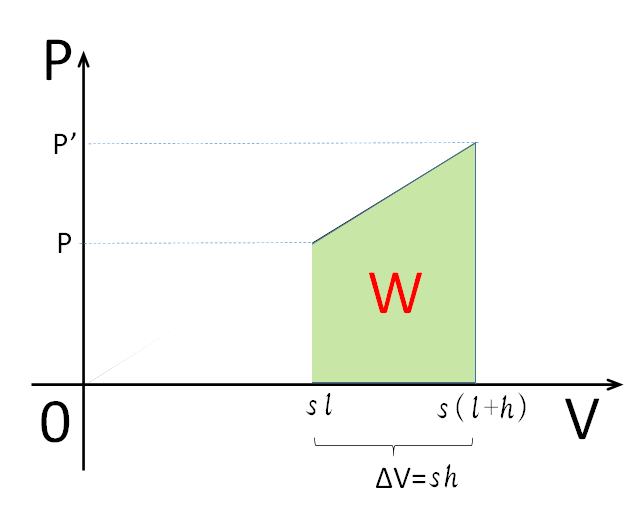
ということは、この問題における $P-V$ 図のグラフと $V$ 軸の囲む面積を求めればよいのです。
図の台形面積を求めるとそれが答えの仕事量 $W$ です。$\left(P=P_0+\dfrac{Mg}{S}\right)$
\begin{eqnarray}
W&=&\dfrac{P+P’}{2}Sh\\\\
&=&\dfrac{P+P+\frac{k}{S}h}{2}Sh\\\\
&=&\left(2P_0+\dfrac{2Mg}{S}+\dfrac{kh}{S}\right)\dfrac{Sh}{2}\\\\
&=&\left(P_0S+Mg+\dfrac{kh}{2}\right)h
\end{eqnarray}
となります。
積分してみると
ちなみに、
$$P_x=P_0+\dfrac{Mg}{S}+\dfrac{k}{S}x$$
を積分しても答えを得ることができますね。
$$W=\int^{S(l+h)}_{Sl} P_x dV$$
ただし、$V=S(l+x)$ より、$x=\dfrac{V}{S}-l$ です。
あるいは、$dV=Sdx$ だから、
$$W=\int^{h}_{0} P_x Sdx$$
としてもよいでしょう。こちらのほうが計算がラクです。
エネルギーで 1
エネルギーの関係から考えます。
ピストンを考えるとき、大気圧に接していて、ゆっくりとなめらかに動いたわけですから、
ピストンへの(重力・ばねの力)と(内部の気体圧力による力)の合力は、大気圧による力 $P_0S$ に等しいはずです。
したがって、このときピストンが大気圧に対してした仕事は $P_0Sh$ となります。
しかし気体は膨張して仕事をし、それはピストンの位置エネルギーとばねのエネルギーにも変わっています。
よってエネルギー的には、$Mgh+\dfrac{1}{2}kh^2$ も気体のした仕事になります。
つまり、気体のした仕事は
$$W=P_0Sh+Mgh+\dfrac{1}{2}kh^2$$
となります。
エネルギーで 2
装置全体のエネルギーから考えてみましょう。
(最初のエネルギー)+仕事=(最後のエネルギー) の関係から
$$E_0+W=E$$
装置全体では、$Q$ の熱エネルギーを吸収して、$h$ だけ膨張しています。
ピストンを考えるとき、大気圧に接していて、ゆっくりとなめらかに動いたわけですから、
ピストンへの(重力・ばねの力)と(内部の気体圧力による力)の合力は、大気圧による力 $P_0S$ に等しいはずです。
したがって装置は、大気に対して $P_0Sh$ の仕事をしています。
つまり装置としては、これだけのエネルギーを失っていると考えられます。
ここでは位置のエネルギーを考えて、装置の持つエネルギーを、
(重力の位置エネルギー+ばねの位置エネルギー+気体の内部エネルギー) とします。
気体の内部エネルギーをそれぞれ、$U_0$、$U_1$ 、重力の位置エネルギー基準をシリンダーの底とすると、
$$(Mgl+0+U_0)+(-P_0S\times h+Q)=\{Mg(l+h)+\dfrac{1}{2}kh^2+U_1\}$$
ここで、熱力学第1法則から、$Q=\Delta U+W$ ($W$ は気体のした仕事)ですから、
$$(Mgl+U_0)+(-P_0S h+\Delta U+W)=\{Mg(l+h)+\dfrac{1}{2}kh^2+U_1\}$$
$$(Mgl)+(-P_0Sh+\Delta U+W)=\{Mg(l+h)+\dfrac{1}{2}kh^2+(U_1-U_0)\}$$
ここで、$\Delta U=U_1-U_0$ だから、
$$(Mgl)+(-P_0Sh+\Delta U+W)=\{Mg(l+h)+\dfrac{1}{2}kh^2+\Delta U\}$$
$$(Mgl)+(-P_0Sh+W)=\{Mg(l+h)+\dfrac{1}{2}kh^2\}$$
$$W=Mgh+P_0Sh+\dfrac{1}{2}kh^2$$




































コメント