熱力学第1法則
熱力学の第一法則には次の2つの表現があります。
- 「物体に外部から与えた熱量 $Q$ と、外部から加えた仕事 $W$ は、内部エネルギーの増加 $\Delta U$ に等しい」
すなわち、$\Delta U＝Q＋W$ と示される。
あるいは
- 「物体に外部から与えた熱量 $Q$ は、気体が外部にした仕事 $W’$と、内部エネルギーの増加 $\Delta U$ の和等しい」
こちらは、$Q＝\Delta U＋W’$ となります。
ただし、気体がされる仕事 $W$ と、気体がする仕事 $W’$ は、$W=-W’$ の関係があります。
このブログではこちらの式 $Q＝\Delta U＋W’$ を主に使うことにします。
また、これらの法則は、エネルギー保存則を示しています。
すべてのエネルギーは、いろいろその姿を変えるが、その総量は増えも減りもしないのです。
それでは、以下では気体のいろいろな変化について解説していきます。
熱力学第2法則についてはこちらへ
定積変化
体積 $V$ を一定に保つ変化です。
簡単にいうと、缶詰みたいな容器に入れた気体を温めたり、冷やしたりする場合をイメージしてください。
この場合は、気体のする仕事 $W’$ は $0$ です。
なぜなら、定積のため、$W’=p\Delta V$ において、$\Delta V=0$ だからです。
熱力学第1法則の式は、$W’=0$ より、
$Q＝\Delta U＋W’=\Delta U$
$p-V$ 図は、体積が一定であるため、図のように $p$ 軸に平行な直線となります。
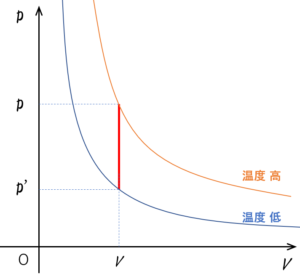
定圧変化
圧力 $p$ を一定に保つ変化です。
簡単に言うと、ピストンの自由に動く注射器のようなものへ、気体を入れたとイメージしてください。
熱力学第1法則の式は、$W’=p\Delta V$ より、
$Q＝\Delta U＋W’=\Delta U+p\Delta V$
$p-V$ 図は、圧力が一定であるため、図のように $V$ 軸に平行な直線となります。
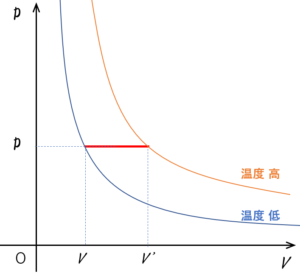
等温変化
温度 $T$ が一定の変化です。定積モル比熱を $C_V$ とすると、
$\Delta U=nC_V\Delta T=0$ となります。
熱力学第1法則の式は、
$Q＝\Delta U＋W’=0+W’ $
$Q=W’$
$p-V$ 図は、温度が一定であるため、図のように $pV=一定$ のグラフになります。
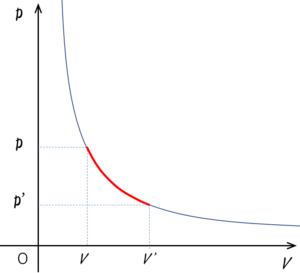
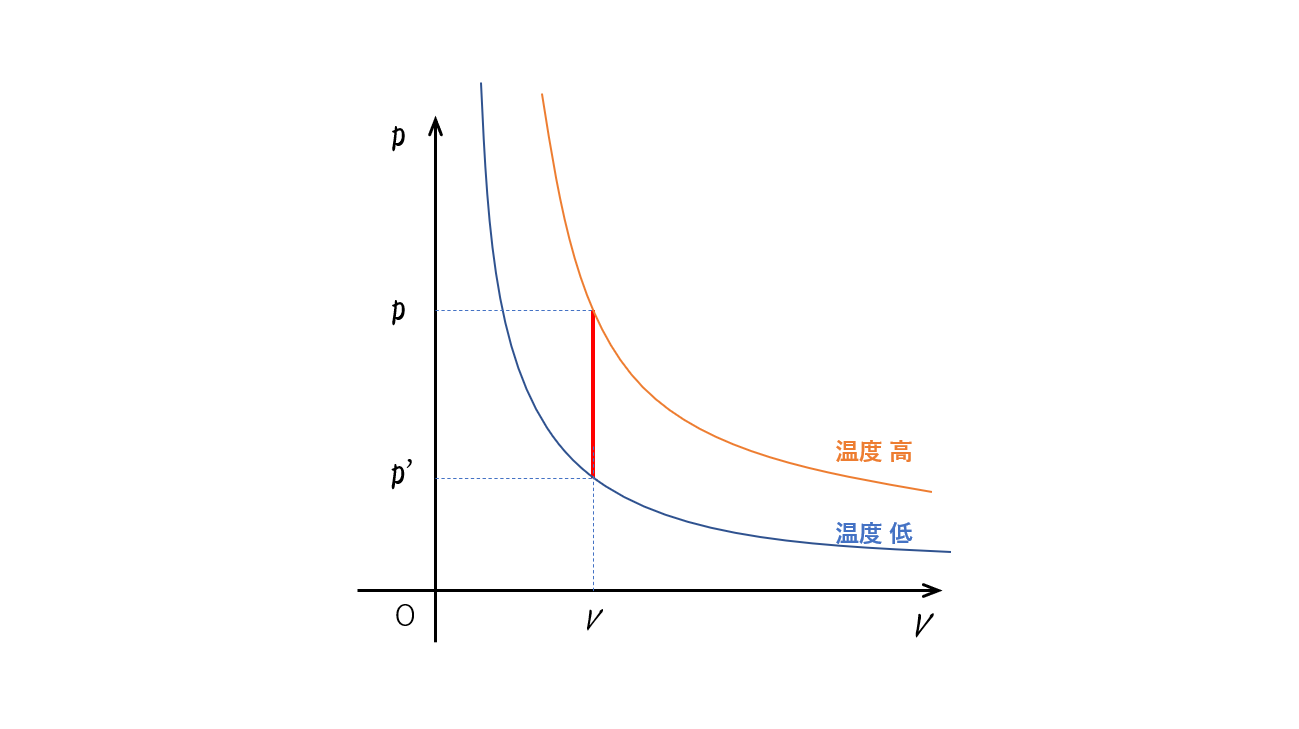
等温変化のグラフから、$p-V$ 図の、次の性質をよく理解しておきましょう。
図より、グラフの右上に行くほど気体温度が上がっていることがわかります。
この性質は等温変化のときだけではなく、すべての場合に言えます。
断熱変化
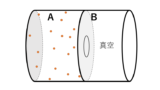
断熱変化とは外部との熱の出入りがない変化です。
例えば、真空の保温ポットに気体を入れて、中だけで変化するようなイメージです。
熱の出入りがないので $Q=0$ です。
熱力学第1法則の式は、
$Q＝\Delta U＋W’ $
$0=\Delta U+W’$
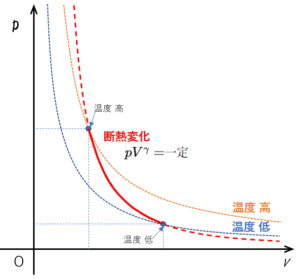
準静的変化の時、ポアソンの法則にしたがうため、 $p-V$ 図は、$pV^{\gamma}=一定$ に従います。
ただし、$\gamma=\dfrac{C_p}{C_V}$ です。定圧モル比熱： $C_p$ 、定積モル比熱： $C_V$
コメント