物理のエッセンス力学編 1番
加速度グラフ
$v-t$ 図から加速度グラフを描きます。
(a) のグラフ
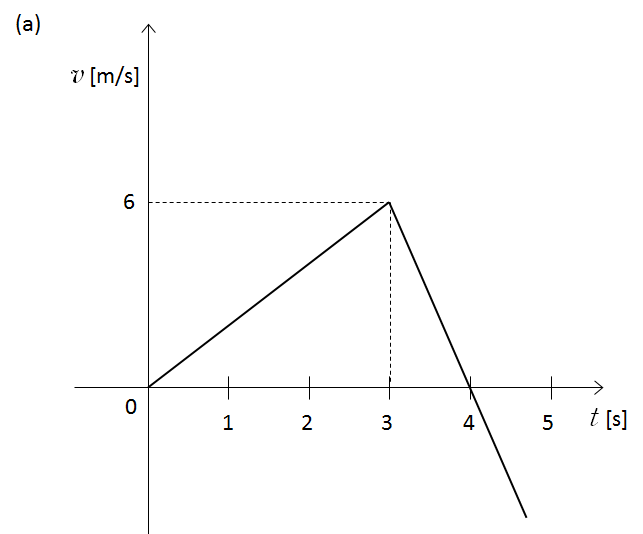
加速度 $a$ は、 $a=\dfrac{\Delta v}{ \Delta t}=\dfrac{v’-v}{t’-t}$ で示されます。
0 ~ 3 [s] ・・・ $a=\dfrac{6-0}{3-0}=2\:[\mathrm{m/s^2}]$
3 ~ 4 [s] ・・・ $a=\dfrac{0-6}{4-3}=-6\:[\mathrm{m/s^2}]$
答え
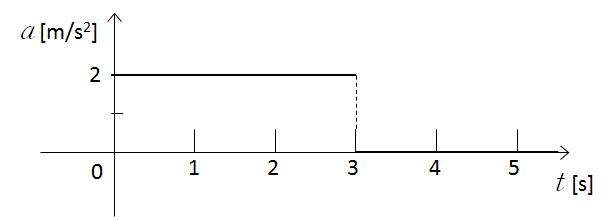
したがって、加速度グラフは次のようになります。
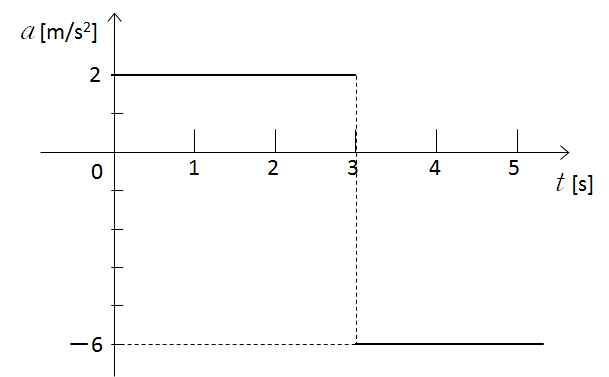

0 ~ 3 [s] 間、3 [s] 以降では加速度はそれぞれ一定です。
それは $v-t$ グラフの傾き(加速度)が一定であることからわかります。

加速度が一定なので $a-t$ グラフの傾きは 0 です。
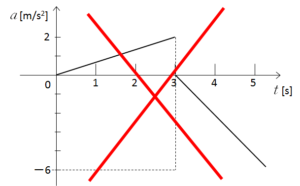
グラフを斜めにしてはいけません。
(b) のグラフ
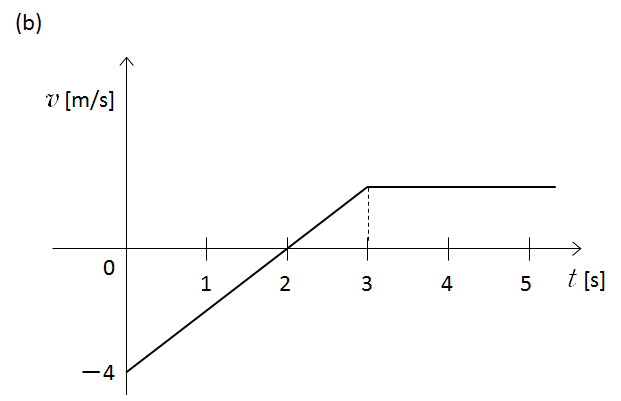
加速度は $v-t$ グラフの傾きなので、前半の 0 ~ 3 [s] 間の加速度(グラフの傾き)は一定です。したがって、加速度(グラフの傾き)は、求めやすい 0 ~ 2 [s] 間で計算します。
後半の 3 [s] 以後のグラフの傾きは 0 なので、加速度も 0 です。
0 ~ 3 [s] ・・・ $a=\dfrac{0-(-4)}{2-0}=2\:[\mathrm{m/s^2}]$
3 ~ 4 [s] ・・・ $a=\dfrac{0}{4-3}=0\:[\mathrm{m/s^2}]$
答え
加速度グラフは次図

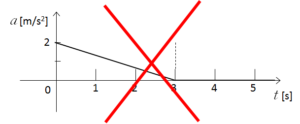
0 ~ 3 [s] 間、3 [s] 以降では加速度はそれぞれ一定です。
それは $v-t$ グラフの傾き(加速度)が一定であることからわかります。

加速度が一定なので $a-t$ グラフの傾きは 0 です。
グラフを斜めにしてはいけませんよ。
走行距離
$v-t$ 図で 4 [s] 間の走行距離について考えます。
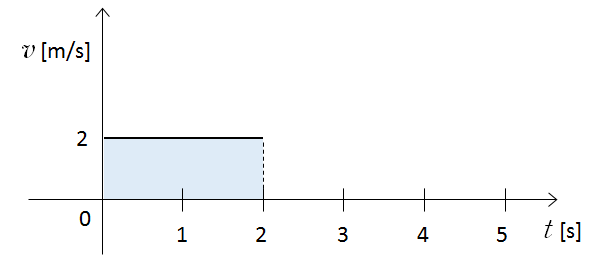
一般的に等速運動の場合は、 $x=vt$ ですから、例えば次の $v-t$ 図において、次の図の青色で囲まれた面積が走行距離 $x$ を示しています。 距離 = $x$ = 2 × 2 = 4 [m]
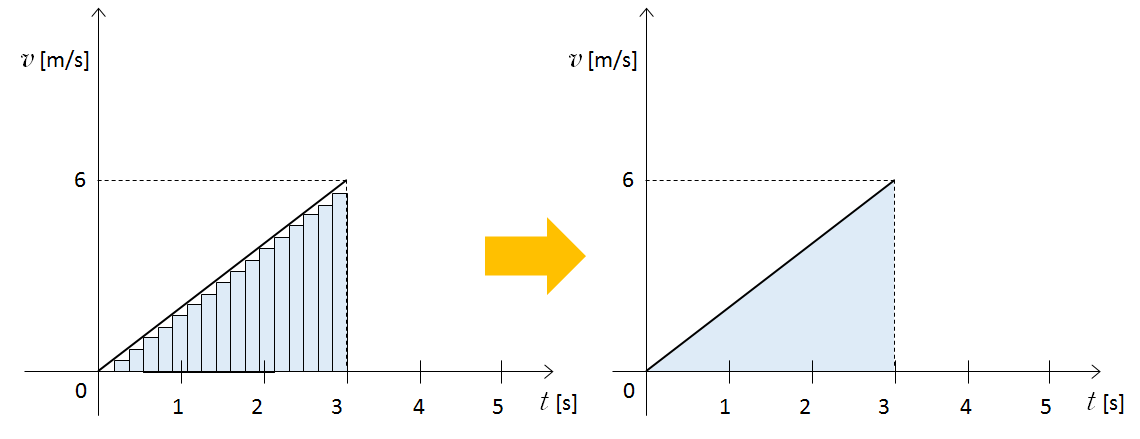
もし、等速運動ではない場合、次の図のように長方形をたくさん考えます。
このとき、長方形を限りなく細くしてやれば、その面積の総計で走行距離(この場合は図の三角形の面積)を求めることができます。これは積分の考え方ですね。
では問題の各グラフについて考えていきましょう。

(a) のグラフ
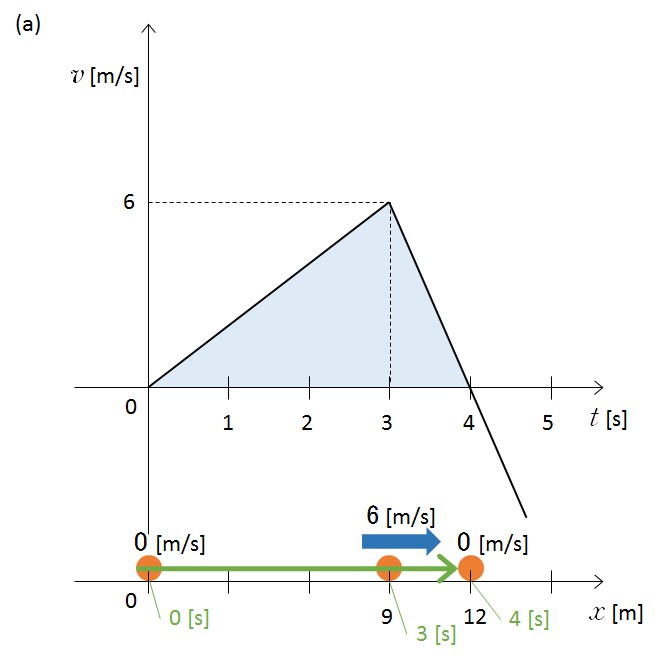
0 ~ 4 [s] の走行距離・・・ 三角形の面積 = 底辺 × 高さ ÷ 2 = 4 × 6 ÷ 2 = 12 [m] となります。
答え 12 [m]
(b) のグラフ
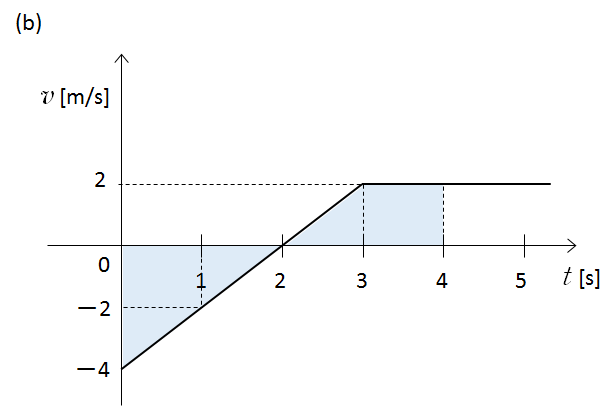
0 ~ 2 [s]
0 ~ 2 [s] 間は $v$ は 負の値ですが、走った距離は 速さ×時間 ですから、絶対値を取り、
0 ~ 2 [s] の走行距離・・・ 三角形の面積 = 底辺 × 高さ ÷ 2 = 2 × |-4| ÷ 2 = 4 [m]
となります。どの方向へ走ろうが、走った距離は方向とは無関係であるからですね。
2 ~ 3 [s]
次に 2 ~ 3 [s] 間ですが、傾き(加速度)が 2 のため、3 [s] での 速さ $v$ は 2 [m/s] です。
2 ~ 3 [s] の走行距離・・・ 三角形の面積 = 底辺 × 高さ ÷ 2 = 1 × 2 ÷ 2 = 1 [m]
3 ~ 4 [s]
3 ~ 4 [s] の走行距離・・・ 四角形の面積 = 1 × 2 = 2 [m]
以上より、0 ~ 4 [s] 間の走行距離は、 4 + 1 + 2 = 7 [m] となります。
答え 7 [m]
ちなみに、右向きを正とした変位 $x$ と時間・速さを示した図は次のようになります。
最初に $x$ の負の方向へ運動していることに注意します。
もとの位置に戻る時間
もとの位置に戻る時間を考える前に、変位についておさらいしておきましょう。
変位について
記事 変位とは にあるように変位は始点と終点を結んだベクトルで示されます。したがって方向性を持ちます。
変位は、一直線上の運動であるなら平面の場合と違って、単純な足し算引き算でベクトルを計算することができます。
(a) のグラフ
グラフより、最初に $x$ の正方向へ運動を始め、3 [s] で最高速度に達し、その後減速して 4 [s] 後に速度 0 になります。
4 [s] 後の変位量は、正方向に 12 [m] です。
$t$ 軸より上で計算される面積が正の変位、下の面積が負の変位となります。
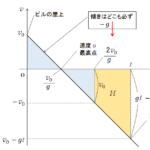
したがって、元の位置( $x=0$ )に戻る時間は、次の図のオレンジの色の三角形が青色の三角形と同じ面積になればよいことになります。
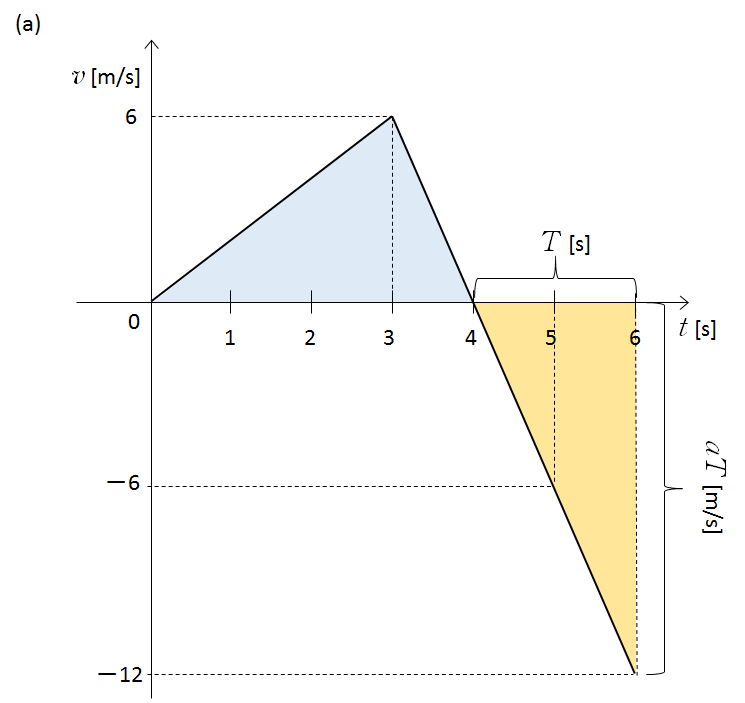
3 [s] 以降の加速度は $-6\:[\mathrm{m/s^2}]$ ですから、 4 [s] 以降 $T$ [s] でオレンジの三角形の面積が 12 [m] になるとすれば、$T$ [s] 後の速さ(速度の大きさ)は $|v|=|at|=|aT|$ だから、
$\mathrm{三角形の面積}=\dfrac{\mathrm{底辺} \times \mathrm{高さ}}{2} = \dfrac{T \times |aT|}{2}=12$
3 [s] 以降の加速度の大きさは $|a| = |-6|\:[\mathrm{m/s^2}]$ だから、
$\dfrac{T\times 6T}{2}=12$
よって、$T=2\:[\mathrm{s}]$
最初からの時間は、 $4+2=6\:[\mathrm{s}]$ となります。
答え $6\:[\mathrm{s}]$
違う方法を考えて見ましょう。
グラフをもとに、この物体の運動と変位・時刻・速度をイメージ図にしたのが次の図です。
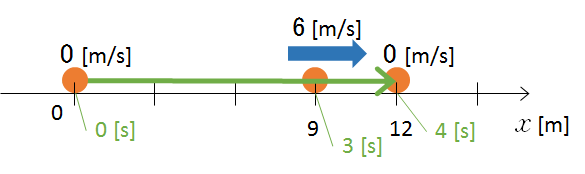
今、 時刻 4 [s] で最右端に来ており、その速度は 0 です。
元の位置( $x=0$ )に戻るためには、12 [m] バックすればよいことになります。
時刻 4 [s] での物体の加速度の大きさは $|-6|\:[\mathrm{m/s^2}]$ ですから所要時間を $t$ とし、 $x=v_0t + \dfrac{1}{2}at^2$ より、12 [m] を加速度 $6\:[\mathrm{m/s^2}]$ で図の左向きに進むと考えて、
$12=0\times t + \dfrac{1}{2}6t^2$
とすると、 $t=2\:[\mathrm{s}]$ であることがわかります。
よって、スタートからの所要時間は、 $4+2=6\:[\mathrm{s}]$
答え $6\:[\mathrm{s}]$
(b) のグラフ
グラフより、最初 $x$ の負方向へ -4 [m/s] で運動し、2 [s] 後に速度 0 。その後、正方向へと速度が変化し 3 [s] 後に最高速度になって以降は等速直線運動します。
$t$ 軸より上で計算される面積が正の変位、下の面積が負の変位となります。
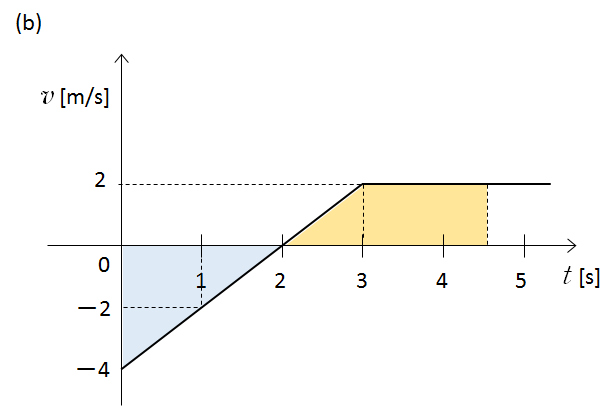
下の青色の三角形面積は $\dfrac{2\times |-4|}{2}=4 \:[\mathrm{s}]$
したがって、元の位置( $x=0$ )に戻る時間は 4 [m] だけ引き返すことを考えて、上図のオレンジの色の図形の面積が青色の三角形と同じ面積になればよいことになります。
2 ~ 4 [s] 間のオレンジの図形の面積は、 3 [m] ですから、あと 1 [m] ですね。速さは 2 [m/s] ですからあと 0.5 [s] かかることがわかります。
よって答えは 4.5 [s] 後になります。
答え 4.5 [s]
ちょっと違う方法を考えて見ます。
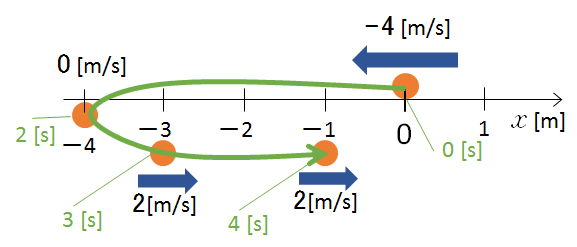
グラフをもとに、この物体の運動と変位・時刻・速度をイメージ図にしたのが次の図です。
最初、原点から負の方向(図の左)へ進んでいることに注意してください。
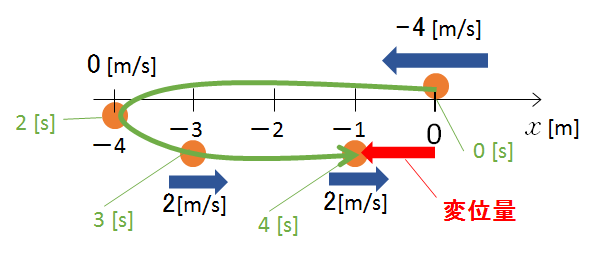
このときの変位は、図の赤いベクトルで示したものであり、この場合は ー1 [m] となります。
これから明らかなように、元の位置( $x=0$ )に戻るまで残り 1 [m] です。
また、3 [s] 以降は正の方向へ速度 2 [m/s] の等速直線運動をしているため、あと $t=1\:[\mathrm{m}]\div 2\;[\mathrm{m/s}] =0.5\:[\mathrm{s}]$ だけ等速直線運動すればよいことがわかります。
したがってスタートからの経過時間は $4+0.5=4.5\:[\mathrm{s}]$ となります。
答え 4.5 [s]





































コメント
[…] 物理のエッセンス力学編 1番 物理のエッセンス力学編 1番 加速度グラフ $v-t$ […]