物理のエッセンス力学編15番
良くある相対速度の問題です。
ただし一直線上ではなく、平面での場合です。
後半では相対速度ベクトルの図がなぜ成立するかについても解説しています。
問題
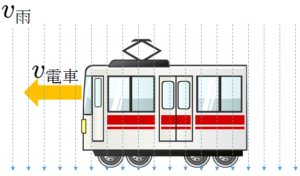
今、雨が鉛直に 10 m/s で降っている。
水平に等速直線運動する列車から雨を見ると、雨は鉛直線から 30° 傾いて降っているように見えた。列車の速さ $v$ を求めよ。
という内容です。
相対速度
大事なことなので、相対速度についてもう一度おさらいをしておきましょう。
解説
ここではわかりやすくするため、電車の速度を $v_{\mathrm{電車}}$ 、雨の速度を $v_{\mathrm{雨}}$ 、電車から見た雨の速度を $v_{\mathrm{電車} \rightarrow \mathrm{雨}}$ とします。
ここで「電車から見た雨の速度」 $v_{\mathrm{電車} \rightarrow \mathrm{雨}}$ は相対速度です。
$v_{\mathrm{電車} \rightarrow \mathrm{雨}}=v_{\mathrm{雨}} \:- v_{\mathrm{電車}} $
です。これは一直線上ではなく、平面的なベクトルになるので、次の図のような関係です。
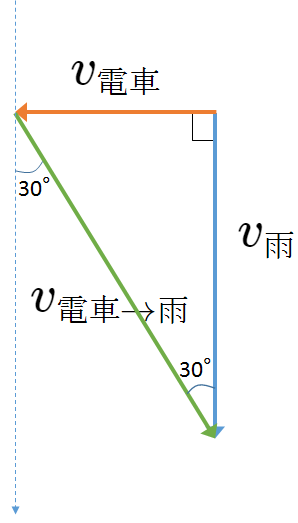
これは「相対速度のうまい方法」で解説したように、地面に対する2つのベクトル「電車の速度」 $v_{\mathrm{電車}}$ 、「雨の速度」 $v_{\mathrm{雨}}$ の始点を合わせて、ベクトルの矢印の先の「見るほう」から「見られるほう」へベクトルを引けば得られます。
このときの「見るほう」から「見られるほう」へ引いたベクトルが「電車から見た雨の速度」 $v_{\mathrm{電車} \rightarrow \mathrm{雨}}$ となるのです。
したがって、$\tan$ を使って
$\tan 30^\circ = \dfrac{v_{\mathrm{電車}}}{v_{\mathrm{雨}}}$
$v_{\mathrm{電車}}={v_{\mathrm{雨}}}\tan 30^\circ $
$~~~~~=\dfrac{10}{\sqrt{3}}$
$~~~~~ \fallingdotseq 5.8 \: [\mathrm{m/s}]$
しかし、なぜこのようなベクトルを描けばいいのでしょうか。次ではそのことについて考えて見ます。
相対速度ベクトル
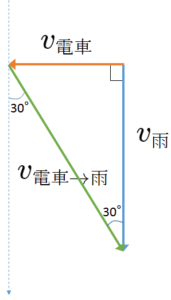
相対速度ベクトルは図を描くことができれば簡単です。
でもなぜ図のようなベクトル図を描いて相対速度ベクトルを求められるのでしょうか。
$v_{\mathrm{電車} \rightarrow \mathrm{雨}}=v_{\mathrm{雨}} \:- v_{\mathrm{電車}} $
ここでは、雨粒の1つに注目して考えて見ます。
ある瞬間に雨粒1つに注目して電車内の同じ位置から写真を撮ったとします。
これがその写真だとしましょう。
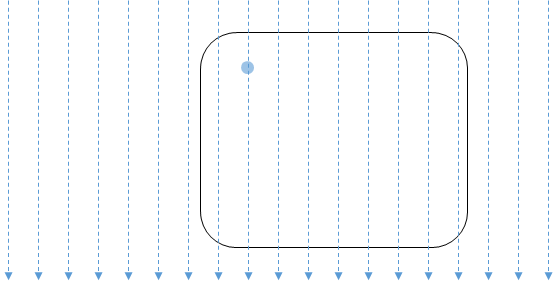
ではちょうど1秒後にもう一度、電車内から写真を撮ります。
もしも、電車が駅に停車しているなら雨は鉛直にきっちり 10 m だけ落ちているはずです。
その写真が次の図です。
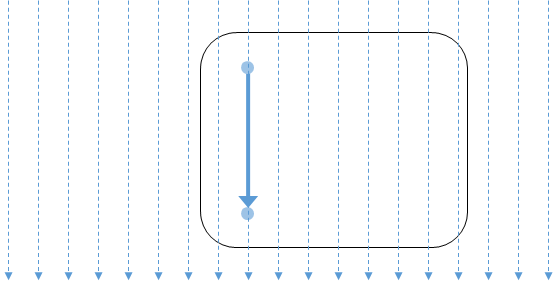
しかし、電車が水平に等速直線運動している場合、同じ1秒で電車は進行方向に $v_{\mathrm{電車}}$ だけ進んでいるはずですから、そのときに動く電車内から撮った写真は次の図のようになっているはずです。
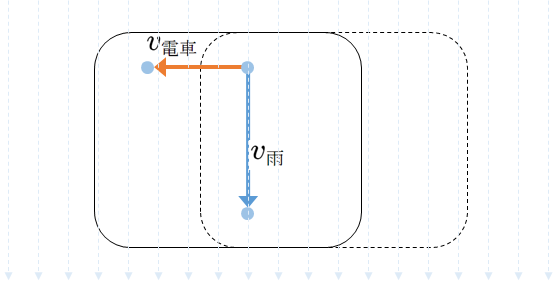
写った写真だけを見れば(・・・つまり、電車内の人から見れば → 相対速度 のことですね )結局、雨粒の写真は次の図の緑の矢印の運動をしたと見えるわけです。
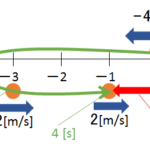
なので、静止系から見た各物体の速度ベクトルの始点を合わせ、見るほうから見られるほうへ矢印を引いてベクトルを描けば、それが相対速度ベクトルになります。
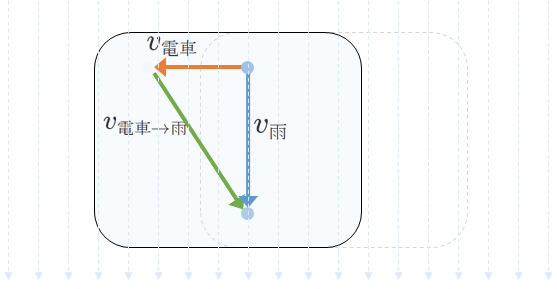




































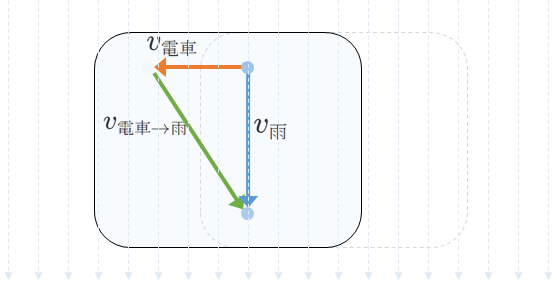

コメント