問題自体は難しくはありません。
ここでは、解説に載っているのとは異なる方法($v-t$ グラフを用いる方法)でといてみます。
物理のエッセンス力学編5番
問題概要
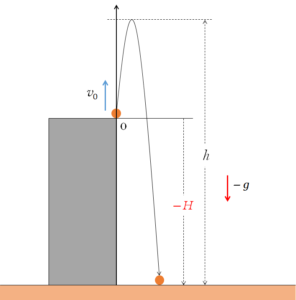
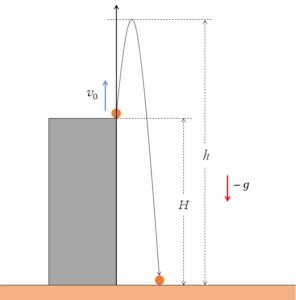
高さ $H$ のビルの屋上から鉛直上方に初速 $v_0$ でボールを投げるとき、
- 地面からの最高点高さ $h$
- 地面に落ちるまでの所要時間
を求めます。
最高到達点
まず、地面からのボールの最高到達点の高さ $h$ ですが、$v-t$ グラフを考えてみます。
ここでは鉛直上方を正に取っています。
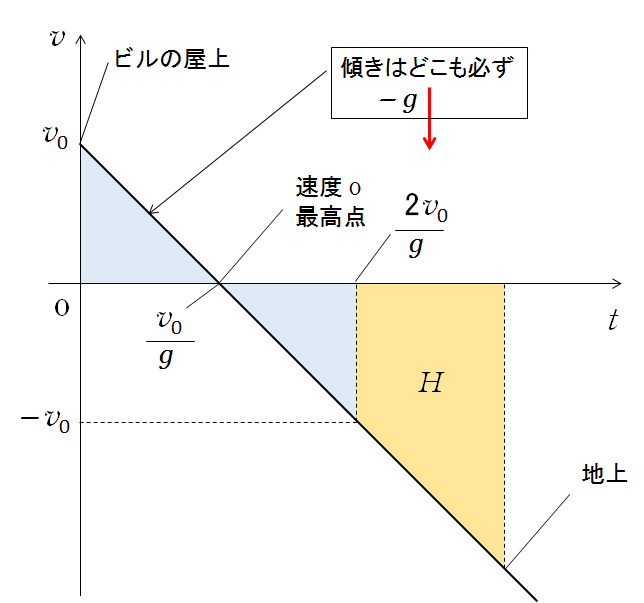
このとき、初速度は鉛直上方に $v_0$ です。そして徐々に速さを失い、最高到達点では速度 0 になります。
その後、負の方向に速さを増していきます。
- ここで大事なこと・・・この $v-t$ グラフの傾きは必ず $-g$ です( 傾きの大きさ $g$ )。
このあたりのことは v-t グラフの活用 反発問題のテクニック解説 を参照してください。

空気などの抵抗がないとき、
投げ上げようが投げ下ろしをしようが水平投射だろうが斜方投射だろうが、
鉛直方向の加速度の大きさは重力加速度 $g$ 以外にはありえません。
なぜって?
抵抗がなければ、どのような運動でも物体には鉛直下方にだけ $mg$ がかかるからです。
運動方程式 $ma=F$ より、 $ma=mg$ したがって、$a=g$ (鉛直下方)
ただし、正方向の取りかたで、その正負は変わります。

重力だけによる運動(抵抗がない場合)では鉛直方向の
$v-t$ グラフの傾きの大きさは常に $g$ で同じです。
では最高点までの時間はどうなるのでしょうか?
ここで ・・・「公式」に当てはめる(私のキライなフレーズです)・・・ のではなく、グラフから考察します。
グラフの傾きの大きさは $g$ 以外にありえない!・・・ のでした。
そうすると図の最高点(速度 0)の時刻 $t$ は傾きを求める式、 $\dfrac{\mathrm{高さ}}{\mathrm{底辺}} = \dfrac{v_0}{t}=g$ からカンタンにわかります。
すなわち、 最高点に到達するまでの時間は $t=\dfrac{v_0}{g}$ です。
そうすると最高点のビルの屋上からの高さは図の水色の三角形の面積に等しく、
$\mathrm{ビルの屋上から最高点まで} = \dfrac{v_0}{g}\times v_0 \times \dfrac{1}{2}=\dfrac{v^2_0}{2g}$
地上からの高さ $h$ は $H$ を足せばよいことから
$h=\dfrac{v^2_0}{2g} + H$
となります。
答え $h= H + \dfrac{v^2_0}{2g} $
ついでに・・・

図の水色の三角形二つは合同であることが自明です。
なぜって? その三角形の面積は移動距離を表していますから、ボールを投げ上げた後、ビルの屋上にボールが戻ったときは変位 0 だからです。
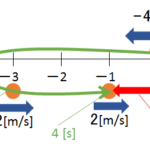
ゆえに、ボールを投げ上げた後、ビルの屋上にボールがもどる時刻は
$2\times \dfrac{v_0}{g}$ ですね。
そしてそのときの速度は、計算せずとも三角形の合同性から $-v_0$ です。
地面に到達するまでの時間
地面に到達する時刻を $t$ とします。
そうすると落下の式から、そのときの速度 $v$ は $v=v_0\: -\: gt < 0 $ です。
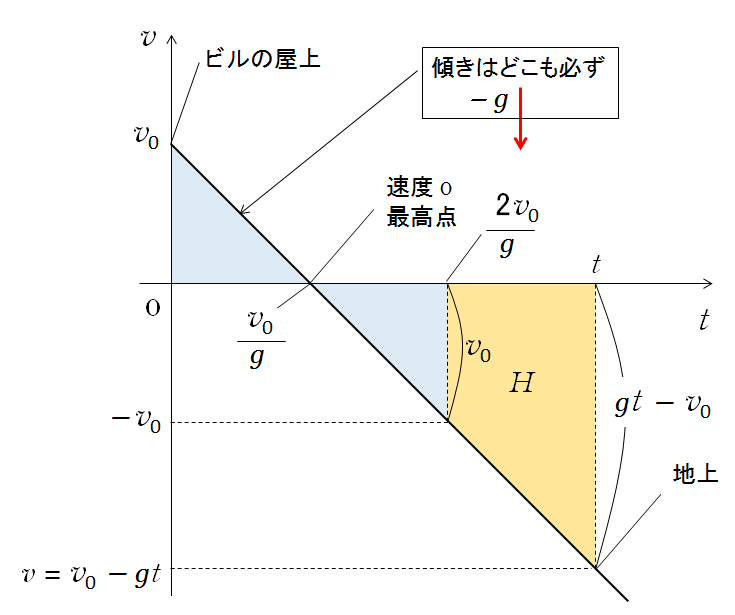
図のオレンジの台形の面積がビルの高さ $H$ のはずですから、
台形の上底の長さは $v_0$ 、 $v_0-gt < 0 $ であることに注意すると、下底の長さは $(gt-v_0)$ であるから、
台形の面積 = (上底 + 下底 )× 高さ ÷ 2 より
$H=\{v_0 + (g t – v_0 )\} \times \left (t \:-\: \dfrac{2v_0}{g} \right )\times \dfrac{1}{2}$
より、
$gt^2-2v_0 t-2H=0$
この $t$ に関する2次方程式を解の公式を用いて、
$t=\dfrac{1}{g}\left ( v_0 \pm \sqrt{v^2_0 + 2gH} \right)$
ただし、$t>0$ に注意して、
答え $t=\dfrac{1}{g}\left ( v_0 + \sqrt{v^2_0 + 2gH} \right)$

ただし、こちらは、 $y=v_0t – \dfrac{1}{2}gt^2$ から
$-H=v_0t – \dfrac{1}{2}gt^2$
としたほうがすっきり・カンタンですね・・・
ビルの屋上を原点としているため、地面は $-H$ となることに注意してください。




































コメント