合成ばね定数については一度は目を通しておきましょう。
知らないと手間取るかもしれません。
物理のエッセンス力学編23番
合成ばね定数
合成ばね定数を求める問題です。
合成ばね定数については以下で解説しています。
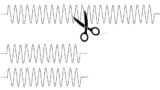
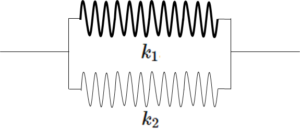
- 並列の合成ばね定数 $k_r$ の求め方・・・$k_r=k_1+k_2$
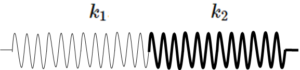
- 直列の合成ばね定数 $k_r$ の求め方・・・$\dfrac{1}{k_r}=\dfrac{1}{k_1}+\dfrac{1}{k_2}$

これってどこかで見ましたね。
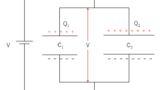
コンデンサーの並列の合成容量の求め方と同じです。
(合成抵抗の求め方とは直列並列の式が逆になっています)
解説
(a)
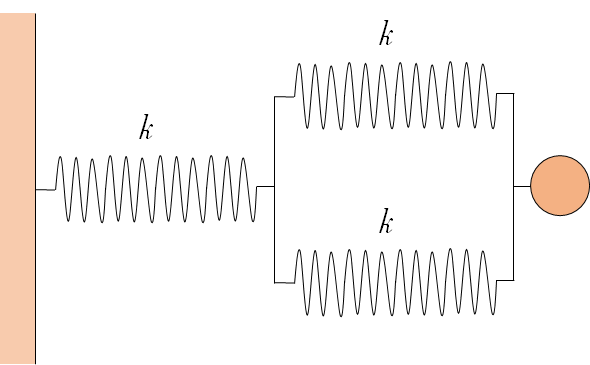
並列と直列が混在しています。
まず、並列部分の合成ばね定数 $k’_r $ をもとめると $k_r=k_1+k_2$ より、
$k’_r=k+k=2k$
そうすると、次の図のようにかけます。
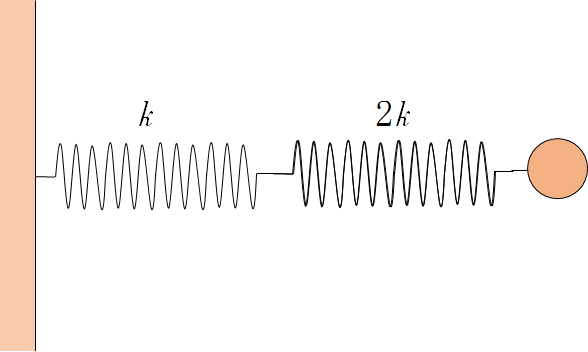
今度は、$k$ と $2k$ のばねの直列ですから、全体の合成ばね定数 $k_r$ は、
$\dfrac{1}{k_r}=\dfrac{1}{k}+\dfrac{1}{2k}$
より、
$k_r=\dfrac{2}{3}k$
(b)
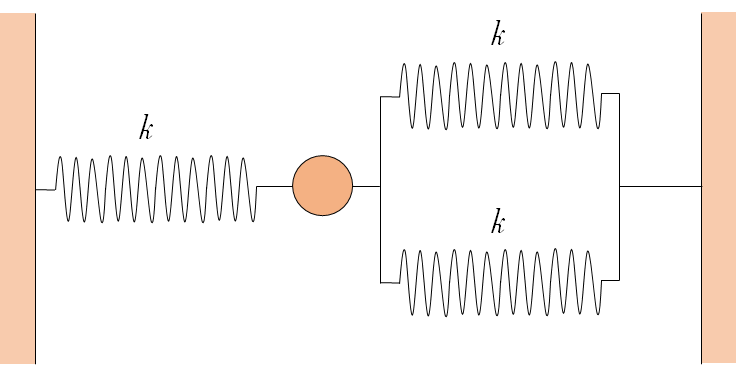
これも並列と直列が混在しています。
同じように並列部分を合成してみると、その合成ばね定数 $k’_r$ は、 $k_r=k_1+k_2$ より、
$k’_r=k+k=2k$
次に残りの部分を考えます。
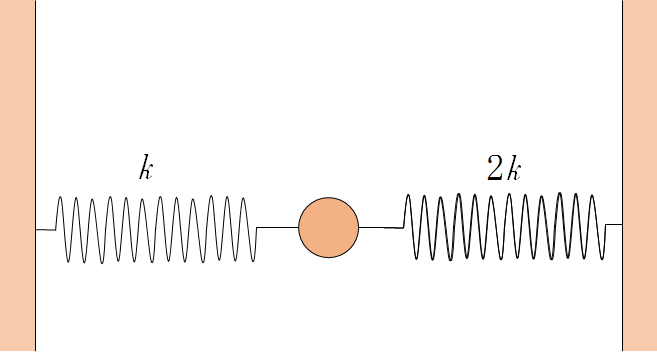
ここで注意してほしいのはこのばねは両端が壁に固定されているということです。
つまり、左側のばねが伸びるとき、右側のばねは同じ量だけ縮むことになります。
したがって、(a) の場合とは少し違います。
今、左側のばねを $x$ 伸ばしたとします。そうすると、右側のばねは $x$ だけ縮みます。

(a) の直列のばねは、
どちらのばねも伸びるところが違いますね。
左側のばねはもとの長さに戻ろうと $kx$ の力を左方向に及ぼします。
同様に右側のばねは、$2kx$ の力をやはり左方向に及ぼします。
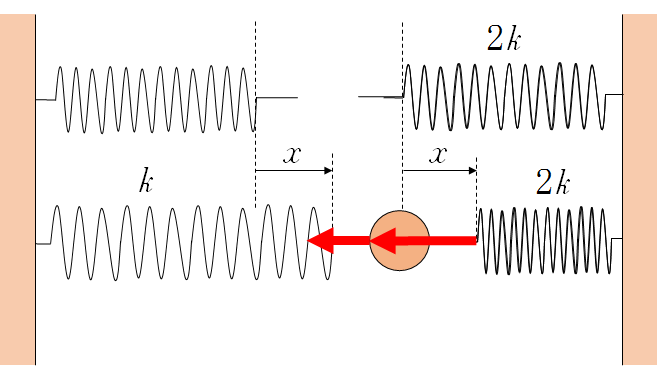
すなわち、合力 $kx+2kx=3kx$ となるため、ばね定数並列のときと同じく、単純に足せばよいことがわかります。
したがって、
$k_r=k+2k=3k$
合成ばね定数については以下で解説しています。
なぜ直列と並列の式がでてくるのか・・・・など詳しく解説しています。





































コメント