合成ばね定数をもとめる式を理解しましょう。
たとえ忘れてもすぐに作ることができます。
物理のエッセンス力学編24番
問題概要
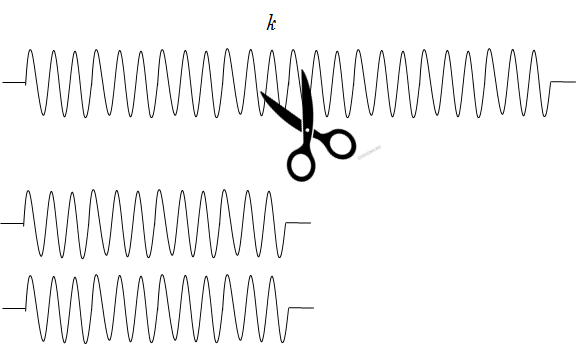
ばね定数 $k$ のばねを半分に切ります。
次に、その切ったばねを並列つなぎにします。
このとき、ばね定数はいくつになるでしょうか。
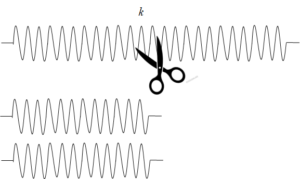
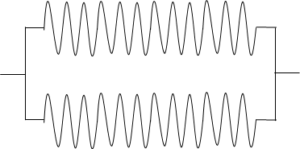
解説
ばねを短くするとばねはかたくなります。
これは直感に反するかもしれません。
しかし、ばねを伸ばすことを考えてみます。
ばねを小さなばねをつなぎ合わせたものとしてイメージします。
半分に切ったばねを、切る前と同じだけ伸ばすためには、ばねを構成する小さなばねは、切る前よりもより長く伸びる必要があります。
したがって短く切るとばねは固くなるのです。
具体的なばね定数の計算
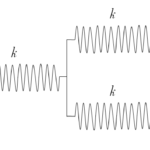
- 並列つなぎのときの合成ばね定数 $k_r$ は、 $k_r=k_1+k_2$
- 直列つなぎのときの合成ばね定数 $k_r$ は、 $\dfrac{1}{k_r}=\dfrac{1}{k_1}+\dfrac{1}{k_2}$
このあたりのことは、 物理ワンポイント 合成ばね定数の求め方 を見てください。
詳しく解説しています。
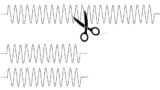
物理ワンポイント 合成ばね定数の求め方
ばねを切ったりつないだりした場合のばね定数はどのようになるでしょうか。
これを知っていると、いろいろなところで役立ちます。
kokolainen.com
上の式から具体的には半分に切った場合、ばね定数は2倍になります。（$\frac{1}{3}$ の場合は3倍です）
よって、このばね定数 $k$ を半分に切ったばねのばね定数は $2k$ です。
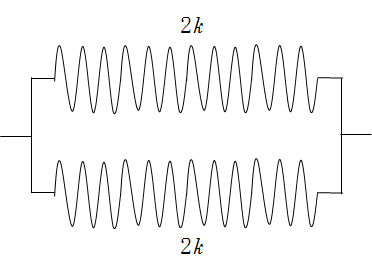
このばねを並列つなぎするのですから、並列した場合のばね定数 $k_r$ は、 $k_r=2k+2k=4k$ となります。
答え $4k$
合成ばね定数の求め方
合成ばね定数の求め方については以下のリンクを見てください。
物理ワンポイント 合成ばね定数の求め方
ばねを切ったりつないだりした場合のばね定数はどのようになるでしょうか。
これを知っていると、いろいろなところで役立ちます。
kokolainen.com
合成ばね定数の式を丸暗記するのではなく、理解してイメージを作りましょう。
そうすれば、たとえ式を忘れてもすぐ作ることができます。
そして応用がききます！！！
コメント