これも $v-t$ グラフを用いてやってみましょう。
物理のエッセンス力学編6番
問題概要
高さ $H$ のビルの屋上から物体を水平投射する。このとき、最初に地面に衝突するまでの水平到達距離 $x$ を求めよ。 重力加速度 $g$ とし、空気抵抗は無視できる。
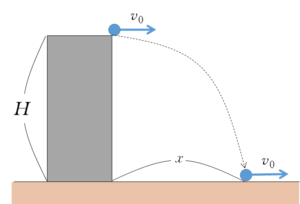
解説
水平投射です。鉛直方向と水平方向に分けて考えます。
鉛直方向
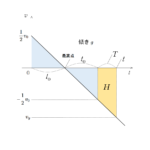
$v-t$ グラフを描いてみます。
鉛直方向には初速度 0 ですので、自由落下します。
鉛直下向きを正としてみました。
この $v-t$ グラフの傾きは $g$ です。
そうすると、グラフの傾きが $g$ であるから、地面に到達する直前の鉛直方向の速さを $v_y$ とすると、
$\mathrm{グラフの傾き}=g=\dfrac{v_y}{t}$
$v_y=gt$
となります。

そして、グラフが $t$ 軸と囲む三角形面積が、ビルの高さ $H$ を示しています。
これらのことから、物体が投げ出されて以後、地面に到達するまでにかかる時間 $t$ がわかります。
$\mathrm{三角形の面積}=H=\dfrac{1}{2}\times t\times (gt)$
$t=\sqrt{\dfrac{2H}{g}}$
水平方向
水平方向には等速運動しますから、水平方向の速さ $v_x=v_0$ で、その距離 $x$ は
$x=v_x t=v_0 t$
ここで、 $t=\sqrt{\dfrac{2H}{g}}$ だから、
$x=v_0\sqrt{\dfrac{2H}{g}}$
答え $x=v_0\sqrt{\dfrac{2H}{g}}$

計算式を使うのも大切ですが、・・・「公式」を丸暗記してあてはめる(私のキライなフレーズです)・・・してはいけません。




































コメント