物理のクイズ　走行距離を計算せよ

単純な物理のクイズです。

走行距離を計算せよ

問題

図にあるように、自動車が一直線上を運動するとします。
A 地点を初速度 0 で出発した後、ある一定の加速度で運動して時速 $36\: \mathrm{km/h}$まで加速。
その直後、加速時とは異なる大きさの一定の加速度で減速し、B 地点で停止。
停止時に時計を見ると出発からちょうど 1 時間が経過していましたとさ。

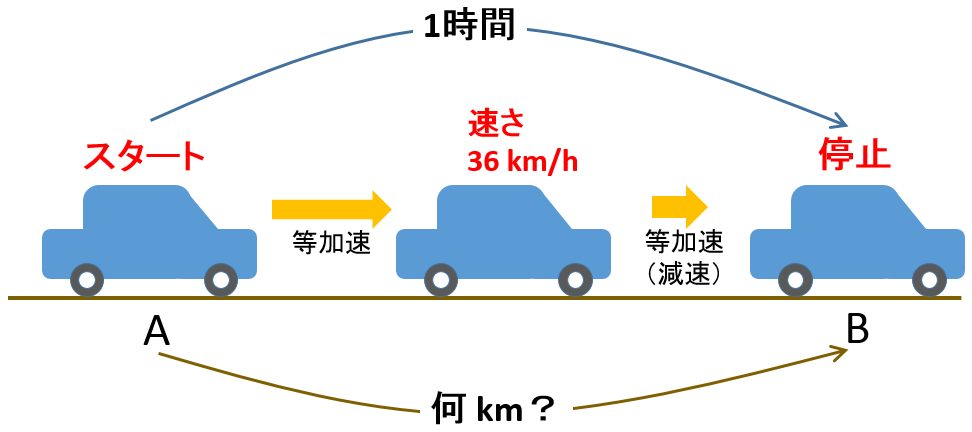
さて、この自動車は出発してから停止するまでに何 $\mathrm{km}$ 走行したでしょうか？

考えてみましょう。

解答

答えは、$18\:\mathrm{km}$ です。
この場合、加速度の大きさがどのような値でも距離はいつも同じく $18\:\mathrm{km}$ になります。

なぜでしょうか？
$v-t$ グラフを書いてみれば一目瞭然です。
え？加速度不明のため描けないって？
でも要は走行距離がわかれば良いので、とにかくイメージでも良いので描いてみましょう。

加速時と減速時の加速度の大きさが不明ですが、ともに等加速度運動をしたのがポイントです。

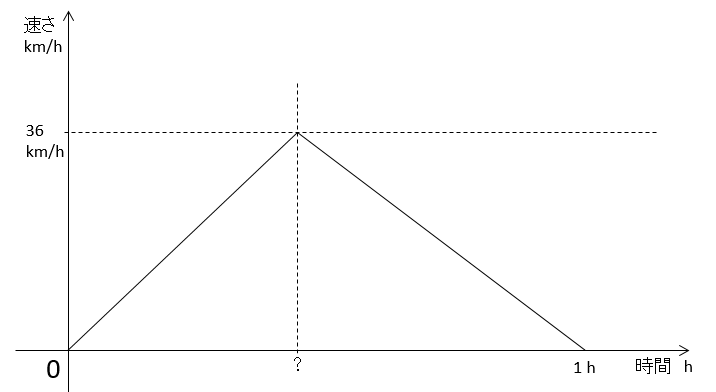
一般に、$v-t$ グラフにおいては等加速直線運動のグラフの傾きは一定です。
そのため、この問題のグラフも必ず直線で構成されます。

この問題の場合、初速度 0 でスタートしてから時速 $36\:\mathrm{km/h}$ まで等加速直線運動しています。
そして、$36\:\mathrm{km/h}$ に達した瞬間から等加速度で減速して停止します。

ゆえに、加速度はわからずとも、グラフは図のように三角形になるはずです。

このときの自動車の走行距離は、$v-t$ グラフと時間軸が囲む面積で示されます。

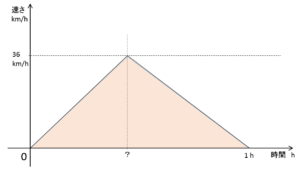
つまり、図の三角形の面積（色のついた部分）が求める走行距離です。
しかしこのグラフは数ある運動の中の単なる一例にしか過ぎませんね。

ここでもう一度確認しておきましょう。
この問題のグラフにおいて守るべきことは、グラフが直線で構成されることと最高速度が $36\:\mathrm{km/h}$ であること、停止まで 1 時間だということです。

この約束に従えば、次の図にあるように緑や赤の点線で示された三角形も当然考えられます。

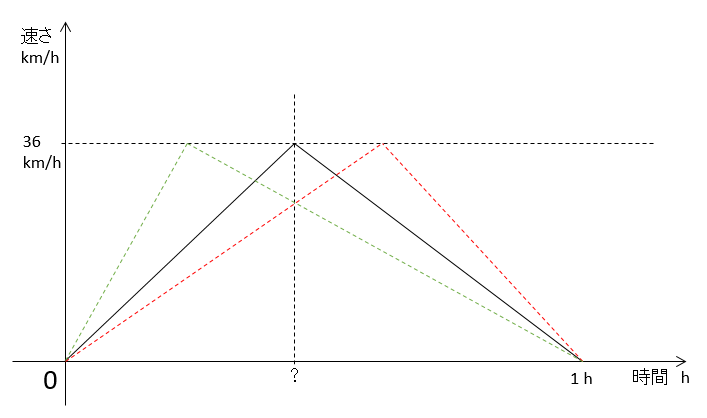
ここまでくればもうおわかりだと思いますが、これらの三角形の面積はどれも同じです。
なぜなら、三角形の面積はすべて、面積＝底辺×高さ÷2　から計算できるからですね。
すなわち三角形面積は、

$面積＝底辺\times 高さ\div 2=1\times 36\div 2=18$

となるので自動車の走行距離は、グラフの三角形の形にかかわらずいつも $18\:\mathrm{km}$ となります。

まとめ

以上を計算式でやろうとすると結構な労力が必要ですね。
物理においては、ときとしてグラフが強力なパワーを発揮します。
グラフを考えることで問題を簡単に解決できる、あるいは糸口がつかめる場合も数多くあります。

いままでやってきた問題についても一度グラフを考えてみるのもいいと思います。
これからグラフの活用方法についても順次紹介していきますね。

おすすめの問題集・参考書です。

Amazon Amazon