
AnnaliseArt / Pixabay
角運動量って何でしょうか?
運動量は知っているけど、角がつくとわからない・・・
でも、フィギィアスケートのスピンで回転数が増すのが角運動量保存則だと聞いた人も多いかもしれませんね。
定義を聞いてもいまひとつピンときません。
ここでは、その角運動量保存則を納得できる形で説明します。
角運動量保存則
ニュートンのプリンキピアは科学史における名著です。ニュートンはこの書物の中であえて数式を排して幾何学的方法により自己の理論の主張を行っています。
ここででは、天体の運行に対するニュートンの記述を見ながら角運動量保存則について考えてみたいと思います。
面積速度一定の法則
まず太陽の周りの楕円軌道を惑星が運行していると考えます。
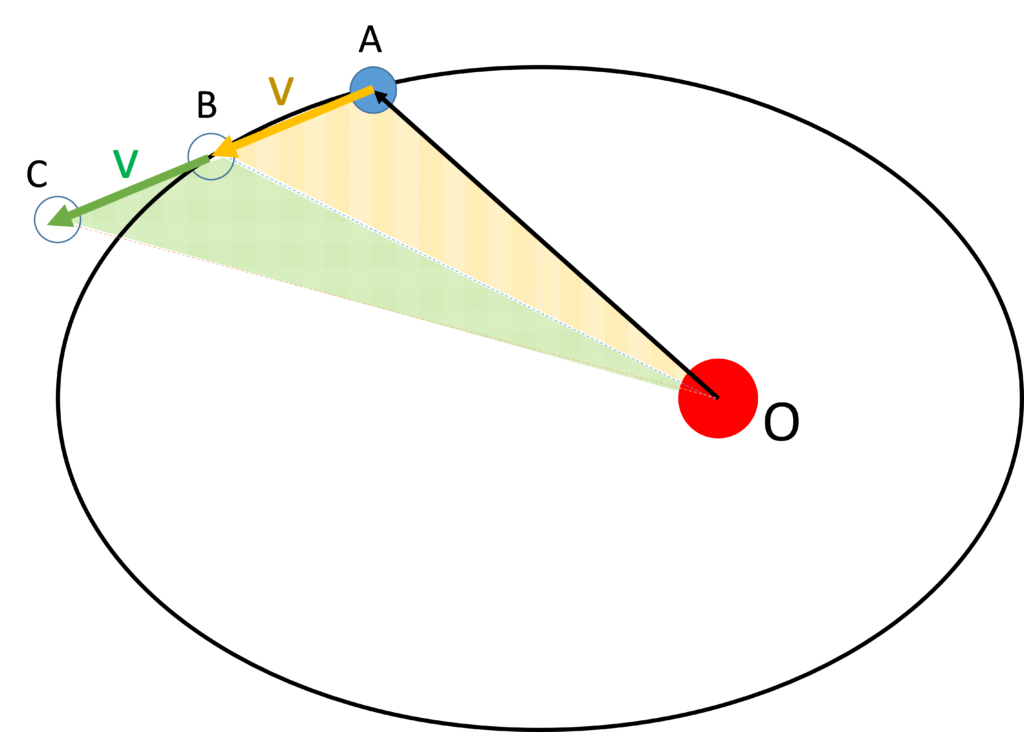
このとき、回転中心は楕円の二つある焦点の片方であることはケプラーによりすでに明らかにされていました。
ここでは速さ $v$ で微小時間運動したと仮定します。B 地点を通過した惑星は万有引力がなければ慣性の法則により直進して C の位置に到達するでしょう。
そのとき、等速のためAB = BCですから、三角形OABと三角形OBCは面積が等しくなるはずです。
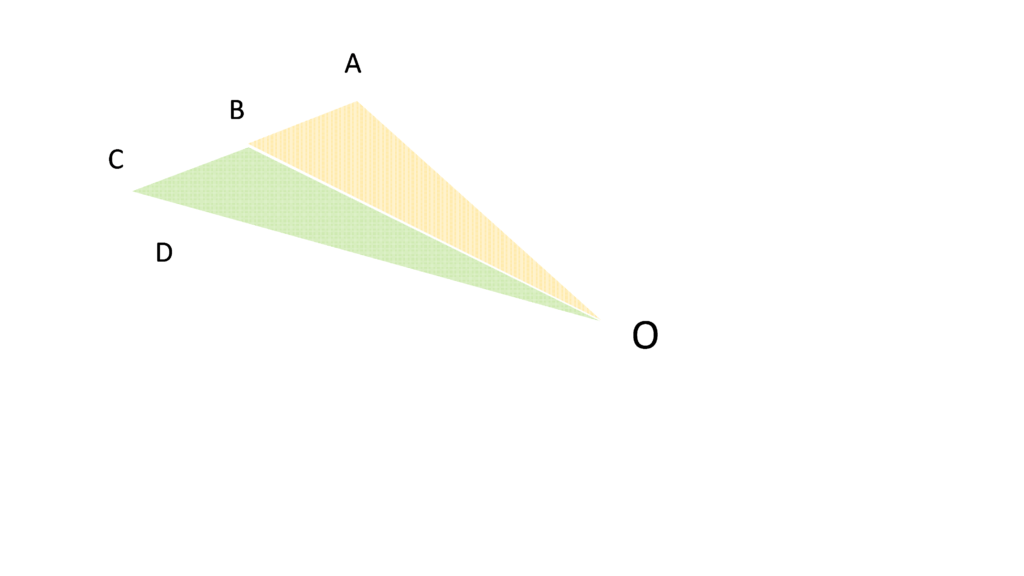
しかし、実際は万有引力により、次の図のようにA ⇒ B ⇒ D と方向が変わります。
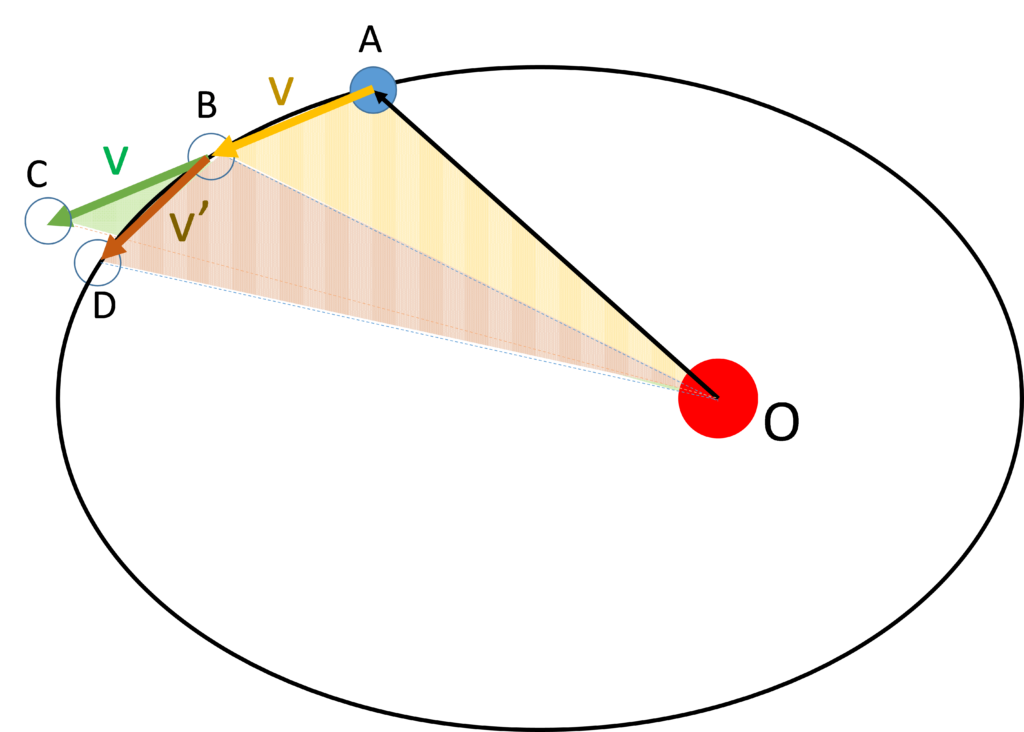
三角形OBCと三角形OBD について考えます。
ニュートン運動方程式より $ ma = F $ ですが、この意味するところは $ F $ の方向と $ a $ の方向が必ず一致するということです。
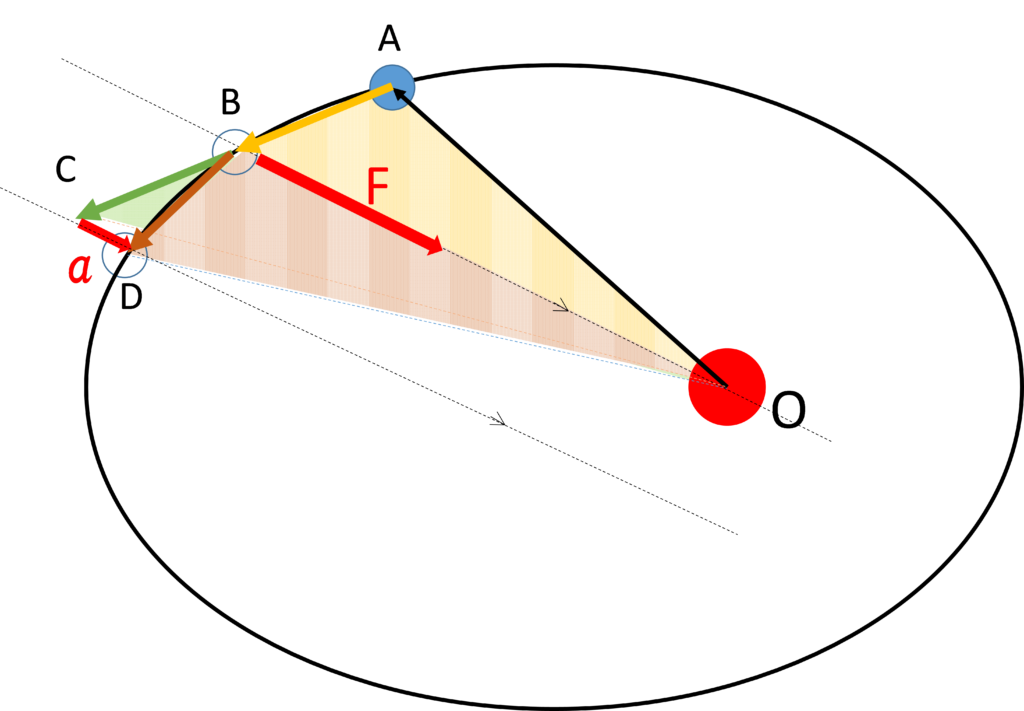
ゆえに、上図の $F$ と $a$ が平行のため三角形OBCと三角形OBDの面積は同じになります。
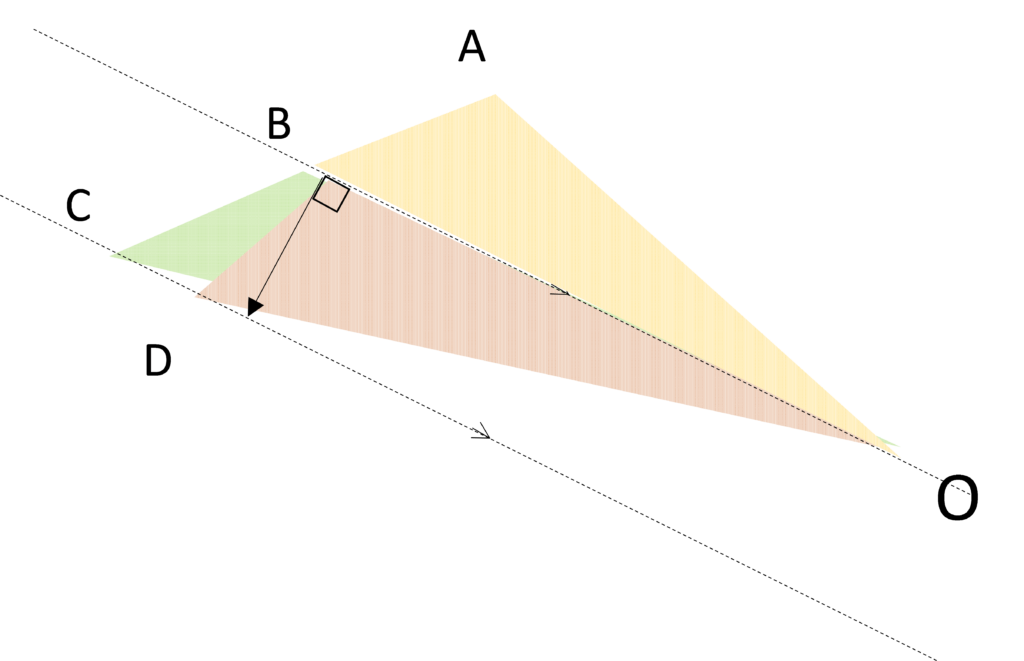
ということは、三角形OABと三角形OBDの面積も同じです。
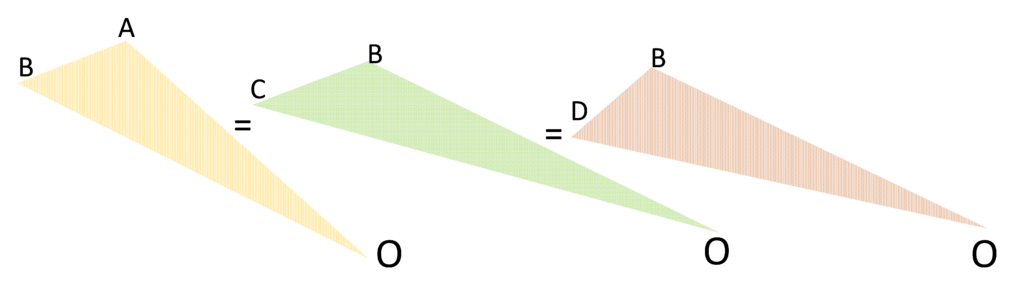
つまり、一定時間に惑星と太陽を結ぶ線が通過する面積が一定になっているのです。
これが面積速度一定の法則と呼ばれるものです。
ここで、もしもはたらく力が中心に向いていない場合は、OB と CD が平行でないため三角形OBCと三角形OBDの面積は同じになりません。

したがって、その様な場合には面積速度は一定にはなりません。
すなわち、回転中心に向く力によって運動している物体は面積速度が一定になるのです。
さて、この面積速度一定の法則についてもう少し考えましょう。次の図を見てください。
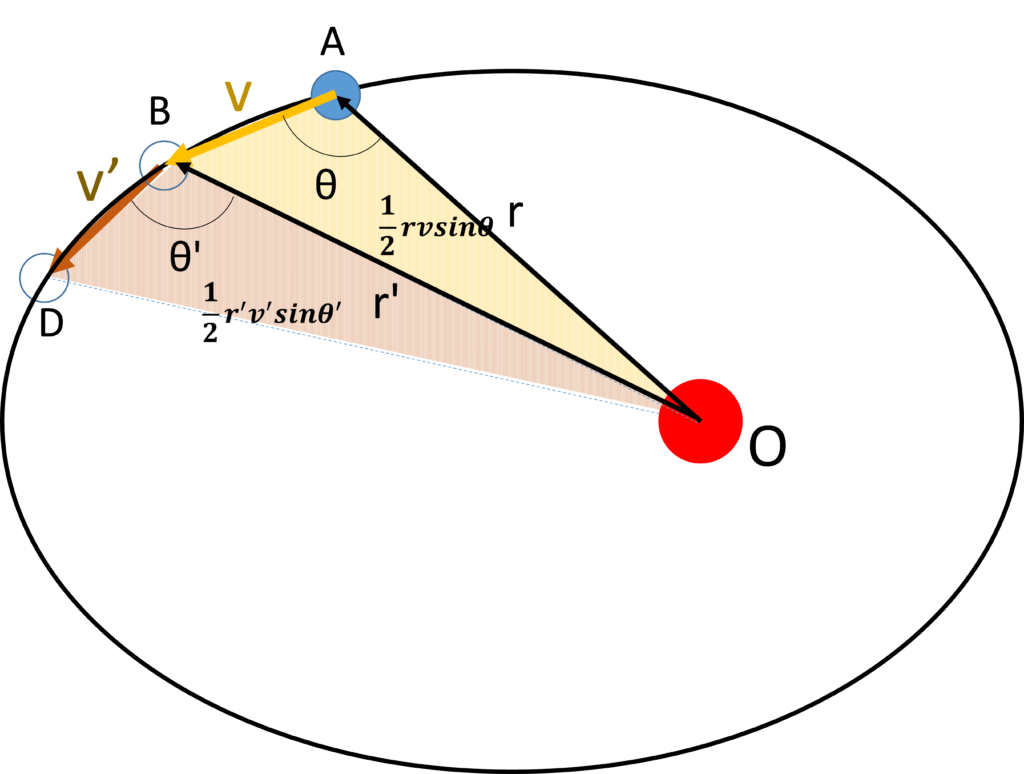
このとき三角形OABの面積は図の角度θとすると
$$\dfrac{1}{2}rv \sin\theta $$
としめされます。面積速度一定の法則から
$$\dfrac{1}{2}rv \sin\theta = \dfrac{1}{2}r^{\prime}v^{\prime} \sin\theta^{\prime} = C \:\:定数 $$
となるのは明らかです。
次に、この式の両辺に惑星質量 $m$ をかけて整理してみます。そうすると、定数を $C^{\prime}$ として次のように変形できます。
$$mvr\sin \theta =mv^{\prime}r^{\prime}\sin \theta^{\prime} = C^{\prime}$$
この等式は何を示すでしょうか? ご存知のように、$mv$ は運動量ですね。この $mv$ に $r \sin \theta $ を乗じたものが、中心に向かう力を受ける運動においては保存されているということになります。このとき、 $mvr \sin \theta$ を角運動量と呼びます。
これが角運動量保存法則です。
角運動量保存則
角運動量保存則は、
—————————————————————————————————
数学的にはベクトル積を使って次のように表すことができます。
$\vec{r}\times m \vec{v}= 一定$
—————————————————————————————————
ちなみに、力がはたらかないで等速直線運動する場合でも面積速度は一定に保たれますので角運動量も一定です)
こぼれ話
フィギィアスケートでは華麗なスピンが見られますね。
ところで、広げていた手を縮めると、不思議なことに回転の速さが増していきます。
これは角運動量保存の法則によるものです。
つまり手を伸ばした状態と縮めた状態での角運動量が保存されているため起こるのです。
先ほどの式を使って考えてみましょう。
$$mvr \sin\theta = mv^{\prime}r^{\prime} \sin\theta^{\prime}= C^{\prime} $$
において、$\theta=\theta^{\prime} =90° $ としてよいでしょうから、
$$mvr = mv^{\prime}r^{\prime} = C^{\prime} $$
です。 $m$ は同じですから、手を縮めた場合の速さ $v^{\prime}$ は
$$v^{\prime} =\dfrac{r}{r^{\prime}} v$$
となります。手を縮めて $ r^{\prime}< r $ であるなら、$v^{\prime} > v$ ですね。
これは回転いすを使えば簡単に実験できます。
まず、回転いすに腰掛けて回転させます。そのうえで伸ばしていた手や足を縮めると、明らかに回転が速くなることが実感できます。
手や足を伸ばすと今度は回転が遅くなります。








































コメント