コンデンサーの接続
コンデンサーを接続する場合大きく分けて並列接続と直列接続があります。
ここでは、それぞれについてその合成容量をもとめてみましょう。
また、あらかじめ充電されたコンデンサーの並列接続と直列接続について、勘違いやすい例をもとに解説していきます。
「並列・直列についてはよくわかっている」という人は、ここから読んでください。
並列
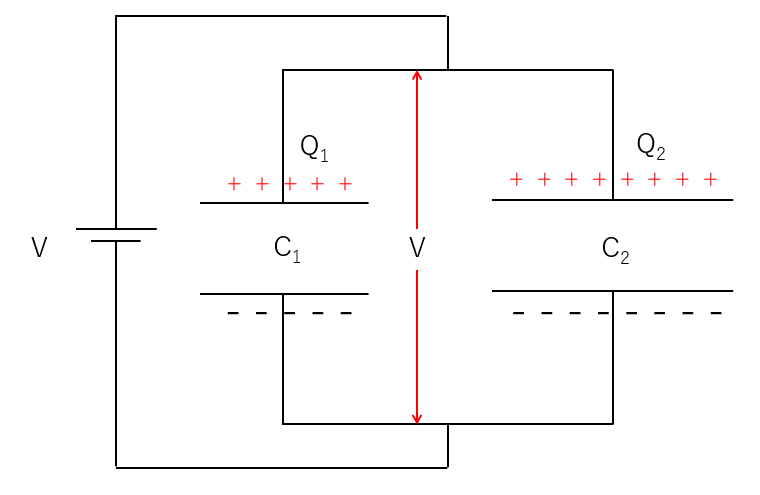
電気容量 $C_1$ と $C_2$ のコンデンサーを並列接続します。
コンデンサーの両端に電圧 $V$ を加えるときの各コンデンサーに蓄えられる電気量を求めてみます。
この場合、各コンデンサーにかかる電圧は必ず $V$ です。
$C_1$ のコンデンサーに蓄えられる電気量を $Q_1$ とすると、$Q=CV$ より、
$Q_1=C_1V$
同様に、$C_2$ のコンデンサーに蓄えられる電気量を $Q_2$ とすると、$Q=CV$ より、
$Q_2=C_2V$
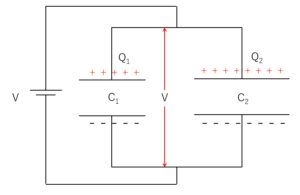
この、コンデンサー全体で蓄えられる電気量 $Q$ は、
$Q=Q_1+Q_2=C_1V+C_2V=(C_1+C_2)V$
なので、この時の合成容量 $C$ とすると、 $C=C_1+C_2$ となります。
一般に、コンデンサーが並列接続されている場合、その合成容量 $C$ は、
$C=C_1+C_2+\cdots \cdots +C_n$
で示されます。
直列
コンデンサー $C_1$、$C_2$ を直列接続する場合ですが、どのコンデンサーにも最初に電荷がないとします。
そうすると、コンデンサーの両端に電圧 $V$ を加えた場合、コンデンサーに最初に電荷がなければ、すべてのコンデンサーでは同じ電気量がたまります。
それはなぜでしょうか?
まず $C_1$ コンデンサーに電気量 $Q$ がたまる時を考えます。
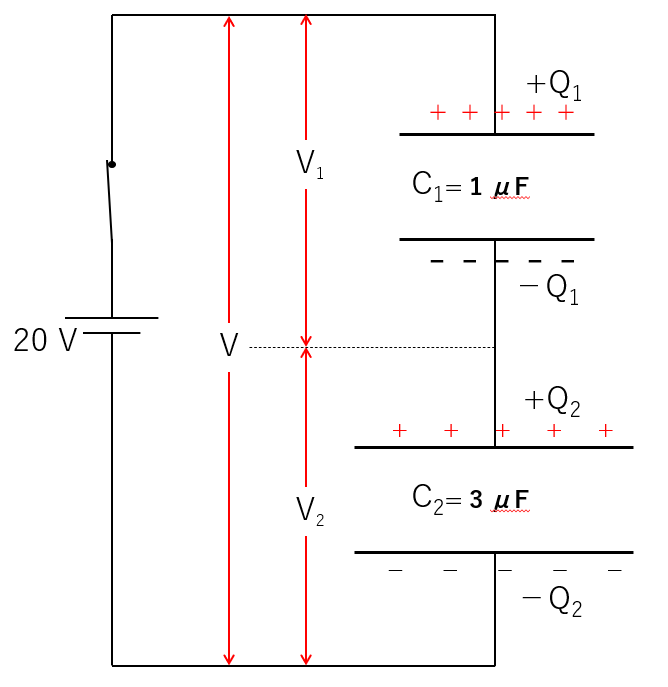
図のように、 $C_1$ コンデンサーの上側の極板には $+Q$ が貯まるとします。
そうすると、上の極板の $+Q$ に引かれて、下側の極板には $-Q$ がたまります。
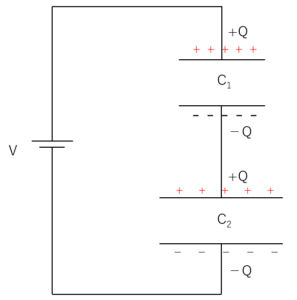
同様に、 $C_2$ コンデンサーの上の極板は $+Q$ の電荷がたまり、$C_2$ コンデンサーの下側の極板には $-Q$ の電荷がたまります。

これは、$C_1$ コンデンサーの下の極板と $C_2$ コンデンサーの上の極板は孤立しており、その電気量総和は、コンデンサーに最初に電荷がなければ、$0$ だからですね。

図の赤で囲った部分は孤立しています。
つまり、$(-Q)+Q=0$ ということですね。
各コンデンサーの極板間にかかる電圧を、それぞれ $V_1$、$V_2$ とすれば、 $V=\dfrac{Q}{C}$ より、
$V_1=\dfrac{Q}{C_1}$ $V_2=\dfrac{Q}{C_2}$
となります。

ここで、電圧の関係から $V=V_1+V_2$ ですから、合成容量を $C$ とすると、
$V=\dfrac{Q}{C_1}+\dfrac{Q}{C_2}$
$~~=\left( \dfrac{1}{C_1}+\dfrac{1}{C_2} \right)Q$
$~~=\dfrac{Q}{C}$
より、合成容量 $C$ は
$\dfrac{1}{C}=\dfrac{1}{C_1}+\dfrac{1}{C_2}$
となることがわかります。
したがって、直列接続したコンデンサーの合成容量 $C$ は
$\dfrac{1}{C}=\dfrac{1}{C_1}+\dfrac{1}{C_2}+\cdots \cdots +\dfrac{1}{C_n}$
で示されます。
注意すべき点
いくつか、具体的な例をあげてみます。
コンデンサーに最初に電荷がある場合
2つのコンデンサーを用意します。
電気容量をそれぞれ、コンデンサー $C_1=1\:\mu F$ 、 コンデンサー $C_2=3\:\mu F$ とします。
はじめに、それぞれのコンデンサーを $10\:V$ で充電しておきます。
その時の電気量をそれぞれ、 $Q_1$、$Q_2$ とすると、$Q=CV$ より
$Q_1=1\times 10=10\:\mu C$ $Q_2=3\times 10=30\:\mu C$
です。
そのうえで、これらのコンデンサーを並列・直列接続して $20\:V$ 電池に接続してみましょう。
並列
図のような組み合わせで並列接続します。
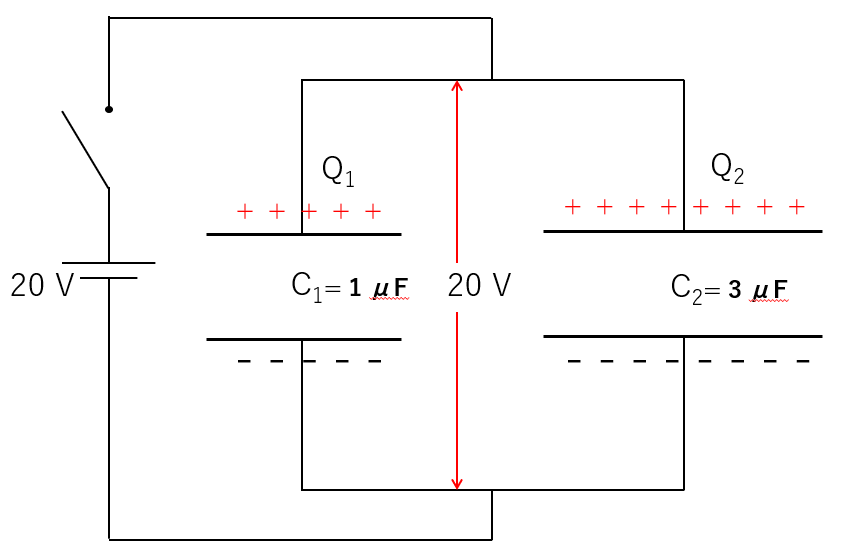
さて、並列接続した場合のコンデンサーにたまる電気量は?
これは当然ですが、図の並列接続では、コンデンサーにいくら充電されていようと、各コンデンサーの極板間電圧は $20\:V$ です。
したがって、$Q_1=C_1V=1\times 20=20 \:\mu C$ $Q_2=C_2V=3\times 20=60 \:\mu C$ です。
電気量総和は $Q=CV=(C_1+C_2)V=Q_1+Q_2=80\:\mu C$ となります。
コンデンサーを入れ替えて
では、図のような組み合わせはどうなるでしょうか?
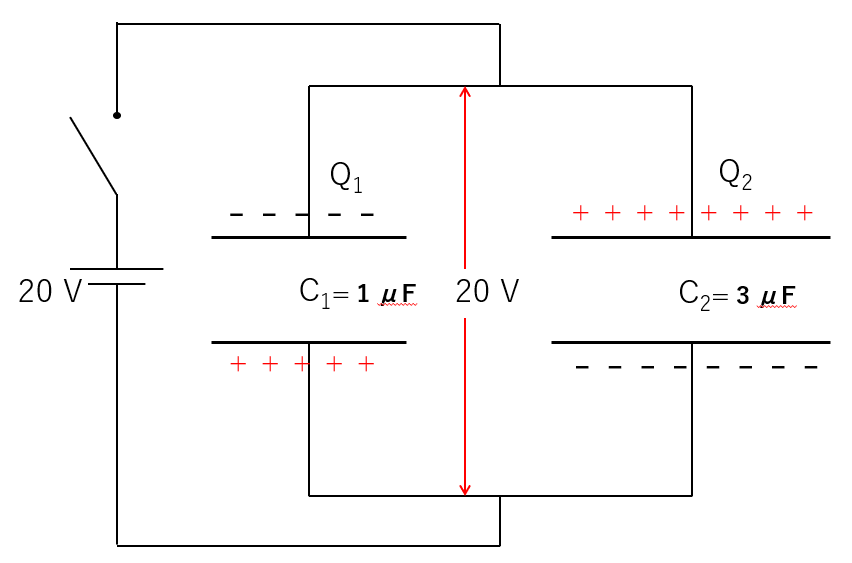
この場合も、同様に、電池に接続されている以上は各コンデンサーの極板間電圧は必ず $20\:V$ になります。
よって、結局どのようにコンデンサーをつないでも並列であれば、十分時間がたてば同じことです。
直列
基本的な解法
2つの充電されたコンデンサーを、図のように直列接続することにします。

さて、このとき「コンデンサーにたまる電気量はすべて同じ」・・・ではありません!
なぜなら、コンデンサーはすでに充電されているからです。
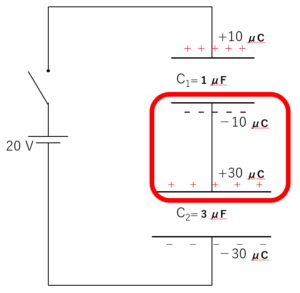
そこで、図のような電気量の分布になったと仮定します。
二つのコンデンサー間は電気的に孤立しているので、スイッチをつないだ後も電気総量は保存されます。図の赤で囲んだ部分です。
ここで、スイッチをつなぐ前には、2つのコンデンサー間の電気量総和は $-10+30\:\mu C$ であり、それはスイッチ接続後も変わらないことに注意します。
したがって、 $-10+30=-Q_1+Q_2$ が成り立ちます。電気量保存の法則
また、図の電圧 $V_1$、$V_2$ は、$V_1=\dfrac{Q_1}{C_1}$、 $V_2=\dfrac{Q_2}{C_2}$ です。

ここで、 $V=V_1+V_2$ なので、
$V=20=V_1+V_2=\dfrac{Q_1}{C_1}+\dfrac{Q_2}{C_2}$
です。すなわち
$20=\dfrac{Q_1}{1}+\dfrac{Q_2}{3}$
これと先ほどの、$-10+30=-Q_1+Q_2$ と連立させることで、$Q_1$ と $Q_2$ を求めます。
これより、$Q_1=10\:\mu C$ 、$Q_2=30 \:\mu C$ が得られます。
この場合にように、コンデンサーに最初に電荷がある場合は、直列のコンデンサーの合成容量の式は使えないことに注意しましょう。
電位法による解法
ついでに、この問題において、電位法による解法(物理のエッセンスの問題)をしてみましょう。
適当に、電位の基準を決めます。
わかりやすいように、そこをアースして $0\:V$ としましょう。
そして、2つのコンデンサーの間の電位を $x$ と仮定します。

このとき、
(正負も含めた自分の極板の電気量)=(電気容量)×(自分の電位ー相手の電位)
です。
電位法について、詳しくは
以下の問題を見てください。
よって、$-10+30=-Q_1+Q_2$ から、
$-10+30=-Q_1+Q_2=1\times (x-20)+3\times (x-0)$
が成り立つので、これより、$x=10 \:V$ です。
したがって、
$-Q_1=1\times (10-20)=-10\:\mu C$ より、$Q_1=10\:\mu C$
$+Q_2=3\times (10-0)=30 \:\mu C$
となります。
この解法は電位法と呼ばれていますが、式が一つで済むので簡単に解けるという利点があります。
基本的な解き方を理解・マスターしたうえで用いるようにしてください。
問題を解くうえで困ったとき・迷ったとき、頼れるのは基本です。
よろしければ、電位法に関しての物理のエッセンスの問題を解いてみましょう。


https://kokolainen.com/douga-essense-condenser32/
$ V)を決めます。次に電位を仮に $x$ と置いて、電荷保存から問題を解く方法です。非常にスピーディーに解を求めることができて便利です。エッセンスの次は良問、そして名問が...
この接続は並列か、直列か?
並列・直列問題です。

コンデンサー内へ金属板・誘電体を挿入
こちらも参考にしてください。

まとめ
コンデンサーの接続
並列接続
$C=C_1+C_2+\cdots \cdots +C_n$

直列接続
$\dfrac{1}{C}=\dfrac{1}{C_1}+\dfrac{1}{C_2}+\cdots \cdots +\dfrac{1}{C_n}$
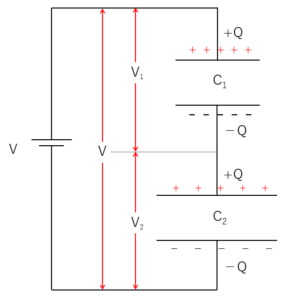
注意:各コンデンサーの最初の電荷は $0$ であること。



































コメント