コンデンサーの電気力線と電場および電位とそのグラフについて検討しましょう。
これらのグラフは意外と難しく、かつ盲点になりやすいと思います。
練習シートをダウンロードできます!
コンデンサーと電位・電場のグラフ
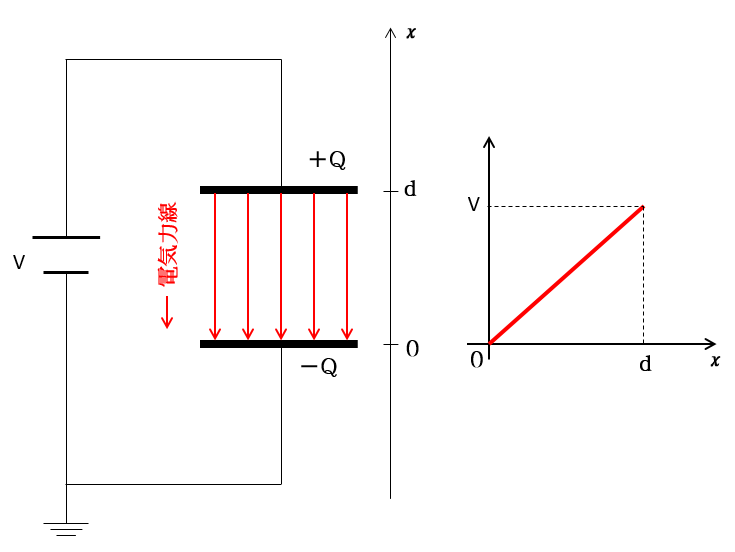
はじめに、コンデンサーを電圧 $V$ の電池に接続してフル充電します。
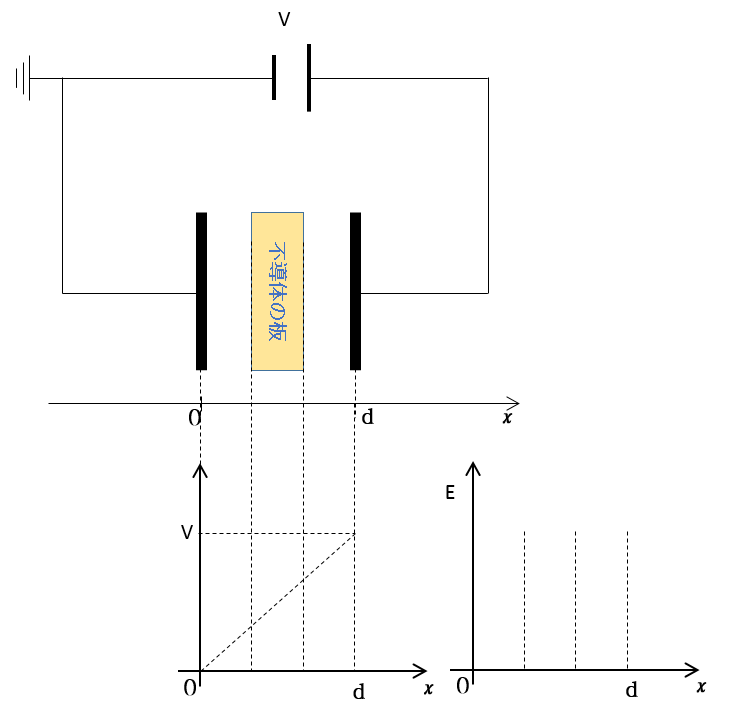
コンデンサーの極板に対して図のように $x$ 軸を取りましょう。
その場合の $x$ と極板間の電位差を示すグラフは図の右のようになります。
- その後電池を接続したまま、導体や不導体をコンデンサー内に挿入します。
- あるいは充電後、電池を切り離して同様の操作をした場合の電位のグラフについて考えます。
よりよくイメージするために、上の図を90度回転させてみます。
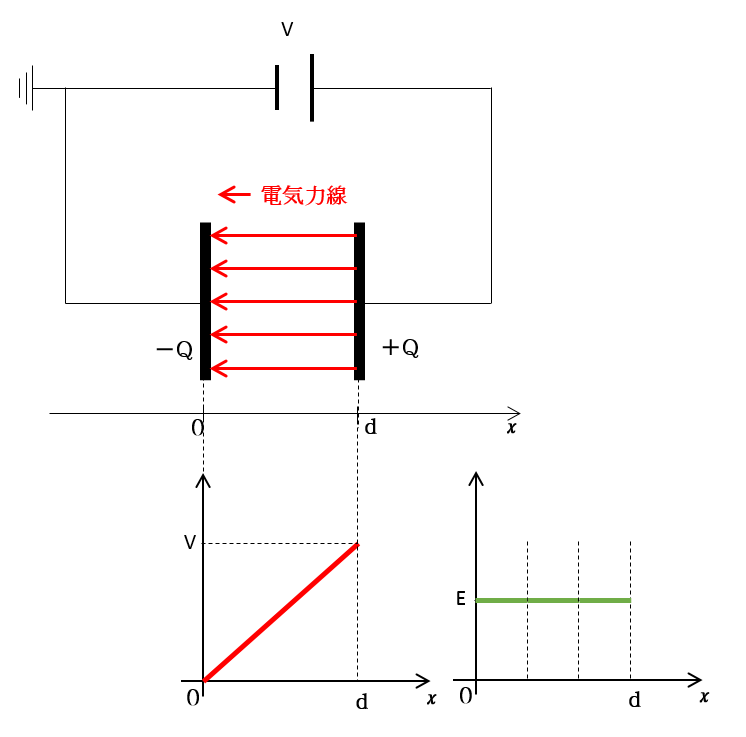
これで極板間隔とグラフの横軸が一致したので多少見やすくなったと思います。
電位グラフのとなりに電場 $E$ のグラフを追加しました。
このときのコンデンサーの極板間の電位差は $V$ で、電場の大きさを $E$ とします。
ではさっそく問題をやってみましょう。
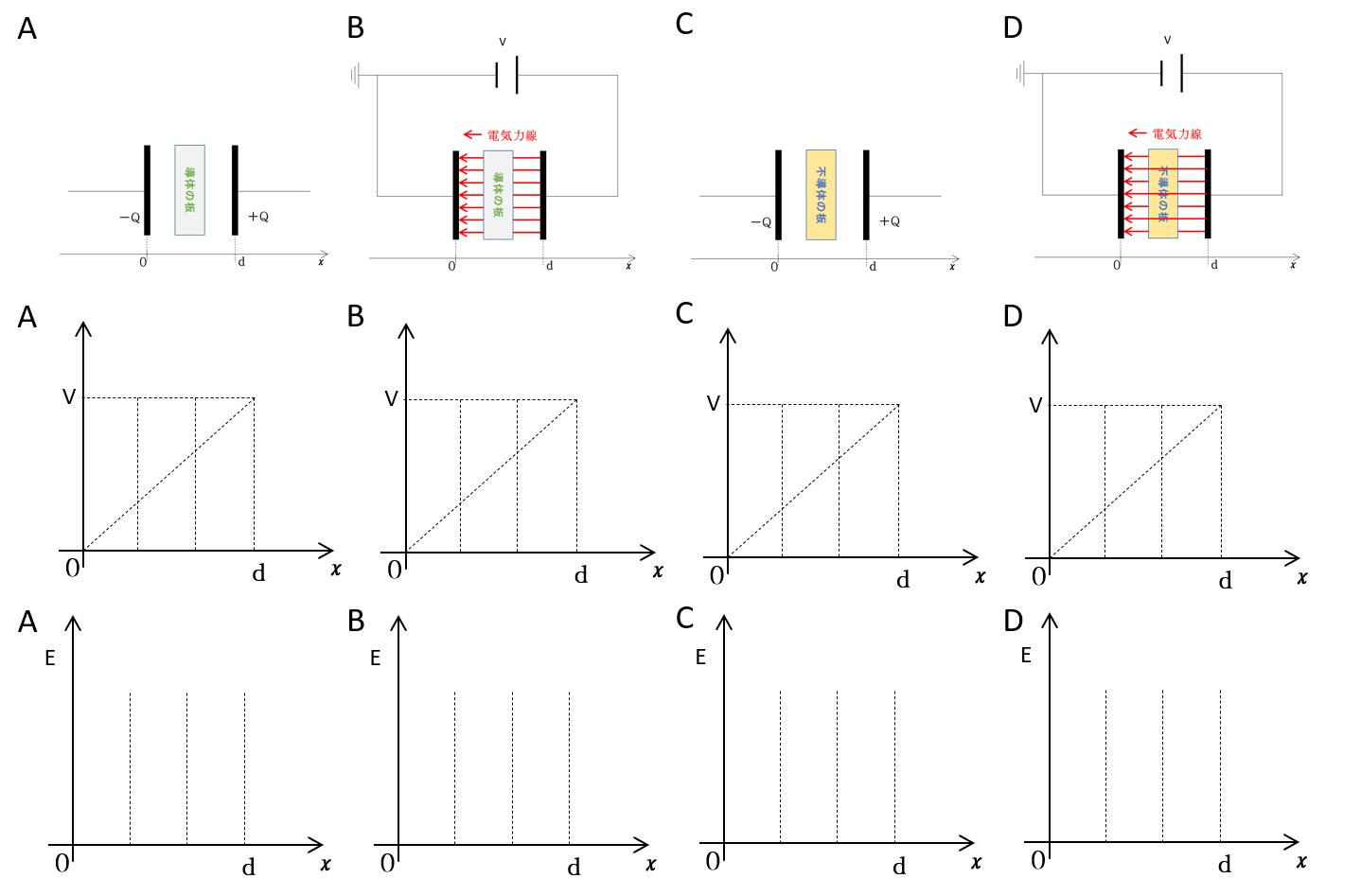
下の図は、今回扱う問題一覧です。
以下の問題では、すべてのコンデンサーの極板間隔を $d$ とし、挿入する導体・不導体の厚みを $\dfrac{d}{3}$ とします。
プリントはココからダウンロードできます。
コンデンサー内の電場と電位グラフ 練習シート
練習用シートをダウンロード・印刷すれば解答を直接描き込めます。
問題A 電池を切り離した状態で導体挿入
コンデンサーを電圧 $V$ でフル充電した後、次の図のように電池を切り離した状態で帯電していない導体板を挿入しました。
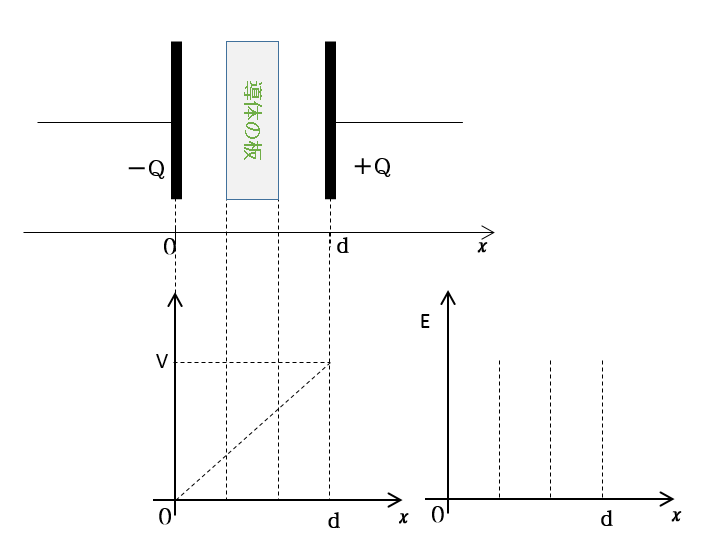
この場合の電位 $V$ と $x$ のグラフを描きましょう。
また、電場の大きさと $x$ との関係を示す概略のグラフを描きましょう。

問題A 解答
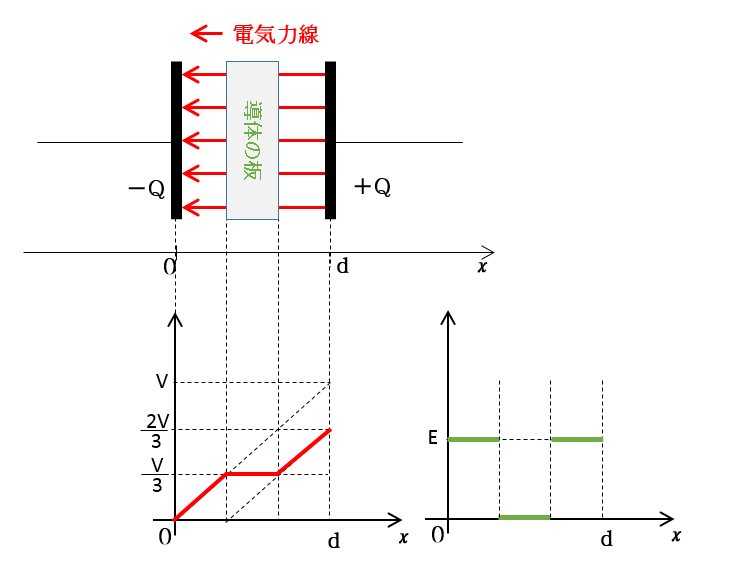

グラフの電場 $E$ の大きさは
コンデンサー内に何も入れないときと同じです。
電池を接続していないので、導体板を挿入した状態での極板間電圧は $V$ ではありません。
このとき極板上の電荷 $Q$ には変化がなく、導体を除くコンデンサー内の電場に変化はありません。
そのため、導体の挿入前後で電気力線の数に変化はありません。
また、導体内部にはやはり電気力線は入り込めません。
$\dfrac{1}{3}$ の厚みの導体を挿入したため、コンデンサーの極板間距離が $\dfrac{2}{3}$ になったのと同様です。
したがって、極板間の電圧は $\dfrac{2}{3}V$ です。

なぜって? 電位とは $+1\:[c\:]$ を運ぶ仕事ですからね!
電場が変わらないのに
極板間隔が短くなったので仕事は減ります。
これは、$V=Ed$ において、
$E$ が変わらず、$d$ が $\dfrac{2}{3}$ 倍になることからも明らかです。
あるいは、極板間電圧については $V=\dfrac{Q}{C}$ で考えてもいいでしょう。
電池が切り離されているため、導体板を挿入しても新たな電荷の供給はありません。
そのため、導体板を挿入してもコンデンサーの極板上の電荷 $Q$ は同じです。
$C=\epsilon \dfrac{S}{d}$ から考えます。
ここで、コンデンサーの極板面積の $S$ は変わっていません。
また、導体板を挿入すると $d$ が $\dfrac{2}{3}$ になるため、$C$ が $\dfrac{3}{2}$ 倍になります。
したがって、$V$ は $\dfrac{2}{3}$ 倍になる・・と考えても良いでしょう。
まとめると
- 導体内部では電場は0ですが、導体を除くコンデンサー内の電場の大きさはかわりません。
- 導体内部は等電位で電位の変化はなく、電位グラフの傾きは0です。
- 導体内部以外での電位グラフの傾きは導体の右と左側で同じで、このグラフの傾きは導体挿入前と変わりません。
- 導体をいれ、極板間距離が $\dfrac{2}{3}$ になったので、極板間電圧は $\dfrac{2}{3}V$ となります。


電位のグラフの傾きが
電場の大きさでしたね。
問題B 電池をつないだままで導体挿入
続いて、今度は電池を接続したまま、帯電していない導体板を挿入しました。
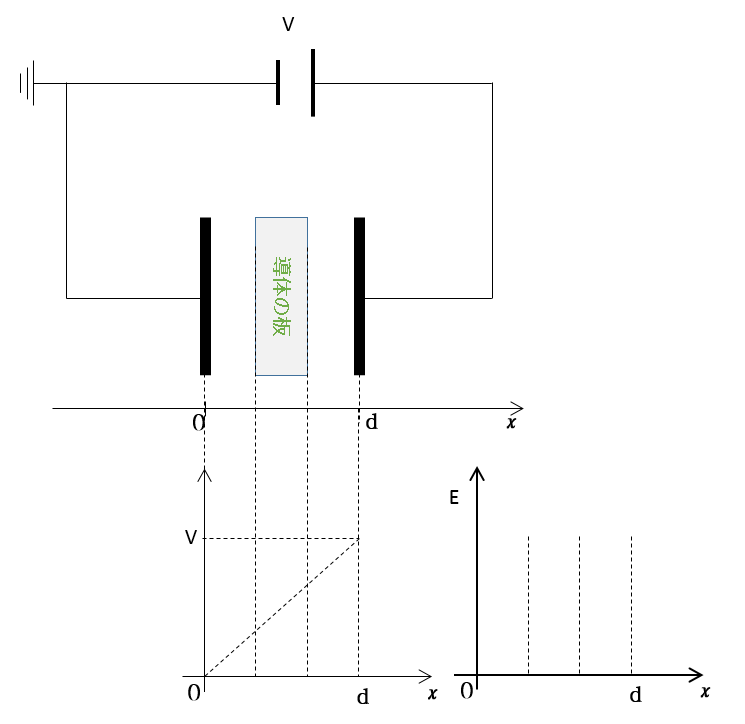
このとき、電位と $x$ のグラフを描きましょう。
また、電場の大きさと $x$ との関係を示す概略のグラフを描きましょう。

問題B 解答
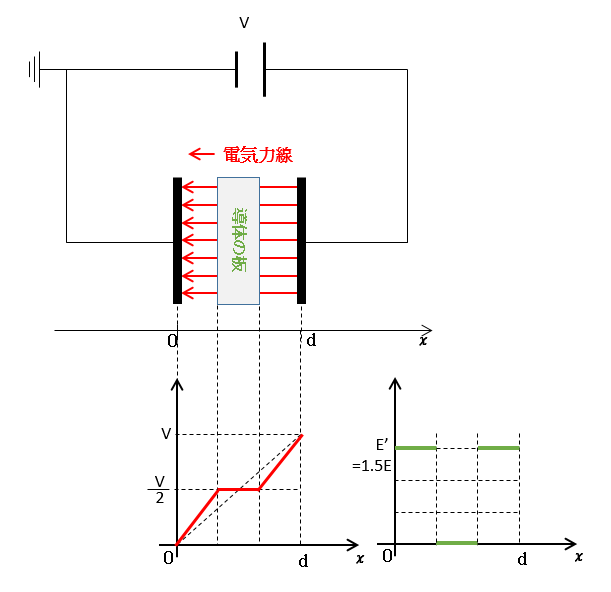

グラフの $E’$ の大きさはコンデンサー内に
何も入れないときの $E$ よりも大きくなります。
この問題の場合はグラフの傾き・あるいは
$E=\frac{V}{d}$ で $d \rightarrow \frac{2}{3}$
として $E’=1.5E$ です。
電池を接続したままなので、極板間電圧は $V$ です。

この場合、電池によりコンデンサーの
極板間電圧は $V$ が保証されます。
コンデンサー内部に導体を挿入するとコンデンサーの電気容量が大きくなります。
そのため、極板に貯まる電気量も増え、その結果、導体を除くコンデンサー内の電場は強くなります。(導体内部の電場はやはり0です)
そのため、導体の挿入後に電気力線の数は増加します。
また、導体内部にはやはり電気力線は入り込めません。
以上のことから、上のグラフのようになります。
電位グラフの傾きが電場の大きさを示すので、導体板の前後での電位グラフの傾きがともに大きくなっています。

電位のグラフの傾きが
電場の大きさでしたね。
まとめると
- 導体内部では電場は0ですが、導体を除くコンデンサー内の電場は大きくなります。(この問題では電位グラフの傾きは1.5倍なので 電場はコンデンサー内に何も入れないときの $E$ の1.5倍の大きさです)
- 導体内部は等電位で電位の変化はなく、電位グラフの傾きは0です。
- 電位グラフの傾きは導体の右と左側で同じで、この傾きは導体挿入前よりも大きくなります。
- 導体をいれても、電池に接続されているのでコンデンサーの極板間電圧は $V$ のままです。

問題C 電池を切り離した状態で不導体挿入
次の図のようにコンデンサーをフル充電した後、電池を切り離した状態で不導体板を挿入しました。
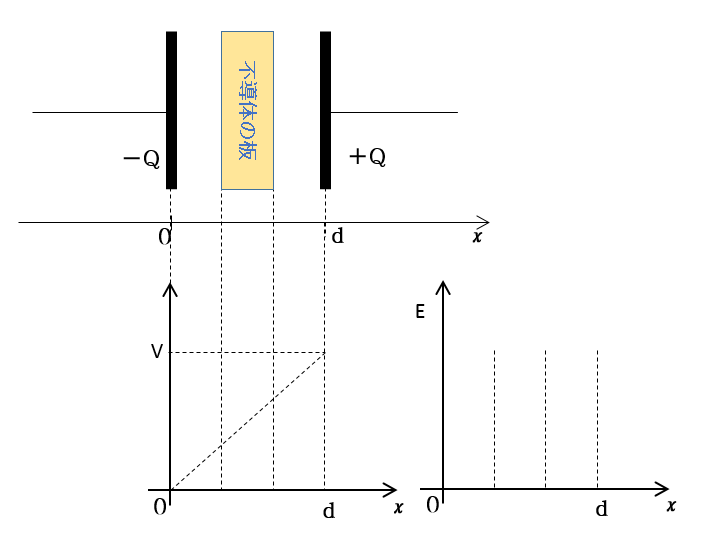
この場合の電位 $V$ と $x$ のグラフを描きましょう。
また、電場の大きさと $x$ との関係を示す概略のグラフを描きましょう。

問題C 解答


グラフの $E$ の大きさは
コンデンサー内に何も入れないときと同じです。
電池を接続していないので、コンデンサーの極板間電圧は下がります。
どれだけ下がるかは、不導体の比誘電率 $\epsilon_r$ で違います。($V=\dfrac{Q}{C}$, $C=\epsilon_0 \epsilon_r \dfrac{S}{d}$)
図では概略として不導体挿入後の電圧を $V’$ としています。
しかし、コンデンサーの極板にある電荷 $Q$ は変わらないので不導体以外の部分のコンデンサー内の電場は変化しません。
そのため、不導体の挿入前後で電気力線の数に変化はありません。(不導体内部では電気力線は減少します)
電圧のグラフを描くと不導体挿入前と挿入後で、不導体を含まないコンデンサー内の電位グラフの傾きは同じです。
不導体内部での電場も0ではないため、不導体内部の電位グラフもある傾きを持ちます(不導体内も電位差があります)。
まとめると
- 不導体内部では電場は0ではありません。不導体を含まないコンデンサー内の電場は不導体挿入前と同じです。
- 不導体内部は電位の変化があります。電位グラフはゆるい傾きをもちます。
- 電位グラフの傾きは不導体の右と左側のコンデンサー内では同じで、この傾きは不導体挿入前と同じです。
- 不導体をいれるとコンデンサーの極板間電圧はさがります。下がり方は不導体の比誘電率によります。

問題D 電池をつないだままで不導体挿入
続いて、今度は電池を接続したまま不導体板を挿入しました。
この場合の電位 $V$ と $x$ のグラフを描きましょう。
また、電場の大きさと $x$ との関係を示す概略のグラフを描きましょう。

問題D 解答
電池を接続したままなので、極板間電圧は $V$ です。

この場合、電池によりコンデンサーの
極板間電圧は $V$ が保証されます。
コンデンサー内部に不導体を挿入するとコンデンサーの電気容量が大きくなります。
不導体内部にも電場が存在し、その電位には傾きが生じます。
そのため、極板に貯まる電気量も増え電場は強くなります。
ゆえに、不導体の挿入後に電気力線の数は増加します。(不導体内部にも電気力線は存在します)

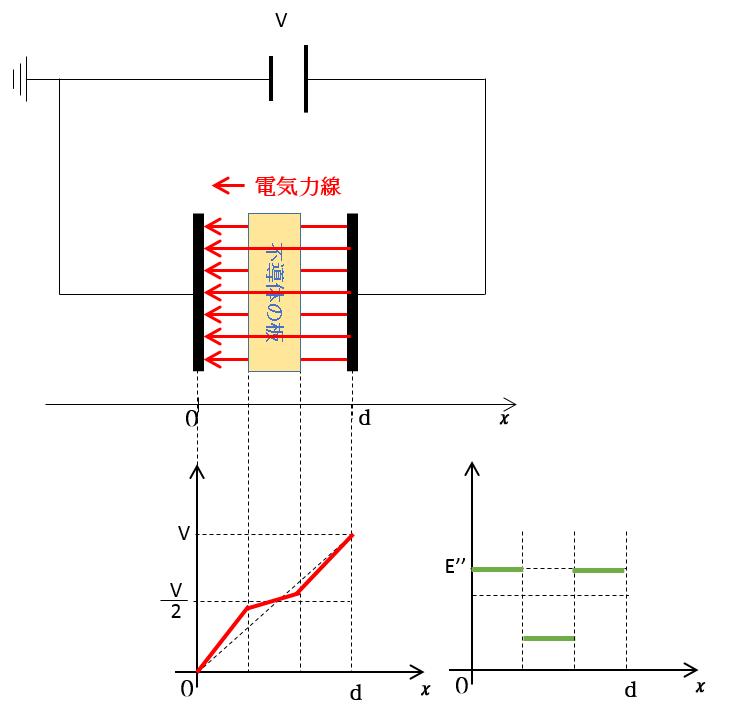
グラフの電場 $E”$ の大きさはコンデンサー内に
何も入れないときの $E$ よりも大きくなります。
なぜかというとコンデンサーの電気容量が増加するために
極板に貯まる電気量が増えるからですね。
そうると電気力線も増加します。
以上のことから、上のグラフのような電位・電場になります。
電位グラフの傾きが電場の大きさを示すので、不導体板の前後での電位グラフの傾きがともに大きくなっています。

電位のグラフの傾きが
電場の大きさでしたね。
まとめると
- 不導体内部では電場は0ではありません。不導体以外の部分の電場は大きくなります。
- 不導体内部は電位が変化し、その電位グラフはゆるやかな傾きを持ちます。
- 電位グラフの傾きは不導体の右と左側で同じで、この傾きは不導体挿入前よりも大きくなります。
- 不導体をいれても、電池に接続されているのでコンデンサーの極板間電圧は $V$ のままです。

全部まとめると
プリントはココからダウンロードできます。 コンデンサー内の電場と電位グラフ 練習シート
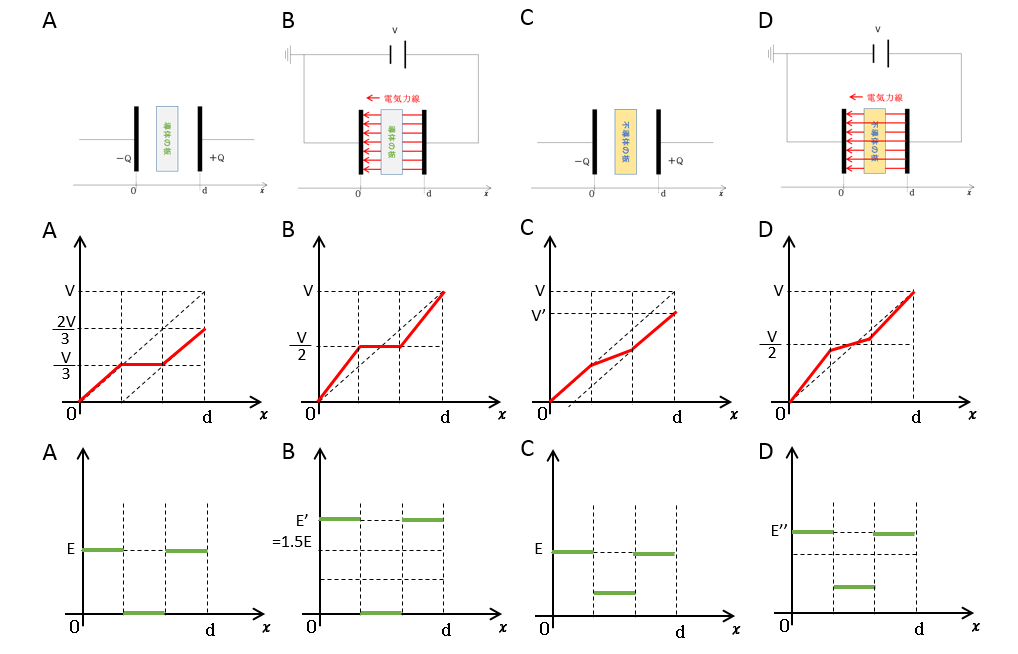
電場 $E$ の大きさ等に関しては目安です

よろしければ YouTube チャンネル登録もお願いします!
こちらも参考にしてください。




































コメント