
geralt / Pixabay
波の式解説
波の式は一般に、
ある時刻 t のとき、原点から x だけはなれた位置での変位 y を知りたいというものです。
なので、$y = f(x,t) $ というような関数になります。
つまり、波の式が難しいと感じるのは、変数が( x , t ) という二つの変数が存在するからなのです。
高校数学での sin や cos 関数などは基本的にはそういう問題はありません。
$y=f(x)$ で示されるものがほとんどす。
つまり、時間とともにグラフがくねくねと動いていくということを想定していません。
ある時刻 t で描かれた波のグラフは、移動している波のある一瞬を描きとめたものになるのです。まずこのことをイメージできるようにしてほしいですね。
波の y-x を描いた瞬間にそのグラフはその時刻専用のグラフになるのです。
以下のビデオでは波の式の作り方やその考え方を解説しています。
1.5倍速程度が見やすくてよいと思います。
波動において波の式というのは意外と後回しにしがちなところですね。
波の式はちょっとわかりづらいらしくて放置してしまっている人も多く見かけますが、一度しっかり取り組んで理解してしまいましょう。
そうすれば、後はその応用ということになります。
とにかく、しっかり理解するまでがんばってくださいね!
定常波と波の式についてはこちらをご覧ください。
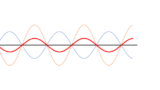
左右から振幅だけが違う波を合成しても定常波はできない!
定常波は振幅、波長、周期、波の速さが全く同じ波が一直線上・左右からぶつかる時に生じます。 しかし、波長、周期(波の速さ)が全く同じで、振幅だけが違う波が一直線上左右からぶつかる場合、合成波は移動していくように見えます。






































コメント