電池の起電力と内部抵抗
電池といえども、その内部に抵抗が存在します。
これが電池の内部抵抗です。
図では $r$ で示しています。
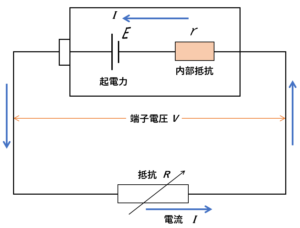
したがって、回路に電流 $I$ を流すと、電池内部では内部抵抗 $r$ による電圧降下 $rI$ が生じます。
このとき電池の両端で測定される電圧 $V$ を電池の端子電圧といいます。
また、内部抵抗の電圧降下によらない、電池本来の電圧というものが定義され、これを $E$ とし、起電力と呼びます。
つまり、電池に電流 $I$ を流すと、電池の両端では、電池本来の電圧(起電力)から内部抵抗による電圧降下 $rI$ 分だけ電圧が下がるので、
$V=E-rI$
となります。
あるいは次のように考えてもいいでしょう。
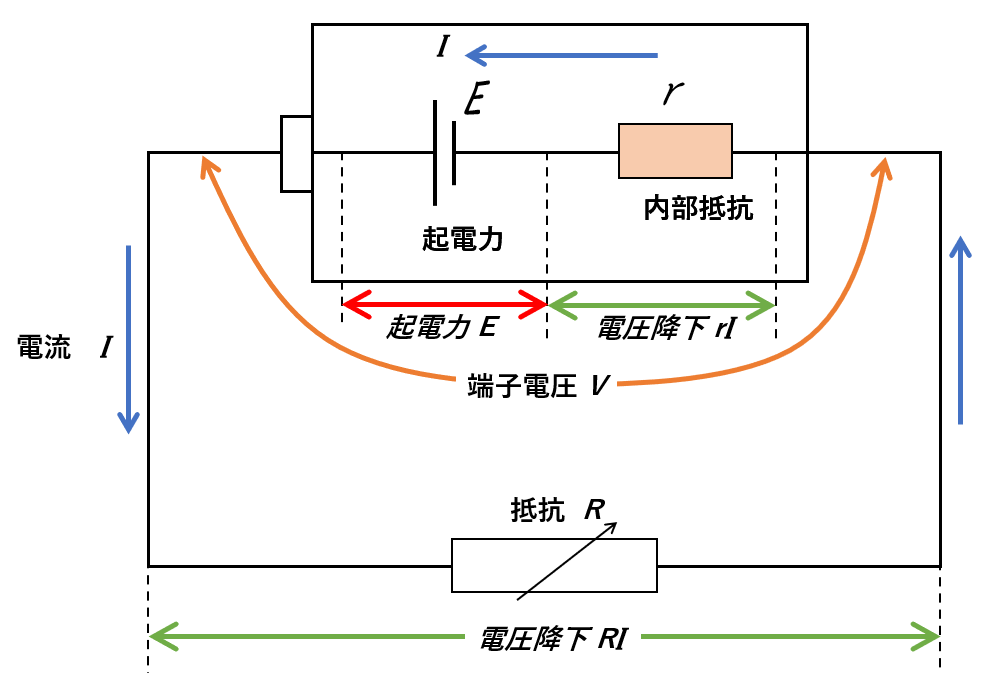
図においてキルヒホッフの法則から
$E=rI+RI$
ここで、端子電圧 $V$ と可変抵抗での電圧降下 $RI$ は等しく、 $V=RI$ だから、
\begin{eqnarray}
E&=&rI+RI\\\\
E&=&rI+V\\\\
V&=&E-rI
\end{eqnarray}
となり、当然ですが、同じ結果になります。
次に、先ほどの結果、$V=E-rI$ の $I-V$ グラフを描いてみると
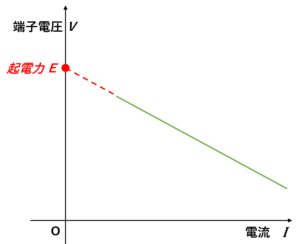
のようになり、電池に流れる電流 $I$ が $0$ であるなら、
$V=E-r\times 0=E$
となり、電池の起電力 $E$ とは電流の流れていないときの端子電圧 $V$ ということになります。
電池の起電力を正確に知りたいときには、電位差計というものを用いて測定することが可能です。
電位差計については以下の記事を参照してください。


回路の消費電力

図の回路において、外部抵抗が可変であるとき、外部抵抗での消費電力 $P$ を最大にする外部抵抗値 $R$ を求めます。
回路を流れる電流 $I$ は、キルヒホッフの法則より
$E=rI+RI$
であるので、
$I=\dfrac{E}{R+r}$
と示されます。
抵抗 $R$ での消費電力 $P$ については、$P=IV=I^2R=\dfrac{V^2}{R}$ から、$P=I^2R$ の式を使い、先ほど求めた $I$ を代入すると、
\begin{eqnarray}
P&=&I^2R\\\\
&=&\left( \dfrac{E}{R+r} \right)^2R\\\\
&=&\dfrac{E^2R}{(R+r)^2}\\\\
&=&\dfrac{E^2}{\frac{(R+r)^2}{R}}\\\\
&=&\dfrac{E^2}{\frac{(R+r)^2}{\sqrt{R}\,^2}}\\\\
&=&\dfrac{E^2}{\left( \frac{R+r}{\sqrt{R}} \right)^2}\\\\
&=&\dfrac{E^2}{\left( \sqrt{R}+\dfrac{r}{\sqrt{R}} \right) ^2}\\\\
\end{eqnarray}
ここで、$P$ を最大にするには、$\left( \sqrt{R}+\dfrac{r}{\sqrt{R}}\right)$ を最小にすればよいことになります。
したがって、相加相乗平均を使って、$(R>0,\:r>0)$
$\left( \sqrt{R}+\dfrac{r}{\sqrt{R}} \right) \geqq 2\sqrt{\sqrt{R}\dfrac{r}{\sqrt{R}}}$
等号は、$\sqrt{R}=\dfrac{r}{\sqrt{R}}$ となります。
よって可変抵抗 $R$ での消費電力を最大にする条件は、$R=r$ のときです。





































コメント