物理のエッセンス 力学 97番について解説します。
ばねを任意の長さに切ったときのばね定数についても解説しています。
物理のエッセンス 力学 97番 P83
ばね定数 $k$ のばねの両端に質量 $m$ の球をとりつけて振動させるときの振動周期を求める、という問題です。
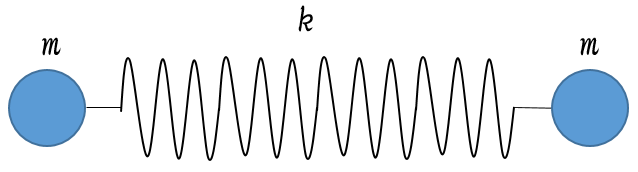
この問題はばねを2つに分けて考えるとわかりやすいと思います。
考えよう
ばねの合成定数で示したように、ばねを半分に切るとばね定数は2倍になります。
この場合、ばねの両端に取り付けた球の質量は同じなので、両方に引っ張って同時に離したとき、振動の中心は2球間のちょうど真ん中になります。つまり重心位置になります。
つまりばねの真ん中が不動点となり、全体が振動すると考えられます。

そうすると、ここでばねの半分だけに注目すると、ばね定数 $2k$ のばねに質量 $m$ の球がついて単振動していると考えて差し支えないわけです。

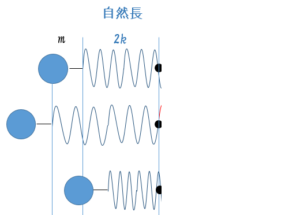
ということは、単振動の周期の式 $T=2\pi\sqrt{\dfrac{m}{K}}$ より、$K=2k$ として、
$$T=2\pi\sqrt{\dfrac{m}{2k}}$$
となります。
ここで、ばねにもう一度目を向けてみると、ばねは右半分と左半分に分けましたが、ばね全体としては単純に伸びたり縮んだりしているだけですから、右半分のばねが一番縮むということはばね全体でも一番縮んていると考えることができます。
したがって、全体でも周期は同じく $T=2\pi\sqrt{\dfrac{m}{2k}}$ となります。
球の質量が違った場合でも重心は不動であることを考えて同様に解くことができます。
球の質量が違っている場合について
球の質量が違っている場合について考えてみます。

重心のそれぞれの球からの距離は、ばねの長さを $l$ とすると、それぞれの質量の逆比に内分するので、
$\dfrac{ml}{M+m}$ $\dfrac{Ml}{M+m}$
です。(図)
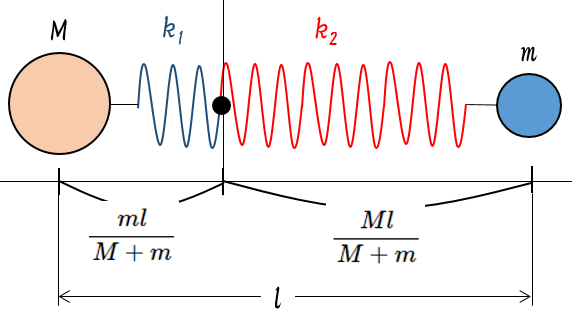
ここで、この重心を不動点と考えます。
この場合のばね定数は、図の左を $k_1$、右を $k_2$ とすれば、
$k_1=\dfrac{1}{\frac{\frac{ml}{M+m}}{l}}\times k=\dfrac{M+m}{m}k$
$k_2=\dfrac{1}{\frac{\frac{Ml}{M+m}}{l}}\times k=\dfrac{M+m}{M}k$
となります。なぜそうなるかは、短くした場合のばね定数の計算方法を見てください。
ということは、質量 $M$ の球について、単振動の周期の式 $T=2\pi\sqrt{\dfrac{m}{K}}$ より、$m\rightarrow M$、$K=k_1$ として、
\begin{eqnarray}
T&=&2\pi\sqrt{\dfrac{M}{k_1}}\\\\
&=&2\pi\sqrt{\dfrac{M}{\frac{M+m}{m}k}}\\\\
&=&2\pi\sqrt{\dfrac{mM}{(M+m)k}}
\end{eqnarray}
となります。
あるいは、質量 $m$ の球について、$m\rightarrow m$、$K=k_2$ として、
\begin{eqnarray}
T&=&2\pi\sqrt{\dfrac{m}{k_2}}\\\\
&=&2\pi\sqrt{\dfrac{m}{\frac{M+m}{M}k}}\\\\
&=&2\pi\sqrt{\dfrac{mM}{(M+m)k}}
\end{eqnarray}
どちらにしろ同じになることがわかります。
つまりどちらで考えても周期は同じです。
これは先程と同じように、ばね全体についてばねだけの運動を考えるとばね全体の振動周期だから同じ・・・というのがわかると思います。
短くした場合のばね定数の計算方法
ばねを任意の長さに短くしたときのばね定数について考えます。
ばね定数は、その長さに反比例します。
$x\times k=C$、つまり、長さ×ばね定数=一定 といえます。

たとえば、長さ $x$ ばね定数 $k$ のばねの長さを $\frac{1}{3}$ にしてみる。
そうすると、新しいばね定数 $k’$ は $k’=3k$ となるはずですね。
長さ×ばね定数=一定 ですから、
$x\times k=C$
長さを $\frac{1}{3}$ にした場合も同様に、
$\dfrac{x}{3}\times k’=C$
これらを片々割ります。
$\dfrac{\frac{x}{3}\times k’}{x\times k}=\dfrac{C}{C}=1$
つまり、ばね定数は $k’=\dfrac{1}{\dfrac{\frac{x}{3}}{x}}\times k$ という計算式が成り立ちます。






































コメント