物理のエッセンス 力学 99番 P85
問題
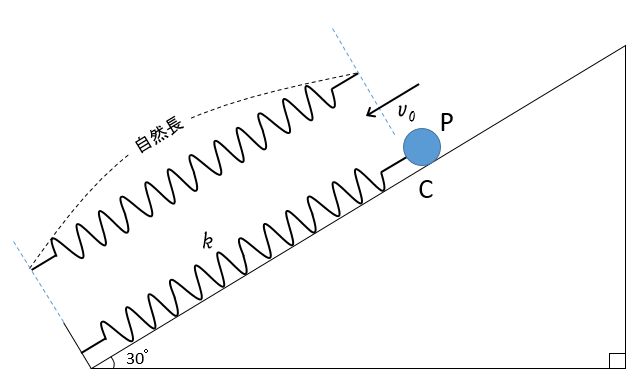
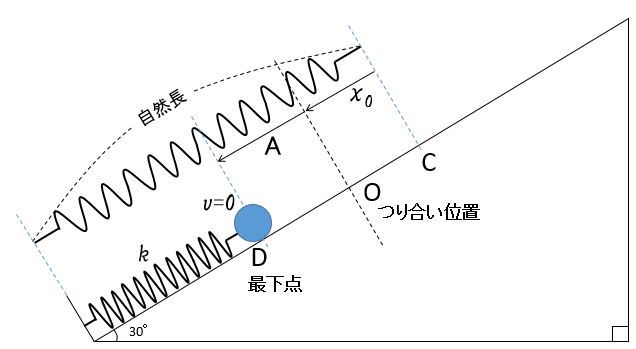
斜面上に置かれた球とばねが連結されている。
最初、ばねの自然長の位置で球に初速度 $v_0$ を図のように斜面下向きに与える。
このときの単振動の振幅を求めるという問題です。
考え方
まずつり合い位置での力の関係を調べます。
ばねの問題ではお約束ですね。
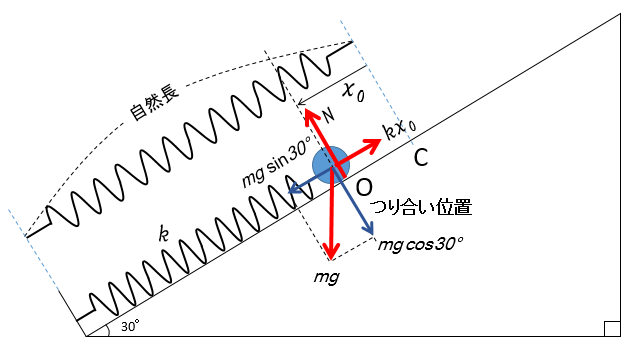
図より、
$$mg\sin 30^{\circ}=kx_0$$
よって、
$$x_0=\dfrac{mg}{k}\sin 30^{\circ}=\dfrac{mg}{2k}\:\:\cdots(a)$$
さてこのとき、解法には2種類あります。
力学的エネルギー保存則を使う方法と単振動エネルギーを考える方法です。
この記事が参考になります。まだマスターできていない人は必ずこの記事を理解しておいてください。

力学的エネルギー保存則を考える方法
まず一つ目の方法として、力学的エネルギー保存則を用いる方法について解説します。
この記事を参考に。
図の最下点を重力による位置エネルギーの基準とします。
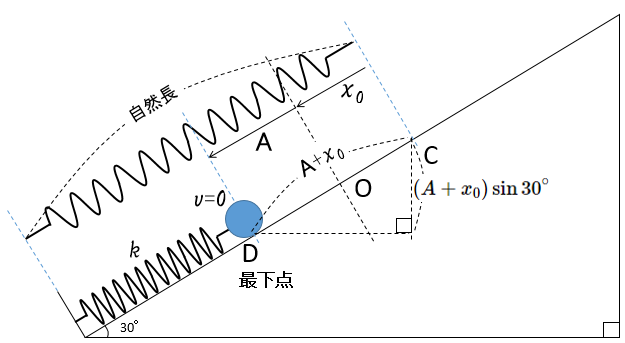
そうすると、
力学的エネルギー=(重力による位置エネルギー+ばねの位置エネルギー)+運動エネルギー
として示されますから、図の C と D の位置についてエネルギー保存の式を立てましょう。
最下点では 球の速さ=0 であることを考えて、
\begin{eqnarray}
\left(mg(A+x_0)\sin 30^{\circ}+\dfrac{1}{2}k\!\cdot \!0^2\right)+\dfrac{1}{2}mv^2_0=\left(mg\!\cdot \!0+\dfrac{1}{2}k(A+x_0)^2\right)+\dfrac{1}{2}m\!\cdot \!0^2
\end{eqnarray}
となります。ここで式 $(a)$ を使って答えを出します。
ここでは具体的な計算をひとまず置いておいて、次の方法を考えてみましょう。
単振動エネルギーを考える方法
単振動エネルギー保存則を使う方法はこの記事で詳しく解説していますので参考にしてください。
ここで重要なことは単振動の振動中心はどこか? ということです。
以前の記事を読んでいただけた方はよくおわかりと思いますが、振動中心はつり合い位置です。
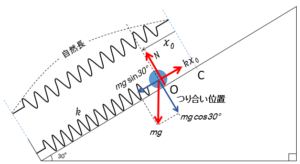
したがって、図の位置 $O$ を中心として振幅 $A$ で単振動する、ということになります。
さて、単振動エネルギーというのは、この振動中心からの変位 $x$ を使って、$\dfrac{1}{2}kx^2+\dfrac{1}{2}mv^2=一定$ であることを利用するものです。
ということは初期位置 C と最下点 D について、エネルギーを考えます。
つまり、
$$\dfrac{1}{2}kx^2_0+\dfrac{1}{2}mv^2_0=\dfrac{1}{2}kA^2$$
が成立します。
したがって、これと式 $x_0=\dfrac{mg}{2k}\cdots(a)$ より、
\begin{eqnarray}
A&=&\sqrt{x^2_0+\dfrac{mv^2_0}{k}}\\\\
&=&\sqrt{\dfrac{m^2g^2}{4k^2}+\dfrac{mv^2_0}{k}}
\end{eqnarray}
どうでしょうか?こちらのほうが劇的に簡単にできることがわかります。
補足 なぜ重力の位置エネルギーを考えなくてもよいのか
なぜ重力の位置エネルギーを考えなくてもよいのでしょうか?
以下の記事で詳しく解説しています。ご参考にしてください。

















コメント